1  Introduction to Calculus

Calculus (Mathematical Techniques) is a branch of mathematics that helps us understand how things change (such as population growth, temperature rise, or production rates) and how things move (like a car on the road, an object falling, or material flowing in a system). It provides useful tools to solve problems, make predictions, and create models in science, engineering, and daily life. In Mining whether in oil, coal, gold, copper, or other mineral resources—calculus is applied to estimate reserves, calculate safe and efficient extraction methods, model slope stability, predict groundwater flow, monitor production performance, and optimize operational aspects such as cost efficiency, revenue generation, and workforce allocation. In Metallurgy, it is used to analyze heating and cooling processes, optimize smelting operations, study chemical reaction rates, design stronger alloys, and predict corrosion over time. Overall, calculus is not just about numbers but a practical tool that supports efficiency, safety, and sustainability in industries such as mining, metallurgy, and many other fields.

1.1 Overview

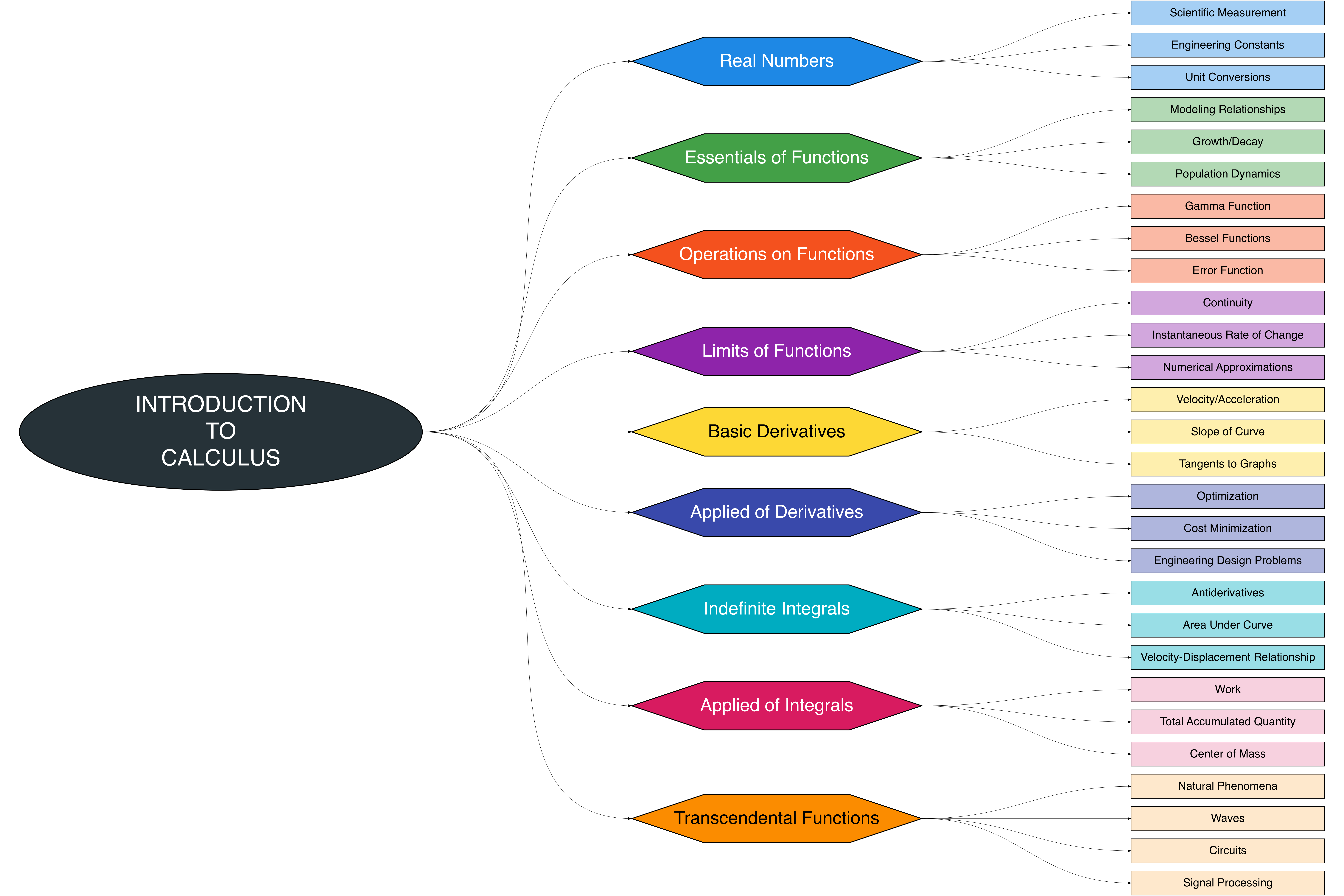
The Figure 1.1 presents a visual overview of the chapter, highlighting the structure of key topics and their interconnections. It provides readers with a clear guide to navigate the material and understand ho w concepts link to applications.

Figure 1.1: Mind Map of Introduction to Calculus

This chapter introduces the fundamental building blocks of calculus, including real numbers, functions, limits, derivatives, integrals, and transcendental functions. Each concept is connected to practical applications to illustrate how calculus underpins real-world problem-solving.

1.2 Applied Calculus

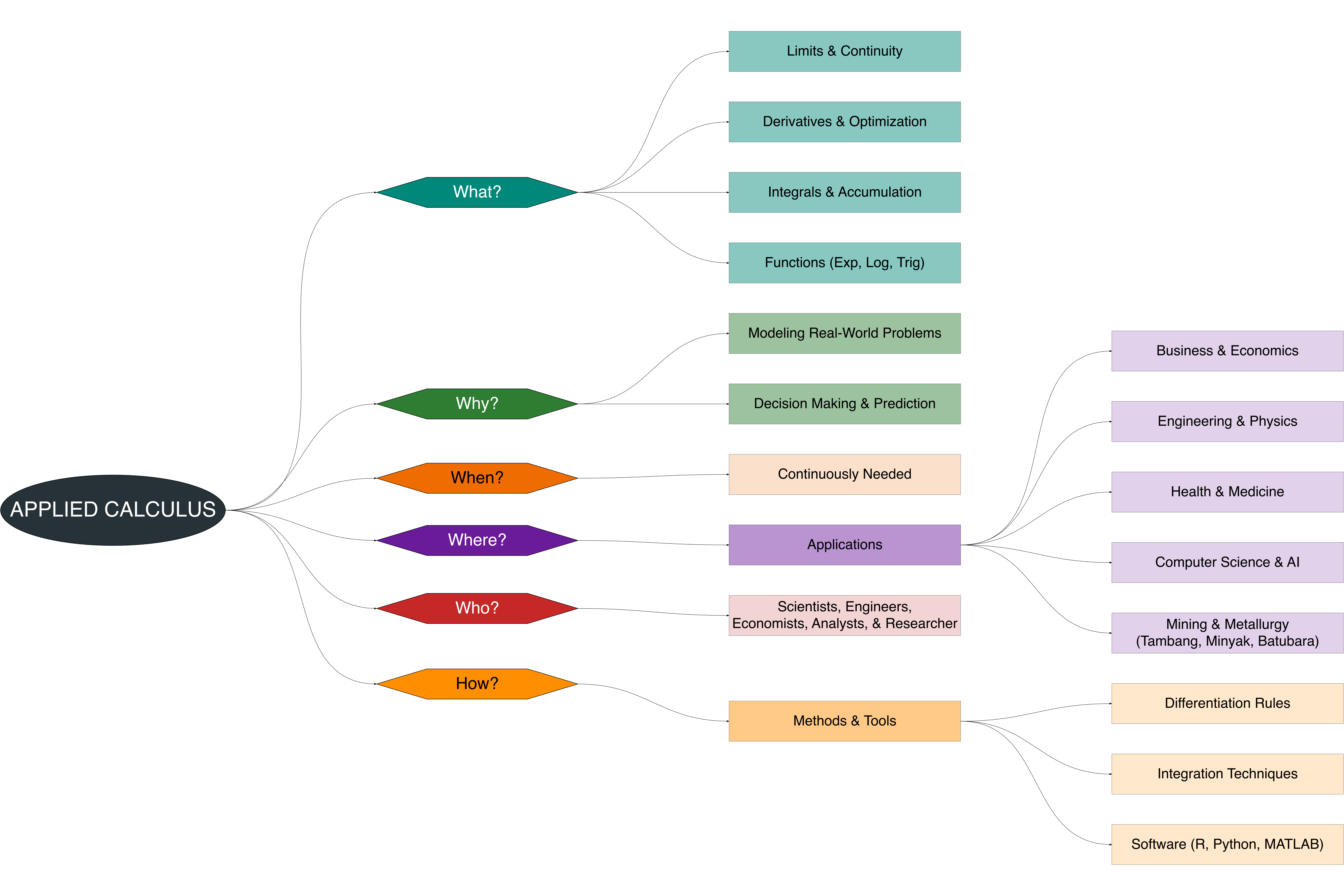
Applied Calculus (Figure 1.2) is a branch of calculus that focuses on the practical application of limits, derivatives, integrals, and special functions in solving real-world problems. Rather than being studied purely as a theoretical subject, calculus is presented here as an analytical tool to understand change, model phenomena, and support decision-making across multiple disciplines.

Figure 1.2: Detailed 5W+1H for Applied Calculus

The following mindmap illustrates a 5W+1H framework that explains:

  • What: The core concepts of Applied Calculus, including limits, derivatives, integrals, and special functions.
  • Why: Its importance in modeling real-world problems, prediction, and decision-making.
  • When: Applied Calculus has always been important in the past, remains essential today, and will continue to be needed in the future for science, technology, and real-world applications.
  • Where: The areas of application, ranging from business and economics, engineering and physics, health and medicine, computer science and AI, to mining engineering and metallurgy.
  • Who: The practitioners who apply Applied Calculus, such as scientists, engineers, economists, and data analysts.
  • How: The methods and tools used, both analytical techniques and modern computational software.

This structure helps learners understand the role of calculus as an applied, relevant, and essential discipline for addressing challenges across diverse fields.