A.3 Solutions (03)

ds4psy: Solutions 3

Here are the solutions of the exercises on essential dplyr commands of Chapter 3 (Section 3.5).

A.3.1 Exercise 1

Reshaping vs. reducing data

Discuss the main dplyr functions in terms of reshaping and reducing data (as introduced in Section 3.1.1).

Solution

Using the overview of essential dplyr functions (in Section 3.2), we can say:

arrange() reshapes data by sorting cases (rows);
filter() and slice() reduce data by selecting cases (rows) by logical conditions or number;
select() reduces data by selecting or reshapes data by reordering variables (columns);
mutate() reduces and enhances data by computing new variables (columns) and adding them to the existing ones;
summarise() reduces data by aggregating/collapsing multiple values of a variable (rows of a column) to a single one;
group_by() and ungroup() reshape data (in a subtle way by) changing the unit of aggregation (in combination with mutate() and summarise()). This is usually done as a preparatory step for reducing or enhancing data.

A.3.2 Exercise 2

Star and R wars

We start tackling the tidyverse by uncovering even more facts about the dplyr::starwars universe. Answer the following questions by using pipes of basic dplyr commands (i.e., by arranging, filtering, selecting, grouping, counting, summarizing).

Save the tibble dplyr::starwars as sw and report its dimensions.

## Load data: ----- 
sw <- dplyr::starwars
# ?dplyr::starwars  # codebook of variables

## Basic data properties: ---- 
# sw     # print tibble
dim(sw)  # 87 rows (denoting individuals) x 13 columns (variables) 
#> [1] 87 14

Known unknowns

How many missing (NA) values does sw contain?
Which variable (column) has the most missing values?
Which individuals come from an unknown (missing) homeworld but have a known birth_year or known mass?

Solution

## Missing data: ----- 

# How many missing data points?
sum(is.na(sw))  # => 101 missing values.
#> [1] 105

# Which individuals come from an unknown (missing) homeworld 
# but have a known birth_year or mass? 
sw %>% 
  filter(is.na(homeworld), !is.na(mass) | !is.na(birth_year))
#> # A tibble: 3 × 14
#>   name         height  mass hair_…¹ skin_…² eye_c…³ birth…⁴ sex   gender homew…⁵
#>   <chr>         <int> <dbl> <chr>   <chr>   <chr>     <dbl> <chr> <chr>  <chr>  
#> 1 Yoda             66    17 white   green   brown       896 male  mascu… <NA>   
#> 2 IG-88           200   140 none    metal   red          15 none  mascu… <NA>   
#> 3 Qui-Gon Jinn    193    89 brown   fair    blue         92 male  mascu… <NA>   
#> # … with 4 more variables: species <chr>, films <list>, vehicles <list>,
#> #   starships <list>, and abbreviated variable names ¹hair_color, ²skin_color,
#> #   ³eye_color, ⁴birth_year, ⁵homeworld

# Which variable (column) has the most missing values?
colSums(is.na(sw))  # => birth_year has 44 missing values
#>       name     height       mass hair_color skin_color  eye_color birth_year 
#>          0          6         28          5          0          0         44 
#>        sex     gender  homeworld    species      films   vehicles  starships 
#>          4          4         10          4          0          0          0
colMeans(is.na(sw)) #    (amounting to 50.1% of all cases). 
#>       name     height       mass hair_color skin_color  eye_color birth_year 
#> 0.00000000 0.06896552 0.32183908 0.05747126 0.00000000 0.00000000 0.50574713 
#>        sex     gender  homeworld    species      films   vehicles  starships 
#> 0.04597701 0.04597701 0.11494253 0.04597701 0.00000000 0.00000000 0.00000000

## (x) Replace all missing values of `hair_color` (in the variable `sw$hair_color`) by "bald": 
# sw$hair_color[is.na(sw$hair_color)] <- "bald"

Gender issues

How many humans are contained in sw overall and by gender?
How many and which individuals in sw are neither male nor female?
Of which species in sw exist at least 2 different gender values?

Solution

## (c) Gender issues: ----- 

# (+) How many humans are there of each gender?
sw %>% 
  filter(species == "Human") %>%
  group_by(gender) %>%
  count()
#> # A tibble: 2 × 2
#> # Groups:   gender [2]
#>   gender        n
#>   <chr>     <int>
#> 1 feminine      9
#> 2 masculine    26

## Answer: 35 Humans in total: 9 females, 26 male.

# (+) How many and which individuals are neither male nor female?
sw %>% 
  filter(gender != "male", gender != "female")
#> # A tibble: 83 × 14
#>    name        height  mass hair_…¹ skin_…² eye_c…³ birth…⁴ sex   gender homew…⁵
#>    <chr>        <int> <dbl> <chr>   <chr>   <chr>     <dbl> <chr> <chr>  <chr>  
#>  1 Luke Skywa…    172    77 blond   fair    blue       19   male  mascu… Tatooi…
#>  2 C-3PO          167    75 <NA>    gold    yellow    112   none  mascu… Tatooi…
#>  3 R2-D2           96    32 <NA>    white,… red        33   none  mascu… Naboo  
#>  4 Darth Vader    202   136 none    white   yellow     41.9 male  mascu… Tatooi…
#>  5 Leia Organa    150    49 brown   light   brown      19   fema… femin… Aldera…
#>  6 Owen Lars      178   120 brown,… light   blue       52   male  mascu… Tatooi…
#>  7 Beru White…    165    75 brown   light   blue       47   fema… femin… Tatooi…
#>  8 R5-D4           97    32 <NA>    white,… red        NA   none  mascu… Tatooi…
#>  9 Biggs Dark…    183    84 black   light   brown      24   male  mascu… Tatooi…
#> 10 Obi-Wan Ke…    182    77 auburn… fair    blue-g…    57   male  mascu… Stewjon
#> # … with 73 more rows, 4 more variables: species <chr>, films <list>,
#> #   vehicles <list>, starships <list>, and abbreviated variable names
#> #   ¹hair_color, ²skin_color, ³eye_color, ⁴birth_year, ⁵homeworld

# (+) Of which species are there at least 2 different gender values?
sw %>%
  group_by(species, gender) %>%
  count() %>%  # table shows species by gender: 
  group_by(species) %>%  # Which species appear more than once in this table? 
  count() %>%
  filter(n > 1)
#> # A tibble: 4 × 2
#> # Groups:   species [4]
#>   species      n
#>   <chr>    <int>
#> 1 Droid        2
#> 2 Human        2
#> 3 Kaminoan     2
#> 4 Twi'lek      2

# alternative (and shorter) solution:
sw %>%
  group_by(species) %>%
  summarise(n_gender_vals = n_distinct(gender)) %>%
  filter(n_gender_vals >= 2)
#> # A tibble: 4 × 2
#>   species  n_gender_vals
#>   <chr>            <int>
#> 1 Droid                2
#> 2 Human                2
#> 3 Kaminoan             2
#> 4 Twi'lek              2

Bonus task: R typically provides many ways to obtain a solution. Let’s gain an overview of the gender distribution in our sw dataset in three different ways:
- Use a dplyr pipe to compute a summary table tb that counts the frequency of each gender in sw.
- Use ggplot2 on the raw data of sw to create a bar chart (A) that shows the same gender distribution.
- Use ggplot2 on the summary table tb to create a bar chart (B) that shows the same gender distribution.

Solution

Computing the summary table tb is straightforward:

# Summary table:
tb <- sw %>%
  group_by(gender) %>%
  count()

tb
#> # A tibble: 3 × 2
#> # Groups:   gender [3]
#>   gender        n
#>   <chr>     <int>
#> 1 feminine     17
#> 2 masculine    66
#> 3 <NA>          4

Creating the same gender distribution as two plots:
- A: from the raw data sw
- B: from the summary table tb

# Define some colors:
my_cols <- unikn::usecol(c(Pinky, Seegruen, Seeblau, Grau))

# Plot A: From raw data
ggplot(sw, aes(x = gender)) +
  geom_bar(aes(fill = gender)) + 
  # Set labels, colors, and theme: 
  labs(title = "Gender distribution of the sw Universe", tag = "A",  
       x = "Gender", y = "Frequency", caption = "Using raw data sw.") + 
  scale_fill_manual(name = "Gender:", values = my_cols, na.value = "black") + 
  ds4psy::theme_ds4psy()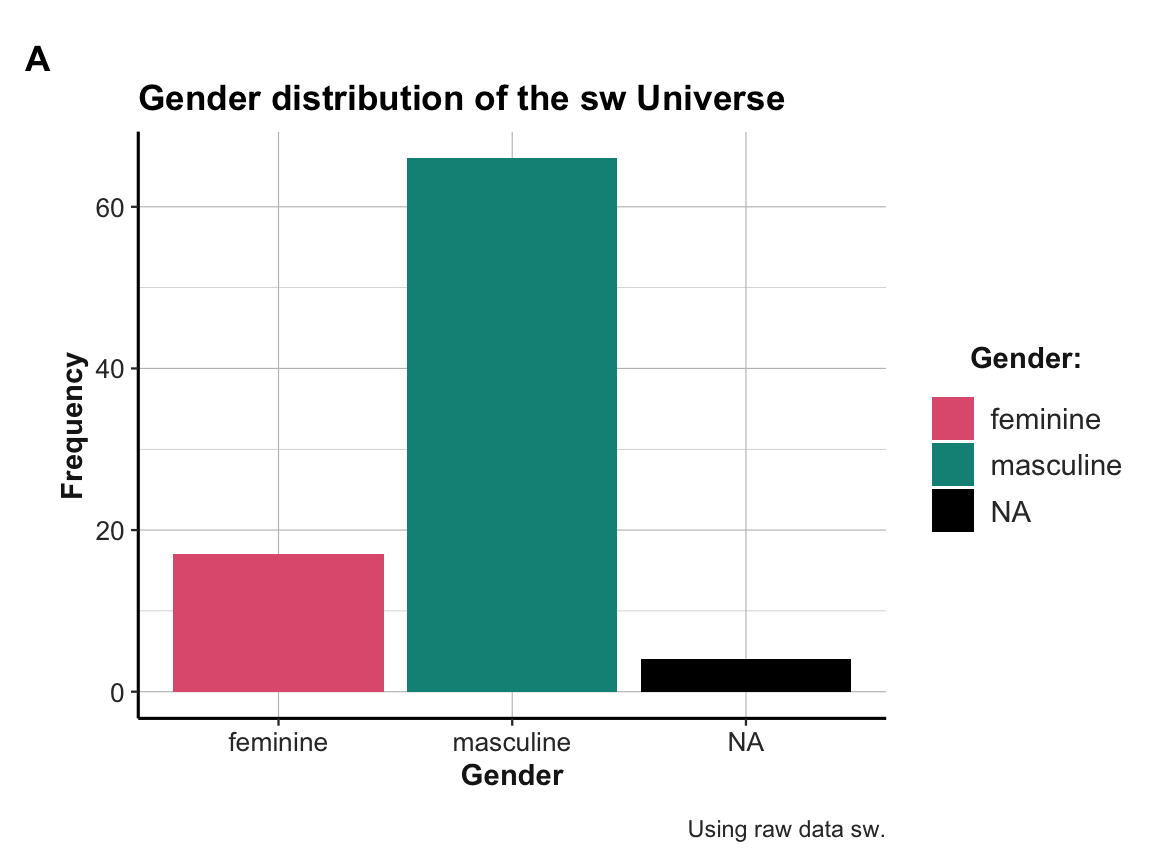


# Plot B: From summary table:
ggplot(tb, aes(x = gender, y = n)) +
  geom_bar(aes(fill = gender), stat = "identity") + 
  # Set labels, colors, and theme: 
  labs(title = "Gender distribution of the sw Universe", tag = "B", 
       x = "Gender", y = "Frequency", caption = "Using summary data tb.") + 
  scale_fill_manual(name = "Gender:", values = my_cols, na.value = "black") + 
  ds4psy::theme_ds4psy()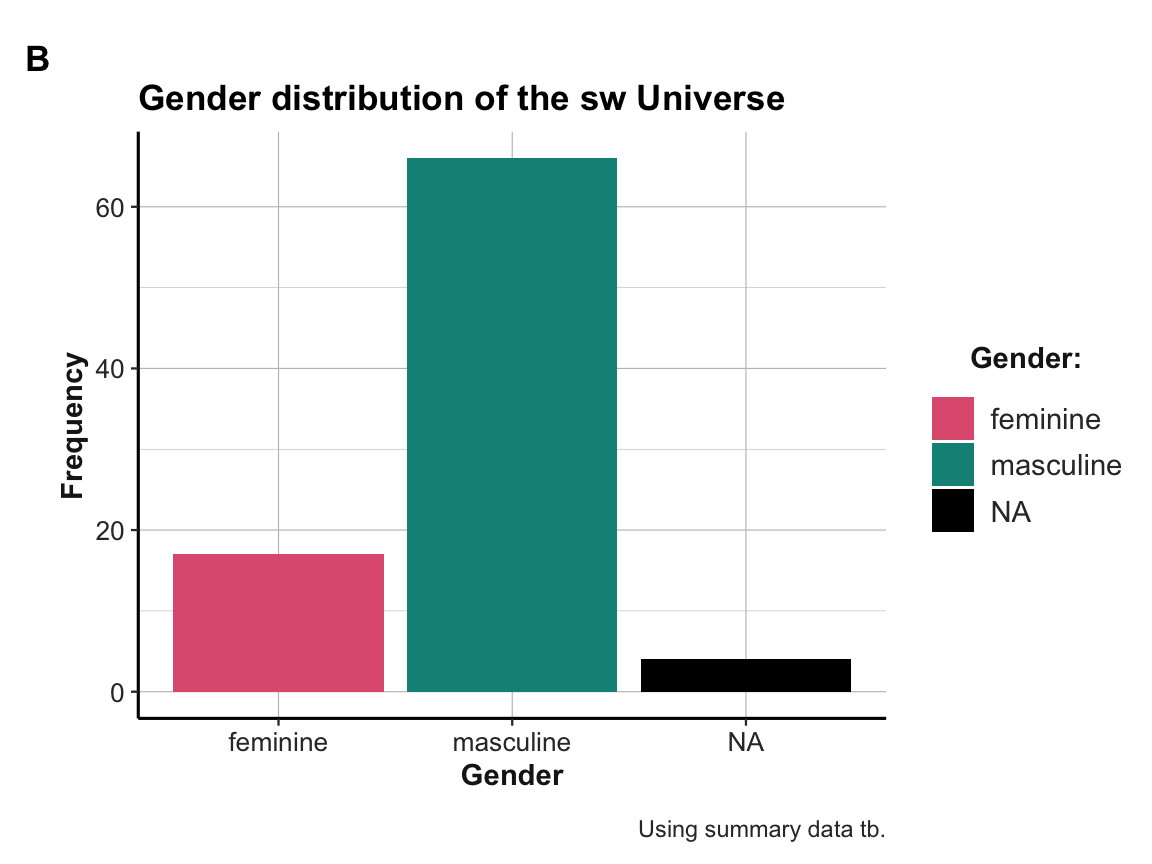

Note: Take a moment to reflect on the differences between both plots:

Both plots may look the same, but are internally quite different:

Plot A uses the raw data sw as its input and computes the frequency counts on the y-axis (as the default setting of geom_bar is stat = "count" and the resulting counts are automatically mapped to the y-axis).
Plot B uses the summary table tb as its input and maps the existing values of the column n on the y-axis. This requires setting the aesthetics to y = n and using stat = "identity" for geom_bar.)

Which of these ways we decide to use to plot summary results is a matter of preference, but has consequences:

On the one hand, using both a dplyr pipe and a ggplot2 command that re-computes the same counts (in Plot A) could help us to double-check our results. For instance, a common error is omitting the na.value argument when choosing your own colors with scale_fill_manual. This would drop the NA values from the plot — which we may never notice, if we had not computed the summary table tb before.
On the other hand, if we already have a summary table tb, creating Plot B ensures that we are plotting exactly the contents of this table. Anything that changes the table will also change the plot.

Popular homes and heights

From which homeworld do the most indidividuals (rows) come from?
What is the mean height of all individuals with orange eyes from the most popular homeworld?

Solution

## (d) Homeworld issues: ----- 

# (+) Popular homes: From which homeworld do the most indidividuals (rows) come from? 
sw %>%
  group_by(homeworld) %>%
  count() %>%
  arrange(desc(n))
#> # A tibble: 49 × 2
#> # Groups:   homeworld [49]
#>    homeworld     n
#>    <chr>     <int>
#>  1 Naboo        11
#>  2 Tatooine     10
#>  3 <NA>         10
#>  4 Alderaan      3
#>  5 Coruscant     3
#>  6 Kamino        3
#>  7 Corellia      2
#>  8 Kashyyyk      2
#>  9 Mirial        2
#> 10 Ryloth        2
#> # … with 39 more rows
# => Naboo (with 11 individuals)

# (+) What is the mean height of all individuals with orange eyes from the most popular homeworld? 
sw %>% 
  filter(homeworld == "Naboo", eye_color == "orange") %>%
  summarise(n = n(),
            mn_height = mean(height))
#> # A tibble: 1 × 2
#>       n mn_height
#>   <int>     <dbl>
#> 1     3      209.

## Note: 
sw %>% 
  filter(eye_color == "orange") # => 8 individuals
#> # A tibble: 8 × 14
#>   name         height  mass hair_…¹ skin_…² eye_c…³ birth…⁴ sex   gender homew…⁵
#>   <chr>         <int> <dbl> <chr>   <chr>   <chr>     <dbl> <chr> <chr>  <chr>  
#> 1 Jabba Desil…    175  1358 <NA>    green-… orange      600 herm… mascu… Nal Hu…
#> 2 Ackbar          180    83 none    brown … orange       41 male  mascu… Mon Ca…
#> 3 Jar Jar Bin…    196    66 none    orange  orange       52 male  mascu… Naboo  
#> 4 Roos Tarpals    224    82 none    grey    orange       NA male  mascu… Naboo  
#> 5 Rugor Nass      206    NA none    green   orange       NA male  mascu… Naboo  
#> 6 Sebulba         112    40 none    grey, … orange       NA male  mascu… Malast…
#> 7 Ben Quadina…    163    65 none    grey, … orange       NA male  mascu… Tund   
#> 8 Saesee Tiin     188    NA none    pale    orange       NA male  mascu… Iktotch
#> # … with 4 more variables: species <chr>, films <list>, vehicles <list>,
#> #   starships <list>, and abbreviated variable names ¹hair_color, ²skin_color,
#> #   ³eye_color, ⁴birth_year, ⁵homeworld

# (+) What is the mass and homeworld of the smallest droid?
sw %>% 
  filter(species == "Droid") %>%
  arrange(height)
#> # A tibble: 6 × 14
#>   name   height  mass hair_color skin_color eye_c…¹ birth…² sex   gender homew…³
#>   <chr>   <int> <dbl> <chr>      <chr>      <chr>     <dbl> <chr> <chr>  <chr>  
#> 1 R2-D2      96    32 <NA>       white, bl… red          33 none  mascu… Naboo  
#> 2 R4-P17     96    NA none       silver, r… red, b…      NA none  femin… <NA>   
#> 3 R5-D4      97    32 <NA>       white, red red          NA none  mascu… Tatooi…
#> 4 C-3PO     167    75 <NA>       gold       yellow      112 none  mascu… Tatooi…
#> 5 IG-88     200   140 none       metal      red          15 none  mascu… <NA>   
#> 6 BB8        NA    NA none       none       black        NA none  mascu… <NA>   
#> # … with 4 more variables: species <chr>, films <list>, vehicles <list>,
#> #   starships <list>, and abbreviated variable names ¹eye_color, ²birth_year,
#> #   ³homeworld

Size and mass issues

Compute the median, mean, and standard deviation of height for all droids.
Compute the average height and mass by species and save the result as h_m.
Sort h_m to list the three species with the smallest individuals (in terms of mean height).
Sort h_m to list the three species with the heaviest individuals (in terms of median mass).

Solution

## Size and mass issues (group summaries): ----- 

# (+) Compute the median, mean, and standard deviation of `height` for all droids.
sw %>%
  filter(species == "Droid") %>%
  summarise(n = n(),
            not_NA_h = sum(!is.na(height)),
            md_height = median(height, na.rm = TRUE),
            mn_height = mean(height, na.rm = TRUE),
            sd_height = sd(height, na.rm = TRUE))
#> # A tibble: 1 × 5
#>       n not_NA_h md_height mn_height sd_height
#>   <int>    <int>     <int>     <dbl>     <dbl>
#> 1     6        5        97      131.      49.1

# (+) Compute the average height and mass by species and save the result as `h_m`:
h_m <- sw %>%
  group_by(species) %>%
  summarise(n = n(),
            not_NA_h = sum(!is.na(height)),
            mn_height = mean(height, na.rm = TRUE),
            not_NA_m = sum(!is.na(mass)),
            md_mass = median(mass, na.rm = TRUE)
            )
h_m
#> # A tibble: 38 × 6
#>    species       n not_NA_h mn_height not_NA_m md_mass
#>    <chr>     <int>    <int>     <dbl>    <int>   <dbl>
#>  1 Aleena        1        1       79         1    15  
#>  2 Besalisk      1        1      198         1   102  
#>  3 Cerean        1        1      198         1    82  
#>  4 Chagrian      1        1      196         0    NA  
#>  5 Clawdite      1        1      168         1    55  
#>  6 Droid         6        5      131.        4    53.5
#>  7 Dug           1        1      112         1    40  
#>  8 Ewok          1        1       88         1    20  
#>  9 Geonosian     1        1      183         1    80  
#> 10 Gungan        3        3      209.        2    74  
#> # … with 28 more rows

# (+) Use `h_m` to list the 3 species with the smallest individuals (in terms of mean height)?
h_m %>% arrange(mn_height) %>% slice(1:3)
#> # A tibble: 3 × 6
#>   species            n not_NA_h mn_height not_NA_m md_mass
#>   <chr>          <int>    <int>     <dbl>    <int>   <dbl>
#> 1 Yoda's species     1        1        66        1      17
#> 2 Aleena             1        1        79        1      15
#> 3 Ewok               1        1        88        1      20

# (+) Use `h_m` to list the 3 species with the heaviest individuals (in terms of median mass)?
h_m %>% arrange(desc(md_mass)) %>%  slice(1:3)
#> # A tibble: 3 × 6
#>   species     n not_NA_h mn_height not_NA_m md_mass
#>   <chr>   <int>    <int>     <dbl>    <int>   <dbl>
#> 1 Hutt        1        1       175        1    1358
#> 2 Kaleesh     1        1       216        1     159
#> 3 Wookiee     2        2       231        2     124

Bonus tasks

The following bonus tasks are more difficult, but can be solved with a single dplyr pipe:

How many individuals come from the three most frequent (known) species?
Which individuals are more than 20% lighter (in terms of mass) than the average mass of individuals of their own homeworld?

Solution

# How many individuals come from the 3 most frequent (known) species?
sw %>%
  group_by(species) %>%
  count %>%
  arrange(desc(n)) %>%
  filter(n > 1)
#> # A tibble: 9 × 2
#> # Groups:   species [9]
#>   species      n
#>   <chr>    <int>
#> 1 Human       35
#> 2 Droid        6
#> 3 <NA>         4
#> 4 Gungan       3
#> 5 Kaminoan     2
#> 6 Mirialan     2
#> 7 Twi'lek      2
#> 8 Wookiee      2
#> 9 Zabrak       2

# Which individuals are more than 20% lighter (in terms of mass) 
# than the average mass of individuals of their own homeworld?
sw %>%
  select(name, homeworld, mass) %>%
  group_by(homeworld) %>%
  mutate(n_notNA_mass = sum(!is.na(mass)),  
         mn_mass = mean(mass, na.rm = TRUE),
         lighter = mass < (mn_mass - (.20 * mn_mass))
         ) %>%
  filter(lighter == TRUE)
#> # A tibble: 5 × 6
#> # Groups:   homeworld [4]
#>   name          homeworld  mass n_notNA_mass mn_mass lighter
#>   <chr>         <chr>     <dbl>        <int>   <dbl> <lgl>  
#> 1 R2-D2         Naboo        32            6    64.2 TRUE   
#> 2 Leia Organa   Alderaan     49            2    64   TRUE   
#> 3 R5-D4         Tatooine     32            8    85.4 TRUE   
#> 4 Yoda          <NA>         17            3    82   TRUE   
#> 5 Padmé Amidala Naboo        45            6    64.2 TRUE

A.3.3 Exercise 3

Sleeping mammals

The dataset ggplot2::msleep contains a mammals sleep dataset (see ?msleep for details and the definition of variables).

Save the data as sp and check the dimensions, variable types, and number of missing values in the dataset.

Solution

## Data: 
# ?msleep  # check variables     
sp <- ggplot2::msleep

# Check: 
dim(sp)        # 83 x 11 variables
#> [1] 83 11
glimpse(sp)    # 5 <chr> and 6 <dbl>
#> Rows: 83
#> Columns: 11
#> $ name         <chr> "Cheetah", "Owl monkey", "Mountain beaver", "Greater shor…
#> $ genus        <chr> "Acinonyx", "Aotus", "Aplodontia", "Blarina", "Bos", "Bra…
#> $ vore         <chr> "carni", "omni", "herbi", "omni", "herbi", "herbi", "carn…
#> $ order        <chr> "Carnivora", "Primates", "Rodentia", "Soricomorpha", "Art…
#> $ conservation <chr> "lc", NA, "nt", "lc", "domesticated", NA, "vu", NA, "dome…
#> $ sleep_total  <dbl> 12.1, 17.0, 14.4, 14.9, 4.0, 14.4, 8.7, 7.0, 10.1, 3.0, 5…
#> $ sleep_rem    <dbl> NA, 1.8, 2.4, 2.3, 0.7, 2.2, 1.4, NA, 2.9, NA, 0.6, 0.8, …
#> $ sleep_cycle  <dbl> NA, NA, NA, 0.1333333, 0.6666667, 0.7666667, 0.3833333, N…
#> $ awake        <dbl> 11.9, 7.0, 9.6, 9.1, 20.0, 9.6, 15.3, 17.0, 13.9, 21.0, 1…
#> $ brainwt      <dbl> NA, 0.01550, NA, 0.00029, 0.42300, NA, NA, NA, 0.07000, 0…
#> $ bodywt       <dbl> 50.000, 0.480, 1.350, 0.019, 600.000, 3.850, 20.490, 0.04…
sum(is.na(sp)) # 136 missing values
#> [1] 136

Arranging and filtering data

Use the dplyr-verbs arrange(), group_by(), and filter() to answer the following questions by creating ordered subsets of the data:

Arrange the rows (alphabetically) by vore, order, and name, and report the genus of the top three mammals.
What is the most common type of vore in the data? How many omnivores are there?
What is the most common order in the dataset? Are there more exemplars of the order “Carnivora” or “Primates”?
Which two mammals of the order “Primates” have the longest and shortest sleep_total times?

Solution

# Arranging rows:
sp1 <- sp %>%
  arrange(vore, order, name)
sp1$genus[1:3]  # => top 3: "Vulpes"   "Phoca"    "Acinonyx"
#> [1] "Vulpes"   "Phoca"    "Acinonyx"

# Counting common vores:
# (a) short solution:
sp %>%
  count(vore) %>%
  arrange(desc(n))  
#> # A tibble: 5 × 2
#>   vore        n
#>   <chr>   <int>
#> 1 herbi      32
#> 2 omni       20
#> 3 carni      19
#> 4 <NA>        7
#> 5 insecti     5

# (a) is the same as (b): 
sp %>% 
  group_by(vore) %>%
  tally() %>%
  arrange(desc(n))
#> # A tibble: 5 × 2
#>   vore        n
#>   <chr>   <int>
#> 1 herbi      32
#> 2 omni       20
#> 3 carni      19
#> 4 <NA>        7
#> 5 insecti     5

# (b) is the same as (c):  
sp %>% 
  group_by(vore) %>%
  summarise(n = n()) %>%
  arrange(desc(n))
#> # A tibble: 5 × 2
#>   vore        n
#>   <chr>   <int>
#> 1 herbi      32
#> 2 omni       20
#> 3 carni      19
#> 4 <NA>        7
#> 5 insecti     5

# => 32 herbivores, 20 omnivores

# Counting common orders: 
sp %>% 
  count(order) %>%
  arrange(desc(n)) 
#> # A tibble: 19 × 2
#>    order               n
#>    <chr>           <int>
#>  1 Rodentia           22
#>  2 Carnivora          12
#>  3 Primates           12
#>  4 Artiodactyla        6
#>  5 Soricomorpha        5
#>  6 Cetacea             3
#>  7 Hyracoidea          3
#>  8 Perissodactyla      3
#>  9 Chiroptera          2
#> 10 Cingulata           2
#> 11 Didelphimorphia     2
#> 12 Diprotodontia       2
#> 13 Erinaceomorpha      2
#> 14 Proboscidea         2
#> 15 Afrosoricida        1
#> 16 Lagomorpha          1
#> 17 Monotremata         1
#> 18 Pilosa              1
#> 19 Scandentia          1

# OR: 
sp %>% 
  group_by(order) %>%
  count() %>%
  arrange(desc(n)) 
#> # A tibble: 19 × 2
#> # Groups:   order [19]
#>    order               n
#>    <chr>           <int>
#>  1 Rodentia           22
#>  2 Carnivora          12
#>  3 Primates           12
#>  4 Artiodactyla        6
#>  5 Soricomorpha        5
#>  6 Cetacea             3
#>  7 Hyracoidea          3
#>  8 Perissodactyla      3
#>  9 Chiroptera          2
#> 10 Cingulata           2
#> 11 Didelphimorphia     2
#> 12 Diprotodontia       2
#> 13 Erinaceomorpha      2
#> 14 Proboscidea         2
#> 15 Afrosoricida        1
#> 16 Lagomorpha          1
#> 17 Monotremata         1
#> 18 Pilosa              1
#> 19 Scandentia          1
# => 22 Rodentia, 12 Carnivora = 12 Primates

# Primates with longest and shortest sleep_total times:
sp %>% 
  filter(order == "Primates") %>%
  arrange(desc(sleep_total)) 
#> # A tibble: 12 × 11
#>    name   genus vore  order conse…¹ sleep…² sleep…³ sleep…⁴ awake brainwt bodywt
#>    <chr>  <chr> <chr> <chr> <chr>     <dbl>   <dbl>   <dbl> <dbl>   <dbl>  <dbl>
#>  1 Owl m… Aotus omni  Prim… <NA>       17       1.8  NA       7    0.0155  0.48 
#>  2 Slow … Nyct… carni Prim… <NA>       11      NA    NA      13    0.0125  1.4  
#>  3 Potto  Pero… omni  Prim… lc         11      NA    NA      13   NA       1.1  
#>  4 Patas… Eryt… omni  Prim… lc         10.9     1.1  NA      13.1  0.115  10    
#>  5 Macaq… Maca… omni  Prim… <NA>       10.1     1.2   0.75   13.9  0.179   6.8  
#>  6 Grivet Cerc… omni  Prim… lc         10       0.7  NA      14   NA       4.75 
#>  7 Galago Gala… omni  Prim… <NA>        9.8     1.1   0.55   14.2  0.005   0.2  
#>  8 Chimp… Pan   omni  Prim… <NA>        9.7     1.4   1.42   14.3  0.44   52.2  
#>  9 Squir… Saim… omni  Prim… <NA>        9.6     1.4  NA      14.4  0.02    0.743
#> 10 Mongo… Lemur herbi Prim… vu          9.5     0.9  NA      14.5 NA       1.67 
#> 11 Baboon Papio omni  Prim… <NA>        9.4     1     0.667  14.6  0.18   25.2  
#> 12 Human  Homo  omni  Prim… <NA>        8       1.9   1.5    16    1.32   62    
#> # … with abbreviated variable names ¹conservation, ²sleep_total, ³sleep_rem,
#> #   ⁴sleep_cycle
# => max: Owl monkey: 17 hours, min: Human 8 hours.

Computing new variables

Solve the following tasks by combining the dplyr commands mutate, group_by, and summarise:

Compute a variable sleep_awake_sum that adds the sleep_total time and the awake time of each mammal. What result do you expect and get?
Which animals have the smallest and largest brain to body ratio (in terms of weight)? How many mammals have a larger ratio than humans?
What is the minimum, average (mean), and maximum sleep cycle length for each vore? (Hint: First group the data by group_by, then use summarise on the sleep_cycle variable, but also count the number of NA values for each vore. When computing grouped summaries, NA values can be removed by na.rm = TRUE.)
Replace your summarise verb in the previous task by mutate. What do you get as a result? (Hint: The last two tasks illustrate the difference between mutate and grouped mutate commands.)

Solution

# Computing `sleep_awake_sum`: 
sp2 <- sp %>%
  mutate(sleep_awake_sum = sleep_total + awake)
sp2$sleep_awake_sum  # => all 24 hours 
#>  [1] 24.00 24.00 24.00 24.00 24.00 24.00 24.00 24.00 24.00 24.00 24.00 24.00
#> [13] 24.00 24.00 24.00 24.00 24.00 24.00 24.00 24.00 24.00 24.00 24.00 24.00
#> [25] 24.00 24.00 24.00 24.00 24.00 24.00 24.05 24.00 24.00 24.00 24.00 24.00
#> [37] 24.00 24.00 24.00 24.00 24.00 24.00 24.00 24.00 24.00 24.00 24.00 24.00
#> [49] 24.00 24.00 24.00 24.00 24.00 24.00 24.00 24.00 24.00 24.00 24.00 24.05
#> [61] 24.00 24.00 24.00 24.00 24.00 24.00 24.00 24.00 24.00 24.00 24.00 24.00
#> [73] 24.00 24.00 24.00
#>  [ reached getOption("max.print") -- omitted 8 entries ]

# Computing brain to body ratios:
sp3 <- sp %>%
  mutate(brain_to_body_wt = brainwt / bodywt) %>%
  arrange(brain_to_body_wt)

sp3$name[1] # => smallest ratio: Cow
#> [1] "Cow"

sp3 %>% 
  arrange(desc(brain_to_body_wt))
#> # A tibble: 83 × 12
#>    name   genus vore  order conse…¹ sleep…² sleep…³ sleep…⁴ awake brainwt bodywt
#>    <chr>  <chr> <chr> <chr> <chr>     <dbl>   <dbl>   <dbl> <dbl>   <dbl>  <dbl>
#>  1 Thirt… Sper… herbi Rode… lc         13.8     3.4   0.217  10.2 0.004    0.101
#>  2 Owl m… Aotus omni  Prim… <NA>       17       1.8  NA       7   0.0155   0.48 
#>  3 Lesse… Cryp… omni  Sori… lc          9.1     1.4   0.15   14.9 0.00014  0.005
#>  4 Squir… Saim… omni  Prim… <NA>        9.6     1.4  NA      14.4 0.02     0.743
#>  5 Macaq… Maca… omni  Prim… <NA>       10.1     1.2   0.75   13.9 0.179    6.8  
#>  6 Littl… Myot… inse… Chir… <NA>       19.9     2     0.2     4.1 0.00025  0.01 
#>  7 Galago Gala… omni  Prim… <NA>        9.8     1.1   0.55   14.2 0.005    0.2  
#>  8 Mole … Spal… <NA>  Rode… <NA>       10.6     2.4  NA      13.4 0.003    0.122
#>  9 Tree … Tupa… omni  Scan… <NA>        8.9     2.6   0.233  15.1 0.0025   0.104
#> 10 Human  Homo  omni  Prim… <NA>        8       1.9   1.5    16   1.32    62    
#> # … with 73 more rows, 1 more variable: brain_to_body_wt <dbl>, and abbreviated
#> #   variable names ¹conservation, ²sleep_total, ³sleep_rem, ⁴sleep_cycle
# => largest ratio: Thirteen-lined ground squirrel, 
#    9 mammals have larger brain_to_body_wt than Human.

# Computing sleep cycle length for each `vore`: 
sp %>%
  group_by(vore) %>%
  summarise(n = n(),
            n_NA = sum(is.na(sleep_cycle)), 
            non_NA = sum(!is.na(sleep_cycle)),
            min_cyc = min(sleep_cycle, na.rm = TRUE),
            mn_cyc = mean(sleep_cycle, na.rm = TRUE),
            max_cyc = max(sleep_cycle, na.rm = TRUE)
            )
#> # A tibble: 5 × 7
#>   vore        n  n_NA non_NA min_cyc mn_cyc max_cyc
#>   <chr>   <int> <int>  <int>   <dbl>  <dbl>   <dbl>
#> 1 carni      19    14      5   0.333  0.373   0.417
#> 2 herbi      32    20     12   0.117  0.418   1    
#> 3 insecti     5     2      3   0.117  0.161   0.2  
#> 4 omni       20     9     11   0.133  0.592   1.5  
#> 5 <NA>        7     6      1   0.183  0.183   0.183

# Replacing summarise by mutate: 
sp4 <- sp %>%
  group_by(vore) %>%
  mutate(n = n(),
         n_NA = sum(is.na(sleep_cycle)), 
         non_NA = sum(!is.na(sleep_cycle)),
         min_cyc = min(sleep_cycle, na.rm = TRUE),
         mn_cyc = mean(sleep_cycle, na.rm = TRUE),
         max_cyc = max(sleep_cycle, na.rm = TRUE)
  )

# => A tibble that contains grouped summaries as 6 new variables: 
sp4 %>% 
  select(vore, name, sleep_cycle, n:max_cyc) %>%
  arrange(vore)
#> # A tibble: 83 × 9
#> # Groups:   vore [5]
#>    vore  name                  sleep…¹     n  n_NA non_NA min_cyc mn_cyc max_cyc
#>    <chr> <chr>                   <dbl> <int> <int>  <int>   <dbl>  <dbl>   <dbl>
#>  1 carni Cheetah                NA        19    14      5   0.333  0.373   0.417
#>  2 carni Northern fur seal       0.383    19    14      5   0.333  0.373   0.417
#>  3 carni Dog                     0.333    19    14      5   0.333  0.373   0.417
#>  4 carni Long-nosed armadillo    0.383    19    14      5   0.333  0.373   0.417
#>  5 carni Domestic cat            0.417    19    14      5   0.333  0.373   0.417
#>  6 carni Pilot whale            NA        19    14      5   0.333  0.373   0.417
#>  7 carni Gray seal              NA        19    14      5   0.333  0.373   0.417
#>  8 carni Thick-tailed opposum   NA        19    14      5   0.333  0.373   0.417
#>  9 carni Slow loris             NA        19    14      5   0.333  0.373   0.417
#> 10 carni Northern grasshopper…  NA        19    14      5   0.333  0.373   0.417
#> # … with 73 more rows, and abbreviated variable name ¹sleep_cycle

A.3.4 Exercise 4

Outliers

This exercise examines different possibilities for defining outliers and uses the outliers dataset of the ds4psy package (also available as out.csv at http://rpository.com/ds4psy/data/out.csv) to illustate and compare them. With respect to your insights into dplyr, this exercise helps disentangling mutate from grouped mutate commands.

Data on `outliers`

Use the outliers data (from the ds4psy package) or use the following read_csv() command to load the data into an R object entitled outliers:

# Data: 
outliers <- ds4psy::outliers  # from ds4psy package

## Alternatively, load csv data from online source (as comma-separated file): 
# outliers_2 <- readr::read_csv("http://rpository.com/ds4psy/data/out.csv")  # from online source

## Verify equality: 
# all.equal(ds4psy::outliers, outliers_2)

## Alternatively from a local data file: 
# outliers <- read_csv("out.csv")  # from current directory

Not all outliers are alike

An outlier can be defined as an individual whose value in some variable deviates by more than a given criterion (e.g., two standard deviations) from the mean of the variable. However, this definition is incomplete unless it also specifies the reference group over which the means and deviations are computed. In the following, we explore the implications of different reference groups.

Basic tasks

Save the data into a tibble outliers and report its number of observations and variables, and their types.
How many missing data values are there in outliers?
What is the gender (or sex) distribution in this sample?
Create a plot that shows the distribution of height values for each gender.

Solution

# Load and inspect data:
# outliers <- read_csv("out.csv") # read in csv-file
# outliers <- as_tibble(data)   # if data is not already a tibble
dim(outliers)  # => 1000 observations (rows) x 3 variables (columns)
#> [1] 1000    3

# Missing data points: 
sum(is.na(outliers))  # => 18 missing values
#> [1] 18

# Gender distribution: 
outliers %>% 
  group_by(sex) %>% 
  count()
#> # A tibble: 2 × 2
#> # Groups:   sex [2]
#>   sex        n
#>   <chr>  <int>
#> 1 female   507
#> 2 male     493
# => 50.7% females, 49.3% males.

# Distributions of `height` as density plot: 
ggplot(outliers, aes(x = height)) +
  geom_density(fill = "gold", alpha = 2/3) +
  geom_density(aes(fill = sex), alpha = 1/3) +
  labs(title = "Distribution of heights overall and by gender", 
       fill = "Gender") + 
  # scale_fill_brewer(palette = "Set1") +  # using Brewer palette
  scale_fill_manual(name = "Gender:", values = unikn::usecol(c(Pinky, Seeblau))) +  # unikn colors
  theme_bw()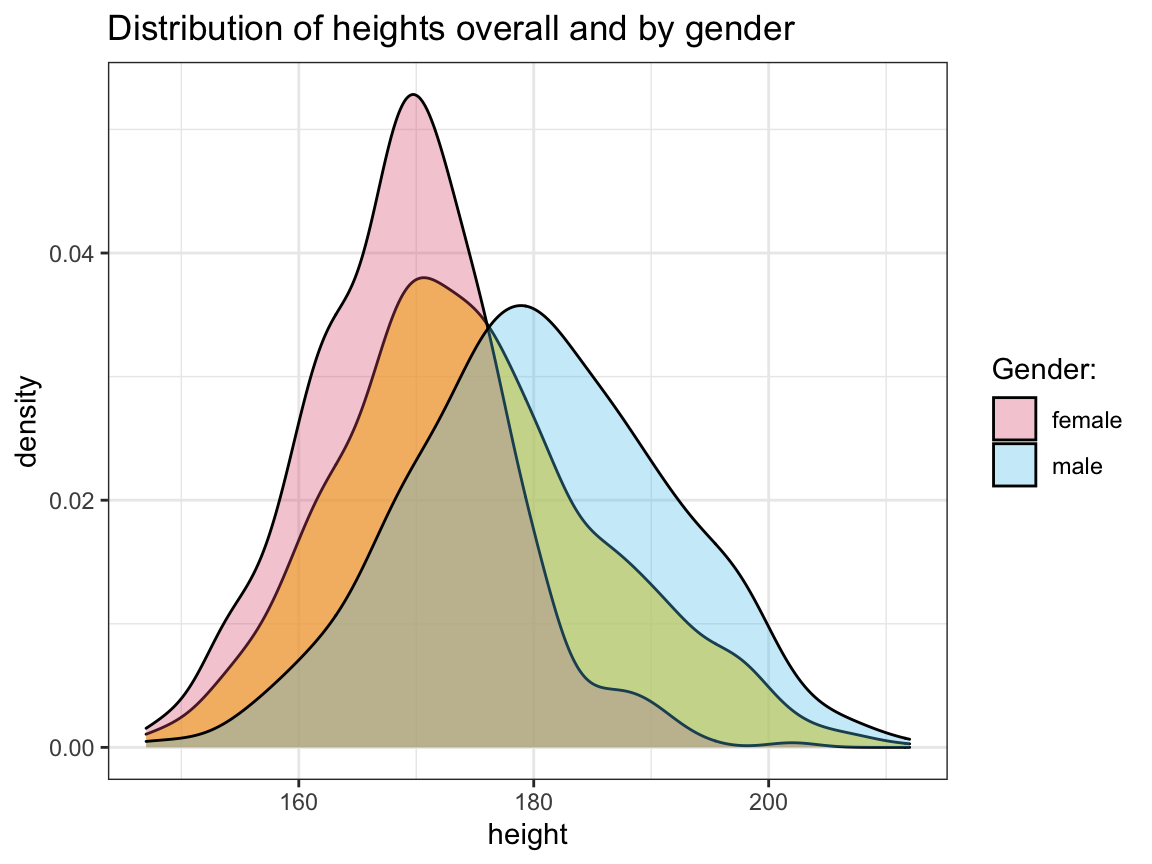


# Note: To avoid the warning about removing 18 cases with NA-values, 
#       we could first filter out those cases:
# non_NA_data <- filter(outliers, !is.na(height))

# Alternative solution as 2 histograms: 
ggplot(outliers) +
  facet_wrap(~sex) + 
  geom_histogram(aes(x = height, fill = sex), binwidth = 5, color = "grey10") +
  labs(title = "Distribution of heights by gender",
       x = "Height", y = "Frequency") +
  # scale_fill_brewer(name = "Gender:", palette = "Set1") +  # using Brewer palette
  scale_fill_manual(name = "Gender:", values = unikn::usecol(c(Pinky, Seeblau))) +  # unikn colors
  theme_bw()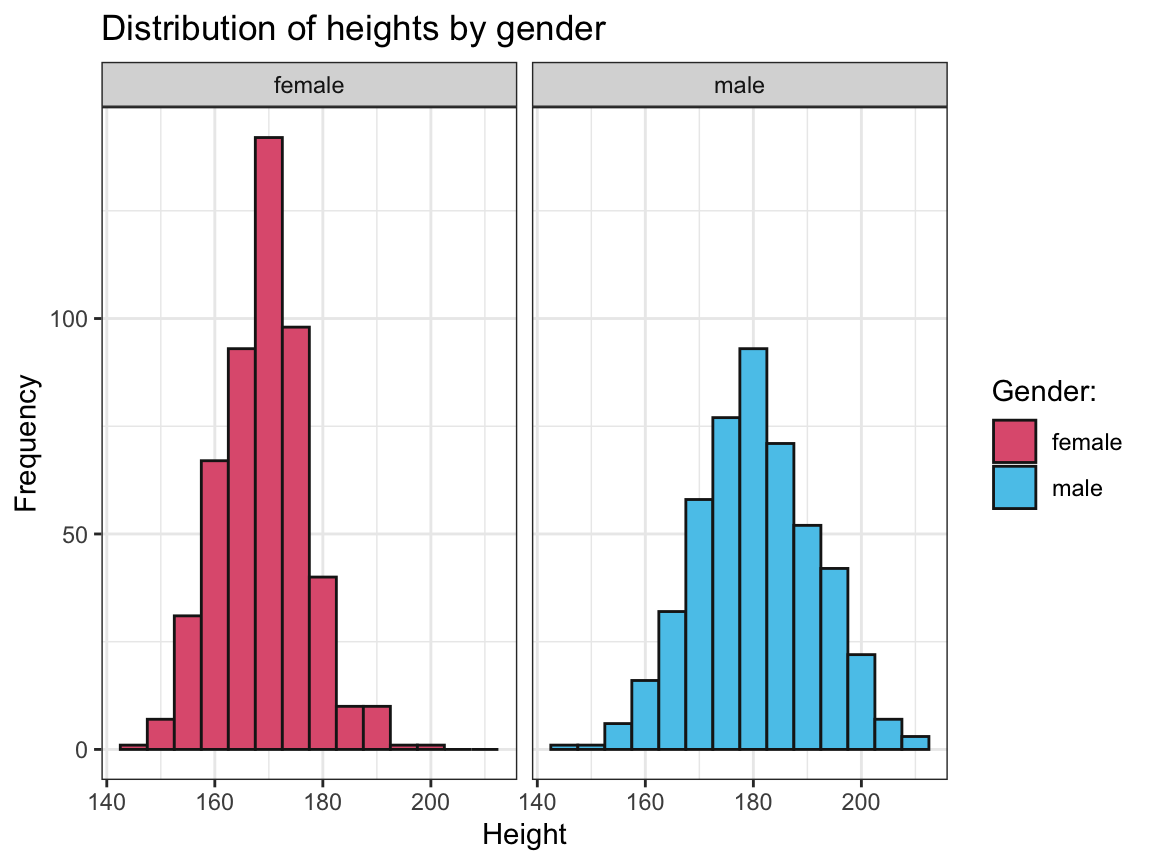

Defining different outliers

Compute 2 new variables that signal and distinguish between 2 types of outliers in terms of height:

outliers relative to the height of the overall sample (i.e., individuals with height values deviating more than 2 SD from the overall mean of height);
outliers relative to the height of some subgroup’s mean and SD. Here, a suitable subgroup to consider is every person’s gender (i.e., individuals with height values deviating more than 2 SD from the mean height of their own gender).

Hints: As both variable signal whether or not someone is an outlier they should be defined as logicals (being either TRUE or FALSE) and added as new columns to data (via appropriate mutate commands). While the 1st variable can be computed based on the mean and SD of the overall sample, the 2nd variable can be computed after grouping outliers by gender and then computing and using the corresponding mean and SD values. The absolute difference between 2 numeric values x and y is provided by abs(x - y).

Relative outliers

Now use the 2 new outlier variables to define (or filter) 2 subsets of the data that contain 2 subgroups of people:

out_1: Individuals (females and males) with height values that are outliers relative to both the entire sample and the sample of their own gender. How many such individuals are in outliers?
out_2: Individuals (females and males) with height values that are not outliers relative to the entire population, but are outliers relative to their own gender. How many such individuals are in outliers?

Solution

## Defining different outliers: ----- 

# Included in data_out (below), but also possible to do separately:  
# Compute the number, means and SD of height values in 2 ways: 

# 1. overall: 
outliers %>%
  summarise(n = n(),
            n_not_NA = sum(!is.na(height)),
            mn_height = mean(height, na.rm = TRUE),
            sd_height = sd(height, na.rm = TRUE))
#> # A tibble: 1 × 4
#>       n n_not_NA mn_height sd_height
#>   <int>    <int>     <dbl>     <dbl>
#> 1  1000      982      175.      11.3

# 2. by gender:
outliers %>%
  group_by(sex) %>%
  summarise(n = n(),
            n_not_NA = sum(!is.na(height)),
            mn_height = mean(height, na.rm = TRUE),
            sd_height = sd(height, na.rm = TRUE))
#> # A tibble: 2 × 5
#>   sex        n n_not_NA mn_height sd_height
#>   <chr>  <int>    <int>     <dbl>     <dbl>
#> 1 female   507      501      169.      8.19
#> 2 male     493      481      181.     11.0


# Detecting and marking outliers (by logical variables): 
# Compute the means, SDs, and corresponding outliers in 2 ways:
crit <- 2  # criterion value for detecting outliers (in SD units)

data_out <- outliers %>%      
  # 1. Compute means, SD, and outliers for overall sample: 
  mutate(mn_height  = mean(height, na.rm = TRUE),  
         sd_height  = sd(height, na.rm = TRUE),
         out_height = abs(height - mn_height) > (crit * sd_height)) %>%
  group_by(sex) %>%       
  # 2. Compute same metrics for subgroups (by sex):
  mutate(mn_sex_height  = mean(height, na.rm = TRUE), 
         sd_sex_height  = sd(height, na.rm = TRUE),
         out_sex_height = abs(height - mn_sex_height) > (crit * sd_sex_height))

knitr::kable(head(data_out))

id	sex	height	mn_height	sd_height	out_height	mn_sex_height	sd_sex_height	out_sex_height
nr.1	female	164	174.7006	11.26015	FALSE	169.0679	8.193619	FALSE
nr.2	male	178	174.7006	11.26015	FALSE	180.5676	11.026677	FALSE
nr.3	female	177	174.7006	11.26015	FALSE	169.0679	8.193619	FALSE
nr.4	male	188	174.7006	11.26015	FALSE	180.5676	11.026677	FALSE
nr.5	male	193	174.7006	11.26015	FALSE	180.5676	11.026677	FALSE
nr.6	female	168	174.7006	11.26015	FALSE	169.0679	8.193619	FALSE


## Relative outliers: ----- 

# Filter specific combinations of outliers:

# 1. Outliers relative to the entire population AND to their own gender: 
out_1 <- data_out %>%
  filter(out_height & out_sex_height) %>%
  arrange(sex, height)

nrow(out_1) # => 21 individuals. 
#> [1] 21

# 2. Outliers relative to their own gender, but NOT relative to the entire population:
out_2 <- data_out %>%
  filter(!out_height & out_sex_height) %>%
  arrange(sex, height)  

nrow(out_2) # => 24 individuals.
#> [1] 24

Bonus plots

Visualize the raw values and distributions of height for both types of outliers (out_1 and out_2) in 2 separate plots.
Interpret both plots by describing the height and sex combination of the individuals shown in each plot.

Solution

# Visualization and interpretation of both types of outliers: 

# 1. Showing out_1: 
ggplot(out_1, aes(x = sex, y = height)) +
  geom_violin(aes(fill = sex)) + 
  geom_jitter(size = 4, alpha = 2/3) + 
  # scale_fill_manual(values = c("firebrick", "steelblue3")) +
  scale_fill_manual(name = "Gender:", values = unikn::usecol(c(Pinky, Seeblau))) +  # unikn colors
  labs(title = "Outliers relative to both overall sample and gender", 
       x = "Gender", y = "Height (in cm)", 
       fill = "Gender:") +
  theme_bw()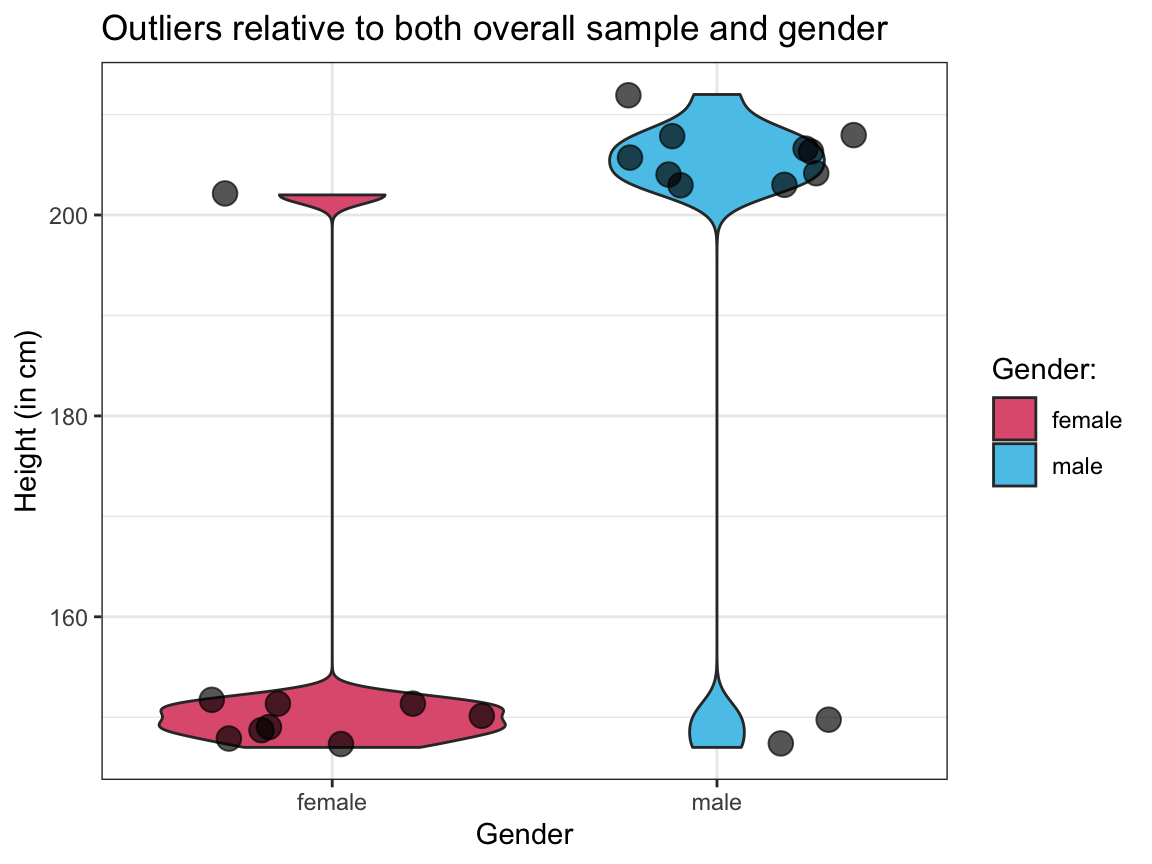


# Interpretation: 
# `out_1` contains mostly short women (except for 1 tall woman) 
#  and mostly tall men (except for 2 short men). 

# 2. Showing out_2: 
ggplot(out_2, aes(x = sex, y = height)) +
  geom_violin(aes(fill = sex)) + 
  geom_jitter(size = 4, alpha = 2/3) + 
  # scale_fill_manual(values = c("firebrick", "steelblue3")) +
  scale_fill_manual(name = "Gender:", values = unikn::usecol(c(Pinky, Seeblau))) +  # unikn colors
  labs(title = "Outliers relative to gender but not overall sample", 
       x = "Gender", y = "Height (in cm)", 
       fill = "Gender:") +
  theme_bw()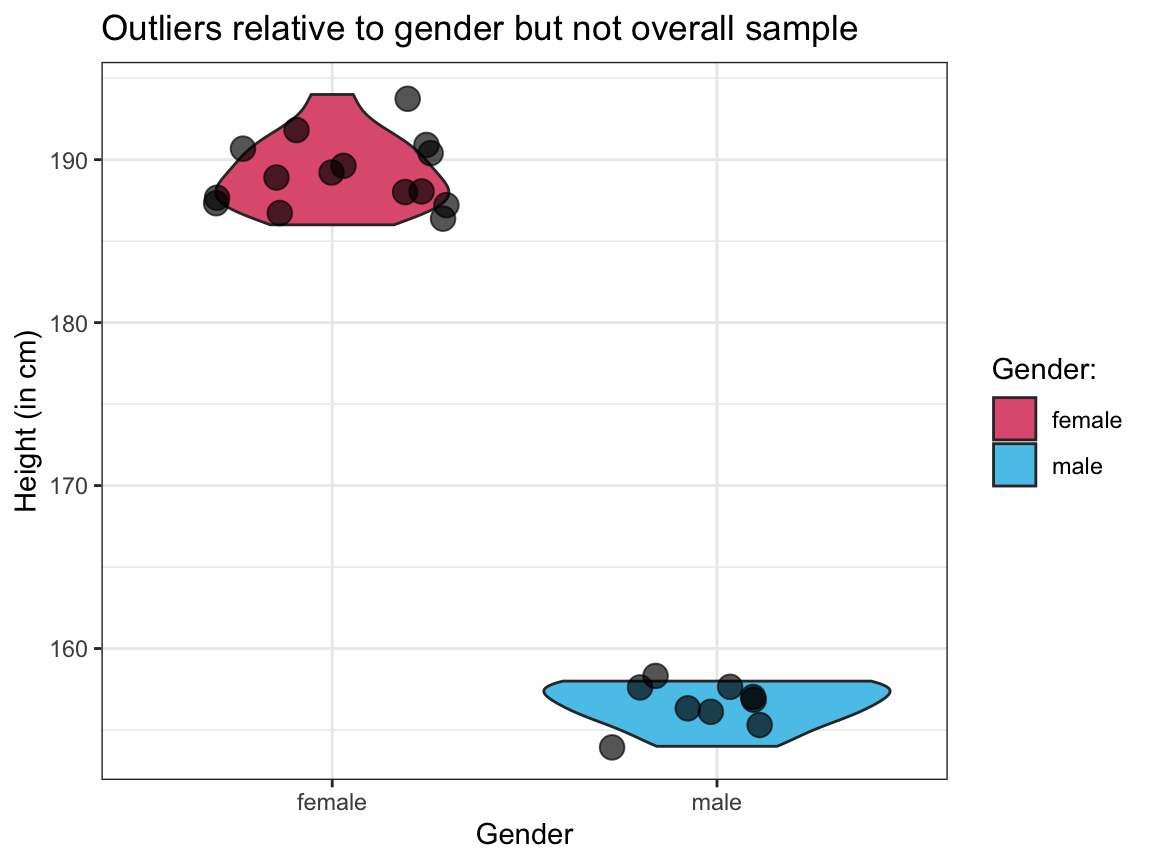


# Interpretation: 
# `out_2` contains individuals which are either tall women or short men.

A.3.5 Exercise 5

Revisiting positive psychology

In previous exercises, we used the p_info data — available as posPsy_p_info in the ds4psy package or as http://rpository.com/ds4psy/data/posPsy_participants.csv — from a study on the effectiveness of web-based positive psychology interventions (Woodworth et al., 2018). More specifically, we used this data in Exercise 6 of Chapter 1 and Exercise 5 of Chapter 2 to explore the participant information and create some corresponding plots. (See Section B.1 of Appendix B for background information on this data.)

Answer the same questions as in those exercises by verifying your earlier base R results and ggplot2 graphs by pipes of dplyr functions. Do your graphs and quantitative results support the same conclusions?

Data

# Data: 
p_info <- ds4psy::posPsy_p_info  # from ds4psy package

## Load data (from online source):
# p_info_2 <- readr::read_csv(file = "http://rpository.com/ds4psy/data/posPsy_participants.csv")

## Verify equality:
# all.equal(p_info, p_info_2)

# p_info
dim(p_info)  # 295 rows, 6 columns
#> [1] 295   6

From Exercise 6 of Chapter 1

Questions from Exercise 6 of Chapter 1:

Examine the participant information in p_info by describing each of its variables:

How many individuals are contained in the dataset?
What percentage of them is female (i.e., has a sex value of 1)?
How many participants were in one of the 3 treatment groups (i.e., have an intervention value of 1, 2, or 3)?
What is the participants’ mean education level? What percentage has a university degree (i.e., an educ value of at least 4)?
What is the age range (min to max) of participants? What is the average (mean and median) age?
Describe the range of income levels present in this sample of participants. What percentage of participants self-identifies as having a below-average income (i.e., an income value of 1)?

Solution

# 1. How many individuals are contained in the dataset? 
N <- nrow(p_info) # OR 
N  # 295
#> [1] 295

# Note: 
p_info %>% count()
#> # A tibble: 1 × 1
#>       n
#>   <int>
#> 1   295
# would yield a tibble (with only 1 element: 295).

# 2. What percentage of them is female (i.e., has a `sex` value of 1)?
p_info %>%
  group_by(sex) %>% 
  summarise(n_sex = n(),            # number 
            pc_sex = n_sex/N * 100  # percentage
            )
#> # A tibble: 2 × 3
#>     sex n_sex pc_sex
#>   <dbl> <int>  <dbl>
#> 1     1   251   85.1
#> 2     2    44   14.9

# 3. How many participants were in one of the 3 treatment groups (i.e., have an `intervention` value of 1, 2, or 3)? 
p_info %>%
  filter(intervention < 4) %>%
  count()  
#> # A tibble: 1 × 1
#>       n
#>   <int>
#> 1   222
# => 222 individuals

# OR: 
t_iv <- p_info %>%
  group_by(intervention) %>% 
  summarise(n_iv = n(),           # number 
            pc_iv = n_iv/N * 100  # percentage
            ) 
t_iv
#> # A tibble: 4 × 3
#>   intervention  n_iv pc_iv
#>          <dbl> <int> <dbl>
#> 1            1    72  24.4
#> 2            2    76  25.8
#> 3            3    74  25.1
#> 4            4    73  24.7
sum(t_iv$n_iv[1:3]) 
#> [1] 222
# => 222 in elements 1:3 of vector n_iv 


# 4. What is the participants' mean education level? 
p_info %>%
  summarise(mn_edu = mean(educ))
#> # A tibble: 1 × 1
#>   mn_edu
#>    <dbl>
#> 1   3.98

# What percentage has a university degree (i.e., an `educ` value of at least 4)?
p_info %>%
  group_by(educ) %>% 
  summarise(n_edu = n(),            # number 
            pc_edu = n_edu/N * 100  # percentage
            ) 
#> # A tibble: 5 × 3
#>    educ n_edu pc_edu
#>   <dbl> <int>  <dbl>
#> 1     1    14   4.75
#> 2     2    21   7.12
#> 3     3    39  13.2 
#> 4     4   104  35.3 
#> 5     5   117  39.7

# 5. What is the age range (`min` to `max`) of participants? 
#    What is the average (mean and median) age?
p_info %>%
  summarise(n = n(),
            min_age = min(age),
            mn_age = mean(age),
            max_age = max(age)) 
#> # A tibble: 1 × 4
#>       n min_age mn_age max_age
#>   <int>   <dbl>  <dbl>   <dbl>
#> 1   295      18   43.8      83

# 6. Describe the range of `income` levels present in this sample of participants. 
#    What percentage of participants self-identifies as a below-average income 
#    (i.e., an `income` value of 1)?
p_info %>%
  group_by(income) %>%
  summarise(n_income = n(),
            pc_income = n_income/N * 100) 
#> # A tibble: 3 × 3
#>   income n_income pc_income
#>    <dbl>    <int>     <dbl>
#> 1      1       73      24.7
#> 2      2      136      46.1
#> 3      3       86      29.2

From Exercise 5 of Chapter 2

Questions from Exercise 5 of Chapter 2:

Use the p_info data to create some plots that descripte the sample of participants:

A histogram that shows the distribution of participant age in 3 ways:
- overall,
- separately for each sex, and
- separately for each intervention.

Solution

When using dplyr instead of ggplot2, we can replace the information contained in the histogram by a table of descriptives:

# Age distribution (as a table): 
age_overall <- p_info %>%
  summarise(n = n(),              # number 
            min_age = min(age),   # minimum
            mn_age = mean(age),   # mean
            md_age = median(age), # median           
            sd_age = sd(age),     # standard deviation
            max_age = max(age)    # maximum
  )
age_overall
#> # A tibble: 1 × 6
#>       n min_age mn_age md_age sd_age max_age
#>   <int>   <dbl>  <dbl>  <dbl>  <dbl>   <dbl>
#> 1   295      18   43.8     44   12.4      83

# Age distribution by sex (as a table): 
age_by_sex <- p_info %>%
  group_by(sex) %>% 
  summarise(n = n(),              # number 
            min_age = min(age),   # minimum
            mn_age = mean(age),   # mean
            md_age = median(age), # median           
            sd_age = sd(age),     # standard deviation
            max_age = max(age)    # maximum
  )
age_by_sex
#> # A tibble: 2 × 7
#>     sex     n min_age mn_age md_age sd_age max_age
#>   <dbl> <int>   <dbl>  <dbl>  <dbl>  <dbl>   <dbl>
#> 1     1   251      19   43.9     44   12.1      83
#> 2     2    44      18   43.0     44   14.1      71

# Age distribution by intervention (as a table): 
age_by_iv <- p_info %>%
  group_by(intervention) %>% 
  summarise(n = n(),              # number 
            min_age = min(age),   # minimum
            mn_age = mean(age),   # mean
            md_age = median(age), # median           
            sd_age = sd(age),     # standard deviation
            max_age = max(age)    # maximum
  )
age_by_iv
#> # A tibble: 4 × 7
#>   intervention     n min_age mn_age md_age sd_age max_age
#>          <dbl> <int>   <dbl>  <dbl>  <dbl>  <dbl>   <dbl>
#> 1            1    72      22   44.6   45     12.1      71
#> 2            2    76      18   45.4   45.5   12.5      83
#> 3            3    74      19   43.3   44     12.2      71
#> 4            4    73      19   41.7   40     12.8      75

A bar plot that
- shows how many participants took part in each intervention; or
- shows how many participants of each sex took part in each intervention.

Solution

Using dplyr instead of ggplot2:

# Number of participants per intervention:
# (was contained in age_by_iv above): 
age_by_iv %>%
  select(intervention, n)
#> # A tibble: 4 × 2
#>   intervention     n
#>          <dbl> <int>
#> 1            1    72
#> 2            2    76
#> 3            3    74
#> 4            4    73

# N and percentage by intervention and sex:
p_info %>%
  group_by(intervention, sex) %>% 
  summarise(n_iv_sex  = n(),              # number 
            pc_iv_sex = n_iv_sex/N * 100  # percentage 
            ) 
#> # A tibble: 8 × 4
#> # Groups:   intervention [4]
#>   intervention   sex n_iv_sex pc_iv_sex
#>          <dbl> <dbl>    <int>     <dbl>
#> 1            1     1       62     21.0 
#> 2            1     2       10      3.39
#> 3            2     1       66     22.4 
#> 4            2     2       10      3.39
#> 5            3     1       62     21.0 
#> 6            3     2       12      4.07
#> 7            4     1       61     20.7 
#> 8            4     2       12      4.07

A.3.6 Exercise 6

Surviving the Titanic

The Titanic data in datasets contains basic information on the Age, Class, Sex, and Survival status for the people on board of the fatal maiden voyage of the Titanic. This data is saved as a 4-dimensional array resulting from cross-tabulating 2201 observations on four variables, but can easily be transformed into a tibble titanic by calling titanic <- as_tibble(datasets::Titanic).

# ?datasets::Titanic  # see documentation  
# dim(Titanic)        # see also dim(FFTrees::titanic)

titanic <- tibble::as_tibble(datasets::Titanic)
knitr::kable(head(titanic), caption = "The head of the Titanic dataset (as a tibble).")

Table A.1: The head of the Titanic dataset (as a tibble).
Class	Sex	Age	Survived	n
1st	Male	Child	No	0
2nd	Male	Child	No	0
3rd	Male	Child	No	35
Crew	Male	Child	No	0
1st	Female	Child	No	0
2nd	Female	Child	No	0

Use dplyr pipes to answer each of the following questions by a summary table that counts the sum of particular groups of survivors.

Determine the number of survivors by Sex: Were female passengers more likely to survive than male passengers?

# Survivors by Sex:
# (a) simple solution:
titanic %>%
  group_by(Sex, Survived) %>%
  summarise(Number = sum(n))
#> # A tibble: 4 × 3
#> # Groups:   Sex [2]
#>   Sex    Survived Number
#>   <chr>  <chr>     <dbl>
#> 1 Female No          126
#> 2 Female Yes         344
#> 3 Male   No         1364
#> 4 Male   Yes         367

# (b) complex solution (computing percentages overall and per subgroup):
t_51 <- titanic %>% 
  group_by(Sex, Survived) %>%
  summarise(nr_all = sum(n),
            pc_all = round(nr_all/sum(titanic$n) * 100, 1)) %>%
  group_by(Sex) %>%
  mutate(nr_sex = sum(nr_all),
         pc_sex  = round(nr_all/nr_sex * 100, 1))
knitr::kable(t_51, caption = "Number of Titanic survivors by `Sex`.")

Table A.2: Number of Titanic survivors by `Sex`.
Sex	Survived	nr_all	pc_all	nr_sex	pc_sex
Female	No	126	5.7	470	26.8
Female	Yes	344	15.6	470	73.2
Male	No	1364	62.0	1731	78.8
Male	Yes	367	16.7	1731	21.2


# Corresponding Chi-square test:
tab_2x2 <- xtabs(n ~ Survived + Sex, titanic)
tab_2x2
#>         Sex
#> Survived Female Male
#>      No     126 1364
#>      Yes    344  367
csq_tst <- chisq.test(tab_2x2, correct = FALSE)
csq_tst
#> 
#>  Pearson's Chi-squared test
#> 
#> data:  tab_2x2
#> X-squared = 456.87, df = 1, p-value < 2.2e-16
csq_tst$expected
#>         Sex
#> Survived   Female      Male
#>      No  318.1736 1171.8264
#>      Yes 151.8264  559.1736
csq_tst$observed
#>         Sex
#> Survived Female Male
#>      No     126 1364
#>      Yes    344  367

Answer: Yes, the variables Sex and Survived are related. Whereas females were about three times as likely to survive than to die, males were about four times as likely to die than to survive.

Determine the number of survivors by Age: Were children more likely to survive than adults?

# Survivors by Age:
# (a) simple solution:
titanic %>%
  group_by(Age, Survived) %>%
  summarise(Number = sum(n))
#> # A tibble: 4 × 3
#> # Groups:   Age [2]
#>   Age   Survived Number
#>   <chr> <chr>     <dbl>
#> 1 Adult No         1438
#> 2 Adult Yes         654
#> 3 Child No           52
#> 4 Child Yes          57

# (b) complex solution (computing percentages overall and per subgroup):
t_52 <- titanic %>% 
  group_by(Age, Survived) %>%
  summarise(nr_age_sur = sum(n),
            pc_age_sur = round(nr_age_sur/sum(titanic$n) * 100, 1)) %>%
  group_by(Age) %>%
  mutate(nr_age = sum(nr_age_sur),
         pc_age  = round(nr_age_sur/nr_age * 100, 1))
knitr::kable(t_52, caption = "Number of Titanic survivors by `Age`.")

Table A.3: Number of Titanic survivors by `Age`.
Age	Survived	nr_age_sur	pc_age_sur	nr_age	pc_age
Adult	No	1438	65.3	2092	68.7
Adult	Yes	654	29.7	2092	31.3
Child	No	52	2.4	109	47.7
Child	Yes	57	2.6	109	52.3


# Corresponding Chi-square test:
tab_2x2 <- xtabs(n ~ Survived + Age, titanic)
tab_2x2
#>         Age
#> Survived Adult Child
#>      No   1438    52
#>      Yes   654    57
csq_tst <- chisq.test(tab_2x2, correct = FALSE)
csq_tst
#> 
#>  Pearson's Chi-squared test
#> 
#> data:  tab_2x2
#> X-squared = 20.956, df = 1, p-value = 4.701e-06
csq_tst$expected
#>         Age
#> Survived     Adult    Child
#>      No  1416.2108 73.78919
#>      Yes  675.7892 35.21081
csq_tst$observed
#>         Age
#> Survived Adult Child
#>      No   1438    52
#>      Yes   654    57

Answer: Yes, the variables Age and Survived are related. Whereas adults were more than twice as likely to die than to survive, the chances of survival for children were almost 50%.

Consider the number of survivors as a function of both Sex and Age. Does the pattern observed in 1. hold equally for children and adults?

# Survivors by Age and Sex:
t_53 <- titanic %>% 
  group_by(Age, Sex, Survived) %>%
  summarise(nr_age_sex_sur = sum(n),
            pc_age_sex_sur = round(nr_age_sex_sur/sum(titanic$n) * 100, 1)) %>%
  group_by(Age, Sex) %>%
  mutate(nr_age_sex = sum(nr_age_sex_sur),
         pc_age_sex = round(nr_age_sex_sur/nr_age_sex * 100, 1))

knitr::kable(t_53, caption = "Number of Titanic survivors by `Age` and `Sex`.")

Table A.4: Number of Titanic survivors by `Age` and `Sex`.
Age	Sex	Survived	nr_age_sex_sur	pc_age_sex_sur	nr_age_sex	pc_age_sex
Adult	Female	No	109	5.0	425	25.6
Adult	Female	Yes	316	14.4	425	74.4
Adult	Male	No	1329	60.4	1667	79.7
Adult	Male	Yes	338	15.4	1667	20.3
Child	Female	No	17	0.8	45	37.8
Child	Female	Yes	28	1.3	45	62.2
Child	Male	No	35	1.6	64	54.7
Child	Male	Yes	29	1.3	64	45.3

Answer: Female adults have a higher chance of survival than male adults (74.4% vs. 20.3%) and female children have a higher chance of survival than male children (62.2% vs. 45.3%, respectively). However, the relative advantage for being female rather than male is much higher for adults (as the survival chances of female adults are 54.1% percentage points higher than for male adults) than for children (as the survival chance of female children are only 16.9% percentage points higher than for male children). Thus, being female was more of an advantage for adults than for children (and the survival rate of female adults was higher than the survival rate for children of either sex).

Statistically, this suggests an interaction between the factors Age and Sex on the chances of survival, though note that there were only 109 children overall (i.e., 4.95% of the passenger population).

The documentation of the Titanic data suggests that the policy women and children first was “not entirely successful in saving the women and children in the third class”. Verify this by creating corresponding contingency tables (i.e., counts of survivors).

# Survivors by Sex for each class:
t_54a <- titanic %>% 
  # filter(Class == "3rd") %>%
  group_by(Class, Sex, Survived) %>%
  summarise(count = sum(n), 
            pc = round(count/sum(titanic$n) * 100, 2))
knitr::kable(t_54a, caption = "Number of Titanic survivors by `Class` and `Sex`.")

Table A.5: Number of Titanic survivors by `Class` and `Sex`.
Class	Sex	Survived	count	pc
1st	Female	No	4	0.18
1st	Female	Yes	141	6.41
1st	Male	No	118	5.36
1st	Male	Yes	62	2.82
2nd	Female	No	13	0.59
2nd	Female	Yes	93	4.23
2nd	Male	No	154	7.00
2nd	Male	Yes	25	1.14
3rd	Female	No	106	4.82
3rd	Female	Yes	90	4.09
3rd	Male	No	422	19.17
3rd	Male	Yes	88	4.00
Crew	Female	No	3	0.14
Crew	Female	Yes	20	0.91
Crew	Male	No	670	30.44
Crew	Male	Yes	192	8.72


# Survivors by Age for each class:
t_54b <- titanic %>% 
  # filter(Class == "3rd") %>%
  group_by(Class, Age, Survived) %>%
  summarise(count = sum(n), 
            pc = round(count/sum(titanic$n) * 100, 2))
knitr::kable(t_54b, caption = "Number of Titanic survivors by `Class` and `Age`.")

Table A.5: Number of Titanic survivors by `Class` and `Age`.
Class	Age	Survived	count	pc
1st	Adult	No	122	5.54
1st	Adult	Yes	197	8.95
1st	Child	No	0	0.00
1st	Child	Yes	6	0.27
2nd	Adult	No	167	7.59
2nd	Adult	Yes	94	4.27
2nd	Child	No	0	0.00
2nd	Child	Yes	24	1.09
3rd	Adult	No	476	21.63
3rd	Adult	Yes	151	6.86
3rd	Child	No	52	2.36
3rd	Child	Yes	27	1.23
Crew	Adult	No	673	30.58
Crew	Adult	Yes	212	9.63
Crew	Child	No	0	0.00
Crew	Child	Yes	0	0.00

Answer: Both regularities (i.e., much higher survival chance of females and for children) are lower for 3rd class passengers (despite still showing the same trends).

This concludes our exercises on dplyr — but the topic of data transformation will stay relevant throughout this book.

References

Woodworth, R. J., O’Brien-Malone, A., Diamond, M. R., & Schüz, B. (2018). Data from “Web-based positive psychology interventions: A reexamination of effectiveness”. Journal of Open Psychology Data, 6(1). https://doi.org/10.5334/jopd.35

A.3 Solutions (03)

A.3.1 Exercise 1

Reshaping vs. reducing data

Solution

A.3.2 Exercise 2

Star and R wars

Known unknowns

Solution

Gender issues

Solution

Solution

Popular homes and heights

Solution

Size and mass issues

Solution

Bonus tasks

Solution

A.3.3 Exercise 3

Sleeping mammals

Solution

Arranging and filtering data

Solution

Computing new variables

Solution

A.3.4 Exercise 4

Outliers

Data on outliers

Not all outliers are alike

Basic tasks

Solution

Defining different outliers

Relative outliers

Solution

Bonus plots

Solution

A.3.5 Exercise 5

Revisiting positive psychology

Data

From Exercise 6 of Chapter 1

Solution

From Exercise 5 of Chapter 2

Solution

Solution

A.3.6 Exercise 6

Surviving the Titanic

References

Data on `outliers`