Capítulo 3 Contraste de hipótesis

En la última unidad hemos hablado sobre los conceptos detrás de la estimación, que es uno de los dos “grandes temas” en la estadística inferencial. Ahora es tiempo de centrar nuestra atención en el otro gran tema, que es el contraste de hipótesis. En su forma más abstracta, el contraste de hipótesis es una idea muy simple: el investigador tiene una teoría sobre el mundo, y quiere determinar si los datos apoyan o no su teoría. Sin embargo, los detalles detrás del contraste de hipótesis son un poco más complicados, y mucha gente encuentra frustrante esta parte de la estadística. Aquí, intentaremos que no lo sean tanto. La estructura de esta unidad será la siguiente. Primero, describiré como funciona el contraste de hipótesis con algo de detalle, utilizando un ejemplo que mostrará como se “construye” un test estadístico. Evitaré ser muy dogmático y me enfocaré más bien en la lógica que hay detrás de este procedimiento..⁵ Después, destinaré unas líneas para hablar sobre algunos dogmas, reglas y “herejías” alrededor de la teoría del contraste de hipótesis.

3.1 Un montón de hipótesis

Algún día, en un futuro muy distante, quizás triunfe como profesor y consiga ser catedrático. En ese hipotético escenario, podré relajar mi calendario docente y podré finalmente dedicarme a la línea de investigación más improductiva que existe: la búsqueda de la percepción extrasensorial (PES).⁶

Supongamos que por fin me llega ese día. Mi primer estudio, será necesariamente uno sencillo, y con él buscaré demostrar que la telepatía existe. Cada uno de los participantes de mi estudio estará sentado frente a una mesa donde el experimentador le mostrará una carta. Esta carta es negra por un lado y blanca por el otro. Después, el experimentador retirará la carta y la colocará en una mesa en una habitación adyacente. Entonces, un segundo experimentador entrará y le pedirá al participante que diga de qué lado de la carta está boca arriba. Sólo tendrá una oportunidad. Cada persona verá únicamente una carta y dará una sola respuesta; en ningún momento el participante estará en contacto con alguien que conozca la respuesta correcta. Mis datos, por lo tanto, serán muy simples. He preguntado a un número $N$ de personas y un número $X$ de personas acertará. Para ser concretos, he evaluado a $N = 100$ participantes, de los cuales $X = 62$ han respondido correctamente… Esta es una cifra alta (recuerda que la probabilidad de acertar al azar era del 50%) pero, ¿es lo suficientemente alta como para declarar que hemos encontrado evidencia de que el PES existe? Es en este tipo de escenarios donde el contraste de hipótesis es útil. Sin embargo, antes de hablar sobre cómo podemos probar esas hipótesis, necesitamos aclarar a qué nos referimos exactamente por hipótesis.

3.1.1 Hipótesis de investigación vs. hipótesis estadísticas

La primera distinción que necesitas tener absolutamente clara es la que hay entre una hipótesis de investigación y una hipótesis estadística. En mi estudio de PES, mi meta cientifíca es demostrar que la telepatía existe. Bajo este escenario, mi meta de investigación es clara: espero obtener evidence de que existe el PES. En otras situaciones podrías ser un poco más neutral y decir que mi meta de investigación es determinar si existe o no la telepatía (aunque lo parece, ambas metas no representan exactamente lo mismo). De cualquier forma, el punto al que quiero llegar es que una hipótesis de investigación significa hacer una declaración científica demostrable y sustantiva… en el caso de un educador, estas hipótesis de investigación serán sobre estilos o herramientas educativas como en los siguientes ejemplos:

Escuchar música reduce tu habilidad de prestar atención a otras cosas. Este es un argumento sobre la relación causal que existe entre dos conceptos significativos (escuchar música y prestar atención a cosas), por lo que es una hipótesis de investigación válidad.
La inteligencia está relacionada con la personalidad. Como en la hipótesis anterior, se trata de un argumento relacional entre dos conceptos (inteligencia y personalidad), pero es más débil: asume que entre las dos existe una relación y no necesariamente que una cause a la otra.

Como podrás observar, estas hipótesis de investigación pueden solaparse unas con otras. Mi objetivo final en el experimento PES podría ser comprobar si “la PES existe”, pero quizás tenga que restringir operacionalmente mi hipótesis a algo como “algunas personas pueden ‘ver’ objetos, como si fueran videntes”. Dicho esto, existen algunas cosas que no cuentan como hipótesis de investigación:

El amor es un misterio. Esto es muy ambiguo para ser comprobable. Aunque es posible que una hipótesis de investigación contenga algo de ambigüedad, tiene que ser operacionalizable (que pueda ser medida a través de algún instrumento). Es demasiado complicado pensar en una forma de medir lo que “son” el amor y misterio, como para después poder compararlos.
En mi experimento, más personas dirán “sí” que “no”. Este argumento falla ya que hace referencia a un tipo de respuesta que quedará registrado en los datos del estudio, y no al concepto o pregunta original del estudio.

Como podrás ver, las hipótesis de investigación pueden ser un poco complicadas a veces, y a final se tratan de afirmaciones científicas. Las hipótesis estadísticas, por otro lado, no son ninguna de estas dos cosas. Las hipótesis estadísticas deben de ser precisas matemáticamente hhablando y deben ajustarse a las características del mecanismo que genera los datos (por ejemplo, la “población”). La intención es que las hipótesis estadísticas muestren una relación clara y sustancial con las hipótesis de investigación que se busca resolver. Así, en mi estudio sobre la PES mi hipótesis de investigación es que algunas personas son capaces de ver el futuro, o algo así. Entonces, lo que debería hacer trasladar esta idea a una afirmación sobre cómo se producen los datos. Pensamos un momento cómo debería de ser esta afirmación. Usaremos la letra griega $\theta$ (theta) para referirnos a esta probabilidad. Te presento cuatro hipótesis estadísticas diferentes:

Si la PES no existe y mi experimento está bien diseñado, entonces mis participantes están adivinando. Por lo tanto, esperaría que acierten la mitad de las veces con lo que mi hipótesis estadística sería que la probabilidad de escoger correctamente es $\theta = 0.5$.
Alternativamente, supongamos que la PES sí existe y que los participantes pueden ver la carta. Si esto es verdad, los participantes tendrán un mejor rendimiento que el azar (>50%). Así, la hipótesis estadística sería que $\theta > 0.5$.
Una tercera posibilidad es que la PES exista, pero que los colores de las cartas están invertidos y los participantes no lo saben, por lo que esperaríamos un resultado menor que el azar (esto es un poco enrevesado, pero en el mundo de la posibilidades, existe). Aquí la hipótesis estadística sería que $\theta < 0.5$.
Finalmente, supongamos que la PES existe pero no tengo idea si los participantes están viendo el color correcto o no. En este caso, la única afirmación que puedo hacer sobre los datos es que la probilidad de escoger correctamente no es igual al 50%. Esto corresponde con la hipótesis estadística $\theta \neq 0.5$.

Todas son ejemplos de hipótesis estadísticas legítimas porque son argumentos sobre un parámetro poblacional (número de cartas correctamente identificadas) y están significativamente relacionados con mi experimento (saber si la PES existe).

Lo que esta discusión deja en claro, espero, es que cuando intentamos construir un test estadístico sobre una hipótesis, el investigador tiene que tener dos hipótesis diferentes que considerar: una hipótesis de investigación y su correspondiente hipótesis estadística. En el ejemplo de la PES sería que:

Hipótesis.de.Investigación	Hipótesis.Estadística
PES.existe	$\theta \neq 0.5$

El aspecto clave a reconocer es el siguiente: un test estadístico es un test hipótesis estadísticas, no hipótesis de investigación. Si tu estudio no está bien diseñado, entonces el vínculo entre tu hipótesis de investigación y tu hipótesis estadística se rompe. Poniendo un ejemplo simplista, supongamos que estudio sobre la PES lo hacemos de tal forma que los participantes puedan ver la carta reflejada en una ventana; si eso pasa, podría encontrar evidencia clara y contundente de que $\theta \neq 0.5$, sin embargo, esto no nos dirá nada sobre si “la PES existe”.

3.1.2 Hipótesis nula e hipótesis alternativa

Recapitulemos brevemente. Tengo una hipótesis de investigación que corresponde con alguna creencia que tengo sobre el mundo que puedo traducir en una hipótesis estadística que corresponde con mi creencia sobre cómo se generaron esos datos. A partir de aquí se complican las cosas para muchas personas. Y esto es porque el siguiente paso consiste en inventar una nueva hipótesis estadística (la hipótesis “nula”, $H_0$) que corresponde con exactamente lo opuesto a lo que quiero creer, y después enfocarnos exclusivamente en ella casi al punto de olvidarnos de lo que es nuestra hipótesis estadística original (que ahora llamaremos hipótesis “alternativa”, $H_1$). En nuestro ejemplo de la PES, la hipótesis nula es que $\theta = 0.5$, ya que es lo que esperaríamos si la PES no existiese. Mi esperanza, por supuesto, es que la PES sea real, por lo que la alternativa a esta hipótesis nula es que $\theta \neq 0.5$. En esencia, lo que estamos haciendo es dividir los valores posibles de $\theta$ en dos grupos: aquellos valores que esperamos que no sean verdaderos (la nula), y aquellos valores con los que estaríamos felices que ocurrieran (la alternativa). Es importante reconocer que el objetivo de un test de contraste de hipótesis no es mostrar que la hipótesis alternativa es (probablemente) verdad; nuestro objetivo es demostrar que la hipótesis nula es (probablemente) falsa.

La mejor forma de ilustrar esta idea es imaginar que el contraste de hipótesis es como un juicio penal… el juicio de la hipótesis nula. La hipótesis nula es la defensa, y el investigador es el fiscal, mientras que el test estadístico es el juez. Al igual que en un juicio penal, existe la presunción de inocencia: la hipótesis nula es considerada como verdad a menos que tú, el investigador, demuestre más allá de toda duda razonable que es falsa. Tú eres libre de diseñar el experimento de cualquier forma y tu objetivo es diseñarlo de tal forma que maximice la probabilidad de que los datos producidos demuestren que la hipótesis nula es falsa. El truco está en que el test estadístico -el juez- determina cuáles son las reglas del juicio, y esas reglas están diseñadas para proteger a la hipótesis nula – específicamente para que, en caso de que la hipótesis nula sea verdad, se garantice que las probabilidad de una “condena” equivocada sean las mínimas (como en un juicio de verdad). Esto es muy importante: después de todo, la hipótesis nula no tiene un abogado, y como el investigador está intentando demostrar que el falsa a como de lugar, alguien tiene que defenderla.

3.2 Dos tipos de error

Antes de entrar en detalles sobre cómo se construye un test estadístico, es útil entender la filosofía que hay detrás de ella. Ya he dado algunas pistas al comparar el contraste hipótesis con un juicio penal, pero ahora seremos más explícitos. Idealmente, nos gustaría construir un test que nunca cometa errores. Desafortudamente, la realidad y sus elementos son muy variables, por lo que esto es imposible. A veces, simplemente tenemos mala suerte: imagina que al lanzar una moneda 10 veces seguidas obtienes como resultado 10 caras. Esto parece evidencia sólida de que la moneda está sesgada (¡y lo es!), pero es evidente que existe 1 sobre 1024 posibilidades de que esto pase aún cuando la moneda sea completamente justa. En otras palabras, en la vida real siempre habrá que aceptar que existe la posibilidad de haberlo hecho mal. Como consecuencia, el objetivo detrás de un test estadístico no es eliminar los errores, sino *minimizarlos.

Llegados a este punto necesitamos ser más precisos y definir qué queremos decir por “error”. En primer lugar, lo obvio: la hipótesis nula o es verdadera o es falsa; y nuestro test será capaz de decirnos si rechaza la hipótesis nula o la mantiene.⁷ Como la siguiente tabla ilustra, al hacer un test y tomar una decisión, podremos obtener uno de los cuatro siguientes resultados:

	mantengo $H_0$	rechazo $H_0$
$H_0$ es verdadera	decisión correcta	error (tipo I)
$H_0$ es falsa	error (tipo II)	decisión correcta

Vemos como en realidad existen dos tipos de error. Si rechazamos la hipótesis nula pero es verdadera, entonces hemos hecho un error de tipo I. Por otro lado, si mantenemos la hipótesis nula cuando es falsa, entonces habremos cometido un error de tipo II.

¿Recuerdas que un contraste de hipótesis es como un juicio penal? Un juicio penal requiere que establezcas “más alla de toda duda razonable” que el acusado es culpable. Las reglas sobre el tipo de evidencia (en teoría) están diseñadas para asegurar que no existe (prácticamente) ninguna posibilidad de condenar equivocadamente a un inocente. El juicio está diseñado para defender los derechos del acusado: es mejor que diez culpables queden libres a que un inocente sufra. En otras palabras, un juicio penal no trata a los dos tipos de error de la misma forma… castigar al inocente se considera peor a dejar libre al culpable. En un test estadístico la situación es parecida: la aspecto más importante en el diseño de un test es controlar la probabilidad de cometer un error de tipo I, manteniéndolo debajo de una probabilidad preestablecida. Esta probabilidad, denotada como $\alpha$, se denomina como el nivel de significación de un test. Así, se dice un test estadístico tiene un nivel de significación $\alpha$ si el error de tipo I es menor que $\alpha$.

¿Y qué pasa con el error de tipo II? En realidad, también nos gustaría tenerlo bajo control, y denotamos esta probabilidad como $\beta$. Sin embargo, es mucho más común referirnos a él como el poder del test, que es la probabilidad con la que rechazamos una hipótesis nula cuando en realidad es falsa, que se obtiene al resta $1-\beta$. Para seguir la línea, actualizo la tabla anterior agregando los números relevanetes:

	retener $H_0$	rechazar $H_0$
$H_0$ es verdadera	$1-\alpha$ (probabilidad de retener correctamente)	$\alpha$ (error de tipo I)
$H_0$ es falsa	$\beta$ (error de tipo II)	$1-\beta$ (poder del test)

Un test estadístico “efectivo” es aquel que tenga un valor pequeño de $\beta$, a la vez que mantiene fijo un valor (bajo) de $\alpha$. Por convención, los científicos suelen utilizar tres niveles de $\alpha$: $.05$, $.01$ y $.001$. Observa la simetría que hay ahí… los tests están diseñados para asegurar que el nivel de $\alpha$ se mantenga bajo, pero no existe una garantía en relación con el valor de $\beta$. Nos gustaría que el error de tipo II se mantenga pequeño, e intentamos diseñar los test de manera que esto sea así, sin embargo, esto es secundario al compararlo con la necesidad de controlar el error de tipo I. Por lo tanto, bajo esta forma de pensar “es mejor retener 10 hipótesis nulas falsas que rechazar una sola que sea verdadera”. Aunque esta forma de pensar no es la ideal en todos los escenarios, es útil y, sobre todo, continua siendo el paradigma predominante al contrastar hipótesis en la experimentación científica.

3.3 Tests estadísticos y estadísticos muestrales

Visto el concepto que hay detrás de los tests estadísticos, ahora veamos cómo se construye uno. Para ello, volveremos a nuestro ejemplo de la PES. Dejaremos de lado, por un momento, los datos y pensaremos sobre la estructura del experimento. Independientemente de cuáles sean las cifras reales, la forma de los datos es que $X$ de un total de $N$ personas son capaces de identificar el color correcto de la carta oculta. Ahora, supongamos que la hipótesis nula es verdadera: la PES no existe, y la probabilidad de que algún participante escoja el color correcto es exactamente $\theta = 0.5$. ¿Cómo esperaríamos que fueran esos datos? Evidentemente, esperaríamos que la proporción de participantes que responden correctamente sea cerca al 50%. O, poniéndolo en términos matemáticos, diríamos que $X/N$ es aproximadamente $0.5$. Está claro que no esperaríamos que fuera exactamente 0.5: si, por ejemplo, evaluamos a $N=100$ personas y $X = 53$ de ellos responden correctamente, probablemente concederíamos que los datos son consistentes con la hipótesis nula. Por otro lado, si $X = 99$ de nuestros participantes aciertan, estaríamos bastante seguros de que la hipótesis nula es incorrecta. De la misma forma que si $X=3$ personas responden correctamente, estaríamos igualmente seguros de que la hipótesis nula es incorrecta. Siendo un poco más técnicos: tenemos una cantidad $X$ que podemos calcular a partir de nuestros datos; después de mirar el valor de $X$, tomamos una decisión sobre si creer que la hipótesis nula es correcta, o para rechazar la hipótesis nula, en favor de la alternativa. El nombre de este cálculo que necesitamos para guiar nuestras decisiones es un estadístico de test.

Una vez calculado ese estadístico de test, el siguiente paso es establecer de manera precisa, queé valores de ese estadístico van a hacer que rechacemos la hipótesis nula y qué valores van a hacer que la retengamos. Para conseguirlo, debemos determina cuál es la distribución muestral del estadístico de test si la hipótesis nula fuera verdadera (ya hemos hablado de distribuciones muestrales en el Capítulo 2.3.1). ¿Por qué necesitamos esto? Porque una distribución nos dirá exactamente qué valores de $X$ podríamos esperar de la hipótesis nula. En consecuencia, podremos utilizar esa distribución como una herramienta para evaluar que tanto coinciden los valores de la hipótesis nula con nuestros datos.

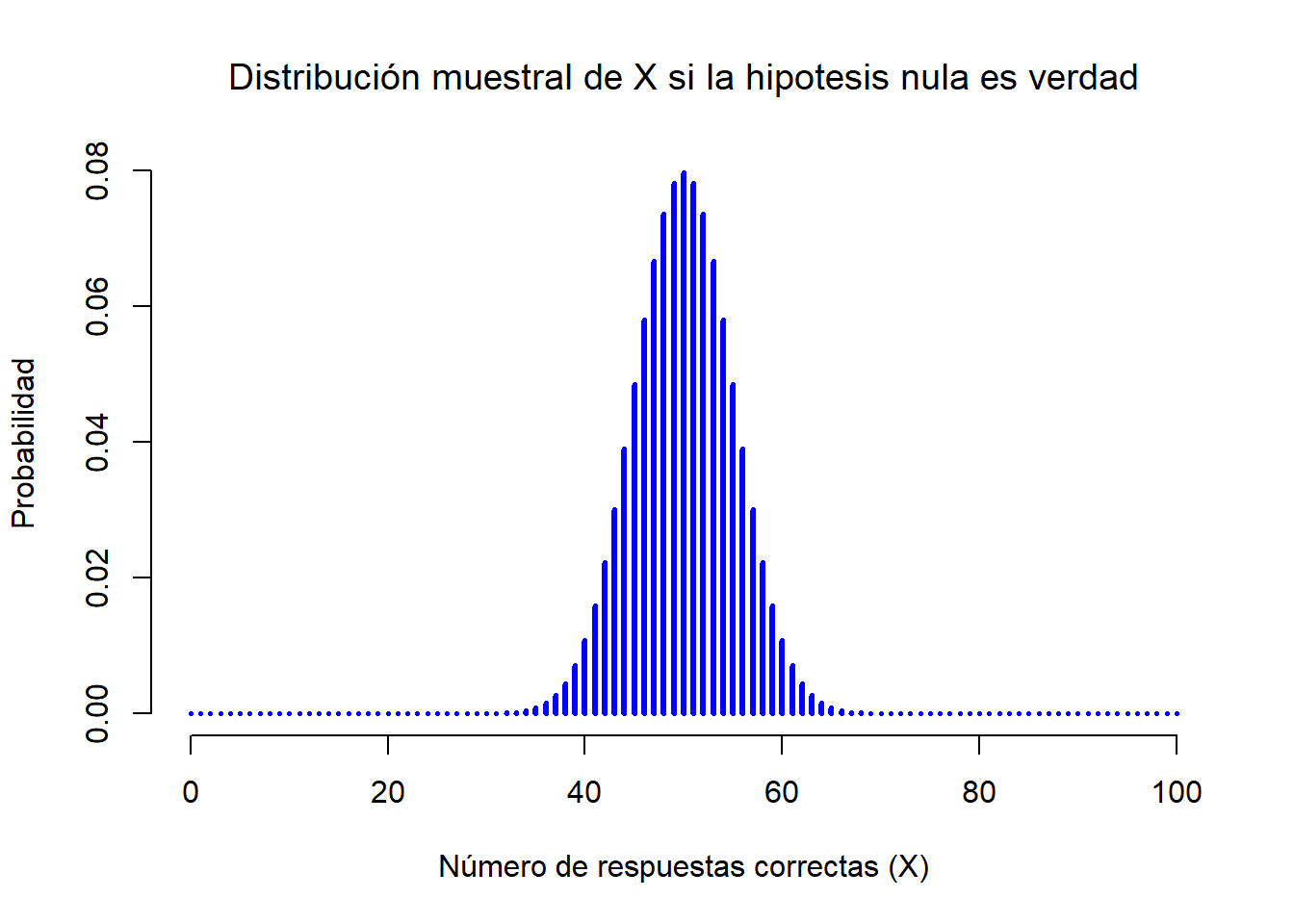
$La distribución muestral para nuestro estadísitco de test $X$ cuando la hipótesis nula es verdadera. En el experimento de la PES, esta es una distribución binomial. Esto no nos debería sorprender ya que si la hipótesis nula dice que la probilidad de una respuesta correcta es de $\theta = .5$, la distribución muestral nos mostrará que el valor más probable es 50 (del total 100) respuesta correctas. Observa como la mayor parte de la densidad de probabilidad está entre 40 y 60.$

Figure 3.1: La distribución muestral para nuestro estadísitco de test $X$ cuando la hipótesis nula es verdadera. En el experimento de la PES, esta es una distribución binomial. Esto no nos debería sorprender ya que si la hipótesis nula dice que la probilidad de una respuesta correcta es de $\theta = .5$, la distribución muestral nos mostrará que el valor más probable es 50 (del total 100) respuesta correctas. Observa como la mayor parte de la densidad de probabilidad está entre 40 y 60.

¿Cómo determinamos qué distribución muestral le corresponde a un estadístico de test? Para muchos contrastes de hipótesis este paso es un poco complicado. Sin embargo, a veces puede ser muy sencillo. Y afortunadamente para nosotros, en nuestro ejemplo de la PES podremos ver uno de los casos más sencillos. Nuestro parámetro poblacional $\theta$ es simplemente la probabilidad de que la gente responda correctamente cuando se le pregunta, y nuestro estadístico de test $X$ es la cuenta del número de personas que lo hicieron, a partir de muestra de tamaño $N$. Ya hemos visto una distribución como esta en el Capítulo 1.4: es una distribución binomial. Usando la notación y terminología introducida al inicio de este Capítulo, podemos decir que la hipótesis nula predice que $X$ está distribuída binomialmente, lo cual se escribe

\[ X \sim \mbox{Binomial}(\theta,N) \]

Ya que la hipótesis nula nos dice que $\theta = 0.5$ y en nuestro experimento hay $N=100$ participantes, tenemos la distribución muestral que necesitamos. Esta distribución muestral se ilustra en la Figura 3.1. No hay ninguna sorpresa: la hipótesis nula dice que $X=50$ es el resultado más probable, y nos dice con cierta seguridad que observaremos entre 40 y 60 respuestas correctas.

3.4 Tomando decisiones

Vale, estamos casi a punto de terminar. Hemos construído un estadístico de test ($X$), y lo hemos escogido de tal forma que estamos bastante seguro que si $X$ se acerca a $N/2$ entonces retendremos a la hipótesis nula, y si no, la rechazamos. Lo que nos queda por saber es lo siguiente: ¿exactamente qué valores del estadístico de test debemos asociar a la hipótesis nula y qué valores a la hipótesis alternativa? En el estudio de la PES, por ejemplo, observamos un valor de $X=62$. ¿Qué decisión hemos de tomar? ¿Deberíamos escoger la hipótesis nula o la hipótesis alternativa?

3.4.1 Regiones críticas y valores críticos

Para responder a esta pregunta, vamos a introducir el concepto de región crítica para el estadístico de test $X$. La región crítica de un estadístico corresponde con aquellos valores de $X$ que nos llevarán a rechazar la hipótesis nula (razón por la cual a esta región crítica también se le llama región de rechazo). ¿Cómo encontramos esta región crítica? Recordemos lo que ya sabemos:

$X$ deberá ser muy grande o muy pequeña para poder rechazar la hipótesis nula.
Si la hipótesis nula es verdadera, la distribución muestral de $X$ es Binomial$(0.5, N)$.
Si $\alpha =.05$, la región crítica deberá cubrir un 5% de la distribución muestral.

Es importante comprender este último punto: la región crítica corresponder con aquellos valores de $X$ con los que rechazaríamos la hipótesis nula, y que la distribución muestral en cuestión describe la probabilidad de obtener un valor específico de $X$ si la hipótesis nula es de hecho verdadera. Ahora, supongamos que escogemos una región crítica que cubre un 20% de la distribución muestral, y supongamos que la hipótesis nula es verdadera. ¿Cuál sería la probabilidad de rechazar incorrectamente la hipótesis nula? La respuesta, por supuesto, es del 20%. Y por lo tanto, habremos construído un test con un nivel de $\alpha$ de $0.2$. Si queremos un $\alpha = .05$, la región crítica sólo tendrá permitido cubrir un 5% de la distribución muestral de nuestro estadístico de test.

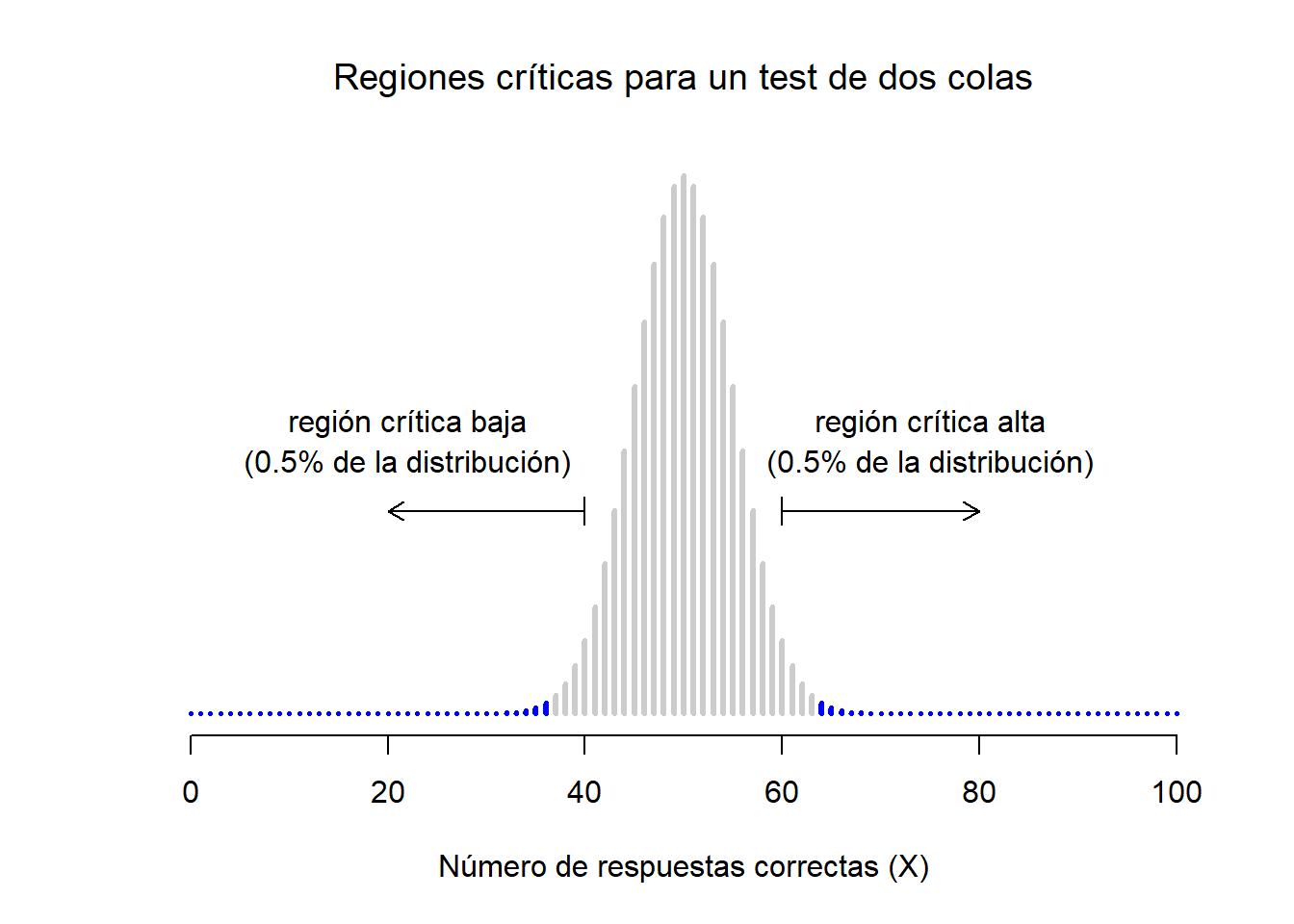
$Región crítica asociada con el contraste de hipótesis de estudio de la PES, con un nivel $\alpha = .05$. La gráfica muestra la distribución de $X$ bajo la hipótesis nula: las barras grises corresponden con los valores de $X$ con los que se podrá retener la hipotesis nula. Las barras negras muestran la región crítica: los valores de $X$ que rechazarán la hipótesis nula. Ya que la hipótesis alternativa tiene dos lados (permite $\theta <.5$ y $\theta >.5$), la región crítica cubre ambas colas de la distribución. Para asegurar un valor $\alpha$ de $.05$, necesitamos asegurar que cada una de las dos regiones comprenda un 2.5% de la distribución muestral.$

Figure 3.2: Región crítica asociada con el contraste de hipótesis de estudio de la PES, con un nivel $\alpha = .05$. La gráfica muestra la distribución de $X$ bajo la hipótesis nula: las barras grises corresponden con los valores de $X$ con los que se podrá retener la hipotesis nula. Las barras negras muestran la región crítica: los valores de $X$ que rechazarán la hipótesis nula. Ya que la hipótesis alternativa tiene dos lados (permite $\theta <.5$ y $\theta >.5$), la región crítica cubre ambas colas de la distribución. Para asegurar un valor $\alpha$ de $.05$, necesitamos asegurar que cada una de las dos regiones comprenda un 2.5% de la distribución muestral.

Así, estas tres cosas nos ayudan a resolver nuestro problema: la región crítica está compuesta por los valores más extremos, conocidos como las colas de la distribución. Esto se ilustra en la Figura 3.2. De esta forma, si quieres que $\alpha = .05$, entonces nuestras regiones críticas corresponderán con $X \leq 40$ y $X \geq 60$.⁸. Esto quiere decir que el número de personas que dice “verdadero” está entre 41 y 59 (ambos inclusive), entonces retendremos la hipótesis nula. Si el número está entre 0 y 40 o entre 60 y 100, entonces rechazaremos la hipótesis nula. En este caso, los números 40 y 60 suelen ser denominados como los valores crítico ya que definen los límites o bordes de la región crítica.

Llegados a este punto, hemos esencialmente completado nuestro contraste de hipótesis: (1) hemos escogido un nivel $\alpha$ (por ejemplo, $\alpha = .05$), (2) hemos creado un estadístico de test (por ejemplo, $X$) que nos permite comparar a $H_0$ con $H_1$, (3) hemos obtenido la distribución muestral de nuestro estadísitco de test, bajo la suposición de que la hipótesis nula es verdadera (en este caso binomial) y finalmente (4) hemos calculado la región crítica para nuestro nivel de $\alpha$ (0-40 y 60-100). Lo único que nos falta es calcular el valor del estadístico de test para los datos reales que disponemos (por ejemplo, $X = 62$) y compararlo con los valores críticos para así poder tomar una decisión. Ya que 62 es mayor que el valor crítico de 60, rechazamos la hipótesis nula o decimos que nuestro contraste de hipótesis ha producido un resultado estadísticamente significativo.

3.4.2 Una nota sobre lo estadísticamente “significativo”

Como en las técnicas ocultas de la adivinación, la estadística tiene su jerga privada ideada deliberadamente para ocultar sus métodos a los no practicantes.

Haremos una pequeña acotación en relación con la palabra “significativo”. El concepto de lo estadísticamente significativo es de hecho muy simple, pero tiene un nombre un poco desafortunado. Si los datos nos permiten rechazar la hipótesis nula, decimos que “el resultado es estadísticamente significativo, lo que muchas veces se reduce a”el resultado es significativo“. Esta terminología es un poco antigua, y data de la época cuando”lo significativo" significaba más bien algo como “lo indicado”, y no el significado moderno que lo acerca más a “lo importante” (particularmente en inglés). Como resultado, muchos estudiantes de nuestra época se confundirán al aprender estadística, ya que pensarán que un “resultado significativo” tiene que ser un resultado importante, cuando no necesariamente es así. Lo que “estadísticamente significativo” quiere decir es que los datos le permiten rechazar la hipótesis nula. Si el resultado es importante o no en el mundo real es una pregunta muy distinta, que depende de muchas otras cosas.

3.4.3 La diferencia entre los test de contraste de hipótesis unilateral y bilateral

Falta señalar un aspecto sobre el contraste de hipótesis que hemos construido. Si paramos un momento para pensar en las hipótesis estadísticas que estamos utilizando,

\[ \begin{array}{cc} H_0 : & \theta = .5 \\ H_1 : & \theta \neq .5 \end{array} \]

veremos que la hipótesis alternativa cubre dos posibilidades: la posibilidad de que $\theta < .5$ y la posibilidad de que $\theta > .5$. Esto tiene sentido si creemos que la PES puede producir un resultado mejor que el azar o peor que el azar. En lenguaje estadístico, esto es un ejemplo de un test bilateral o a dos colas. Recibe este nombre que la hipótesis alternativa cubre el área a ambos lados de la hipótesis nula, y como consecuencia su región crítica cubrirá ambas colas de la distribución muestral (2.5% a cada lado si $\alpha =.05$), tal y como vemos en la Figura 3.2.

Sin embargo, esta no es la única posibilidad. Podría darse el caso, por ejemplo, que sólo esté dispuesto a creer en la PES si produce resultados mejor que el azar. Así, mi hipótesis alternativa solo cubrirá la posibilidad de que $\theta > .5$, y en consecuencia la hipótesis nula de convierte en $\theta \leq .5$:

\[ \begin{array}{cc} H_0 : & \theta \leq .5 \\ H_1 : & \theta > .5 \end{array} \]

Cuando esto sucede, estamos ante un test unilateral o de una cola, el cual cubre únicamente una cola de la distribución muestral. Esto se ilustra en la Figura 3.3.

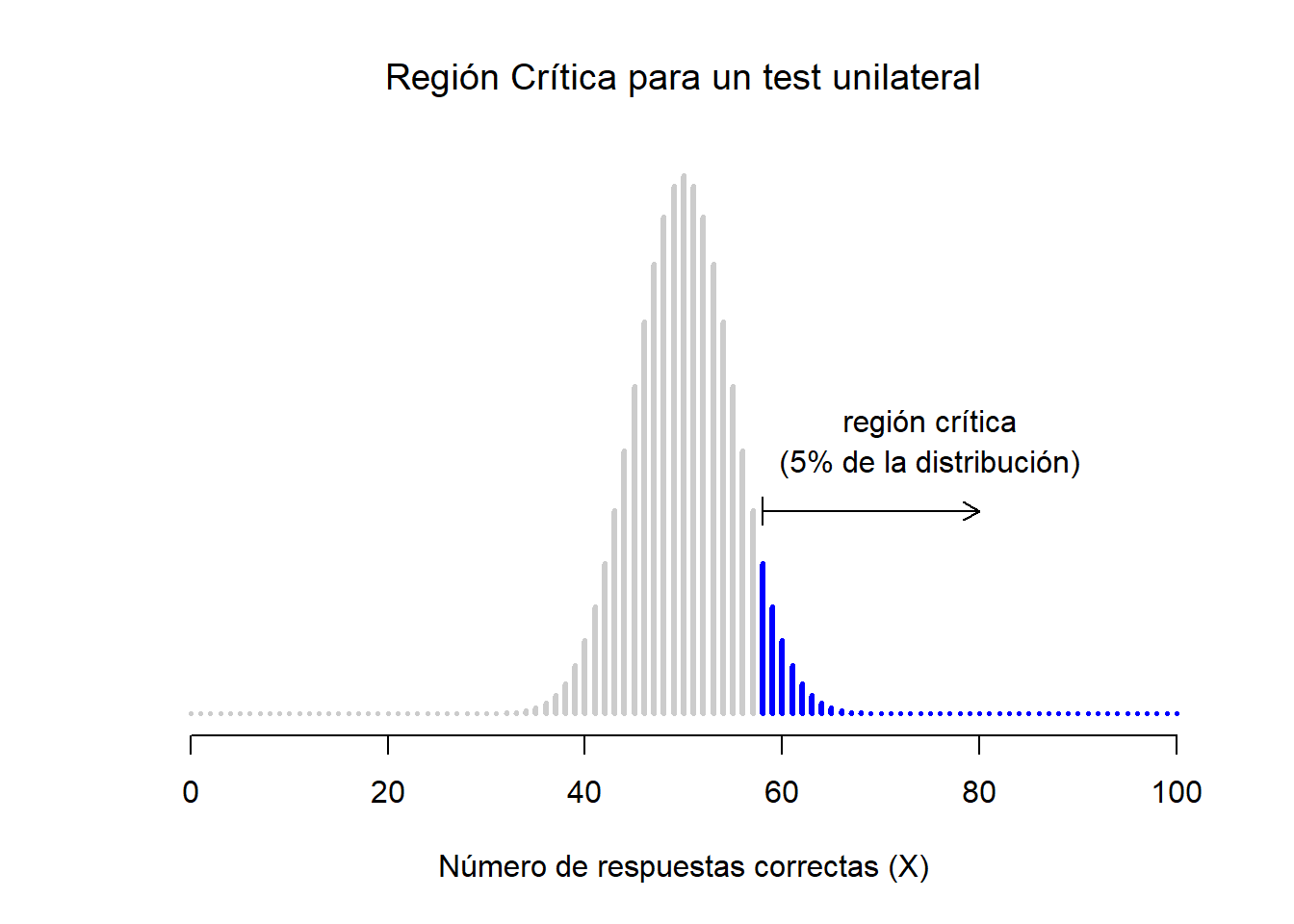
$La región crítica para un test unilateral o de una cola. En este caso, la hipótesis alternativa es que $\theta > .05$, por lo que sólo rechazaríamos la hipótesis nula en caso de tener valores altos de $X$. Como resultado, la región crítica sólo cubre la cola superior de la distribución muestral, concretamente el 5% más alto de la distribución.$

Figure 3.3: La región crítica para un test unilateral o de una cola. En este caso, la hipótesis alternativa es que $\theta > .05$, por lo que sólo rechazaríamos la hipótesis nula en caso de tener valores altos de $X$. Como resultado, la región crítica sólo cubre la cola superior de la distribución muestral, concretamente el 5% más alto de la distribución.

Nota. La descripción que verás a continuación difiere un poco de lo que podrías encontrar en un libro de introducción a la estadística tradicional. La teoría ortodoxa sobre el contraste de hipótesis surgió del trabajo de Sir Ronald Fischer y Jerzy Neyman a principios del siglo XX; sin embargo, Fischer y Neyman tenían visiones muy diferentes sobre como debería funcionar. Normalmente, los libros de texto utilizan una método que mezcla ambas aproximaciones. Aquí nos inclinaremos un poco más por la vía de Neyman, especialmente en relación al significado del valor $p$.↩︎
Si no sabes lo que es, te dejo este vídeo.(https://www.cc.com/video/bhf8jv/the-colbert-report-time-traveling-porn-daryl-bem)↩︎
Una nota sobre el lenguaje que se utiliza en el contraste de hipótesis. En general, deberás evitar utilizar la palabra demostrar: un test estadístico en realidad no prueba que una hipótesis sea verdadera o falsa. Probar implica certeza, y, como hemos visto, en estadística nada es certero. En esto, la mayoría está de acuerdo. Sin embargo, a partir de aquí hay confusión en el uso de los términos. Algunos argumentan que solo puedes utilizar frases como “rechazo la hipótesis nula”, “fallo en rechazar la hipótesis nula” o posiblemente “mantengo la hipótesis nula”. De acuerdo con esta línea de pensamiento, no puedes decir cosas como “acepto la hipótesis alternativa” o “acepto la hipótesis nula”. Esto es más debatible: aquí se mezclan ideas y conceptos sobre la hipótesis nula y el falsacionismo de Karl Popper. Aunque hay similitudes, no son exactamente iguales. Yo pienso que es correcto sobre sobre aceptar una hipótesis (bajo la premisa que aceptar no significa que sea verdad, especialmente en el caso de la hipótesis nula), aunque otros no estarán de acuerdo.↩︎
Estrictamente hablando, este test tiene un valor alfa $\alpha = .057$, lo cual es bastante generoso. Sin embargo, si hubiese escogido 39 y 61 como los límites de la región crítica, esta sólo cubriría un 3.5% de la distribución. Creo que tiene más sentido, para este ejemplo, dejar 40 y 60 como los valores críticos, con el inconveniente de tener que tolerar un error de tipo I del 5.7%, que es lo que nos deja más cerca del valor de $\alpha = .05$.↩︎

	retener \(H_0\)	rechazar \(H_0\)
\(H_0\) es verdadera	\(1-\alpha\) (probabilidad de retener correctamente)	\(\alpha\) (error de tipo I)
\(H_0\) es falsa	\(\beta\) (error de tipo II)	\(1-\beta\) (poder del test)