Capítulo 8 Barcos de papel
Figura 8.1: La boa ingiriendo un elefante
Enseñé mi obra maestra a los mayores y les pregunté si les daba miedo. Me contestaron: -¿Por qué me iba a dar miedo un sombrero? Mi dibujo no representaba un sombrero. Representaba una serpiente boa que digería un elefante. Dibujé entonces el interior de la serpiente boa para que los mayores pudiesen entender.—El Principito de Saint-Exupéry (1900-1944).
Todos hemos visto la figura de la distribución normal, esa que parece una campana, muchos le nombran campana de Gauss; no obstante, pocos investigadores saben lo que hay dentro de ella. Al igual que El Principito, quien dibuja el interior de la boa para que todos se den cuenta de que la figura no es un sombrero, sino una boa que está digiriendo un elefante; debemos hacer visible el interior de esa campana para que todos descubran que no es una campana, sino que en su interior se encuentran las medias de muchas muestras del mismo tamaño; estas medias se agrupan y amontonan dándole esa forma característica. Los estadísticos suelen referirse a este fenómeno con el nombre de distribución probabilística. Es decir, las medias de estas muestras se distribuyen según su probabilidad. ¿Probabilidad de qué?, sigue conmigo para averiguarlo.
¿Alguna vez has hecho barcos de papel? ¿Recuerdas que descubriste instintivamente que el primer barco lo podías hacer más chico doblándolo nuevamente? El barco frecuencias absolutas lo puedes dividir entre los sujetos para hacer un barco más pequeño, pero más robusto llamado frecuencias relativas (i.e. porcentajes). El barco que suma varias observaciones: calificaciones, evaluaciones, etc. también se hace más pequeño al dividirlo entre los casos o sujetos para convertirlo en el barco de la media; más descriptiva y con mayor significado que la suma de esas observaciones. Incluso puedes doblar el barco de la suma de las desviaciones al cuadrado para obtener el poderoso barco de la varianza y desdoblar esa varianza para convertirla en desviación estándar. ¡Ah!, pero el Perla Negra de Jack Sparrow, el barco que te va a sacar de cualquier apuro, no se hace con una simple muestra, sino con muchas. A razón de que está hecho de muestras y no de casos, la desviación es más pequeña que la de una desviación estándar; en estadística ese otro tipo de desviación se conoce como error estándar. La desviación y error estándar son parecidos, ambos describen la desviación, pero el primero mide la distancia promedio de los sujetos o casos a la media muestral, mientras que el segundo mide la distancia promedio que hay de las medias muestrales a la media verdadera; la media verdadera es la de toda la población, no la de una muestra. En lugar de utilizar observaciones individuales se emplean las medias de múltiples muestras, todas del mismo tamaño, como si fueran casos o sujetos para calcular la desviación estándar, que en este caso se llama error estándar. Es difícil imaginarse cómo es que se obtienen muchas muestras para calcular estos nuevos instrumentos de medición y cuál es su utilidad; sigue leyendo para satisfacer tu curiosidad.
¿Qué observaron los grandes genios de la estadística? Piensa en el relato de Tucídides, ¿crees que, si los griegos hubiesen mandado a tres grupos de soldados, digamos de cinco soldados cada uno, a contar las filas de la muralla, la media de filas de esos grupos sería la misma? Podría ser, pero es poco probable. Tiene que haber variación, unas veces es mucha y otras veces es poca, pero siempre la hay cuando se mide varias veces. Técnicamente la media de cualquier muestra es un error porque no es igual a la media verdadera. Y aunque fuera idéntica, no hay posibilidad de saberlo; por eso se hace en primera instancia cualquier estudio, porque se necesita estimarla. Lo cool de este tema es que ese valor real se puede inferir con cierta probabilidad. La naturaleza mostró a las personas como Gauss que si hacen varias muestras de buen tamaño14 y calculan sus medias, éstas se acercan a la media verdadera. ¿Qué tan cerca están de ella? Tanto que más de la mitad, exactamente el \(68\%\), se distribuyen de forma proporcional hacia la izquierda y hacia la derecha del valor real, porque la media muestral puede estar por debajo o por arriba de la media poblacional. De la misma forma, otro porcentaje de medias muestrales se encuentra al doble de la distancia que ese primer \(68\%\), juntos suman el \(95\%\) de todas las medias; el \(99\%\) de todas las medias se encuentran a no más del triple de distancia de la media verdadera y, finalmente, sólo un \(1\%\) está a más del triple de esa distancia. En otras palabras, el \(50\%\) de las medias muestrales se encuentran a la izquierda de la media poblacional y el otro \(50\%\) a la derecha, pero como hay menos casos conforme el error es más grande, se forma una especie de campana que suena cuando los errores son muy grandes; el error es lo que hace que suene la campana de Gauss.
En la tabla 8.1 tenemos tres supuestos grupos de cinco soldados cada uno y el número de filas de bloques de la muralla que contó cada uno de ellos. El primer soldado del grupo 1 contó \(113\) filas, el soldado 1 del grupo 2 llegó con un reporte de \(88\) filas; mientras que el primer soldado del grupo 3 alcanzó a contar \(93\) filas. ¿Cómo es posible que sean tan variadas estas cuentas si se trata del mismo muro? La respuesta está en que cualquier tipo de mediciones contiene un error, no son exactas, mucho menos si las hace un humano. Las respuestas no son únicamente diferentes entre grupos también los son intragrupo. Por ejemplo, en el grupo 1 el soldado 2 contó \(137\) filas, \(64\) más que el soldado 5, quien contó \(73\) filas. La media de cada grupo está cercana al valor verdadero de filas del muro que es \(100\) (por favor, piensa que esa era la altura real del muro); el grupo 1 promedia \(107.8\) filas, el grupo 2 \(95.6\) filas, en tanto que el grupo 3 tiene un promedio de \(111.4\) filas, pero ninguno de ellos es preciso. Darse cuenta de que una media de una muestra es muy parecida a la media real es en sí mismo un hallazgo, pero notar en qué proporción se le parece, lo es aun más. El grupo 3 tiene la desviación estándar más pequeña, únicamente \(14.9\) filas en promedio, pero la desviación de las medias es de tan sólo \(8.2\)15. En pocas palabras, porporcionalmente no es la misma variación que hay dentro de una muestra que la que hay entre muestras; eso está claro, pero ¿cómo calcular la proporción de variación de esta última para estimar qué tan equivocada podría estar una media muestral del valor real?
| Soldados | Grupo_1 | Grupo_2 | Grupo_3 |
|---|---|---|---|
| Soldado_1 | 113.0 | 88.0 | 93.0 |
| Soldado_2 | 137.0 | 77.0 | 122.0 |
| Soldado_3 | 94.0 | 89.0 | 129.0 |
| Soldado_4 | 122.0 | 111.0 | 100.0 |
| Soldado_5 | 73.0 | 113.0 | 113.0 |
| —Suma | 539.0 | 478.0 | 557.0 |
| —Media | 107.8 | 95.6 | 111.4 |
| —Des._estándar | 24.9 | 15.7 | 14.9 |
Espero que me hayas seguido hasta aquí, porque ahora viene lo más interesante. Es ingenuo pensar que los griegos hubieran mandado a 3 grupos o más para hacer este conteo. Estaban en juego sus vidas, y probablemente no tenían los hombres ni el tiempo para hacerlo. Lo mismo pasa con la investigación de mercados, los recursos con los que cuenta son limitados y hay muchas variables que hacen inconveniente realizar múltiples estudios para calcular el error estándar16. Por fortuna, se encontró que la reducción en la variación es inversamente proporcional al tamaño de una muestra; eso es lo que dice la ecuación (8.1). Sí, esa raíz cuadrada que hay en el denominador está diciendo que el error estándar: \(SE_{\tilde{x}}\) es igual a la desviación estándar que varía en proporción inversa al tamaño de la muestra. Por ende, el error estándar es pequeño ante una muestra grande. Si cuadruplicas la muestra el error se reduce aproximadamente a la mitad. Repara en que \(SE_{\tilde{x}}\) (Standard Error) se refiere al error estándar de la media porque se estima a partir de una muestra, no de muchas. Como acabas de ver, se usa la desviación estándar de una muestra \(s\) y el tamaño de ella \(n\)17 y se aplica la fórmula que ajusta o estandariza esa desviación. El gran hallazgo fue darse cuenta de que existe una relación inversamente proporcional entre la desviación estándar de una muestra y su tamaño. Es la misma desviación que habría si se obtuviera a partir de varias muestras; no se necesita hacer varios estudios para calcularla. La siguiente pregunta debería de ser: ¿Qué gano con conocer la desviación estándar de varias muestras o, mejor dicho, el error estándar?
\[\begin{equation} SE_{\tilde{x}}=\frac{s}{\sqrt{n}} \tag{8.1} \end{equation}\]
Mira la figura 8.2, hay \(29\) muestras de un total de \(100\) que tienen una media entre \(101\) y \(105\) filas de altura del muro. O sea que \(29\) grupos, cada uno de ellos de \(5\) soldados, contaron en promedio entre \(101\) y hasta \(105\) filas18. Para poder comparar este resultado es necesario convertirlo en frecuencias relativas, o sea porcentajes. El cálculo es fácil porque si son \(100\) muestras \(29\) de ellas equivale al \(29\%\). ¿Cuántos grupos contaron entre \(81\) y \(85\) filas de altura y entre \(121\) y \(125\) filas?, \(3\) o \(3\%\). Se puede ver en los extremos de la gráfica. La primera anotación, y quizá la más importante, es que la figura tiene una forma de campana: alta en medio, donde está el valor real de la media, \(100\) filas de altura. Y muy baja a los lados, donde es muy difícil que se encuentre el valor real de la media. Dicho de otra forma, son más probables los resultados más cercanos a la media que los más lejanos a ella. La segunda anotación es que el \(95\%\) de los valores se encuentran entre dos desviaciones a la izquierda de la media y dos a la derecha de ella. El \(95\%\) de las medias deben estar entre…, mejor veámoslo. La desviación estándar de \(100\) grupos de \(5\%\) soldados cada uno es \(7.7\). Si usamos la ecuación (8.1) y los datos de desviación estándar de la tabla 8.1 para estimar el error estándar del primer grupo de soldados, el resultado sería: \(\frac{24.9}{\sqrt{5}}=11.13\); claramente no es el valor real de la desviación promedio. ¿Qué tal si usamos la segunda muestra: \(\frac{15.7}{\sqrt{5}}=7.02\) tampoco es; aunque se acerca mucho. ¿Qué pasa si usamos la tercera muestra de soldados?: \(\frac{14.9}{\sqrt{5}}=6.66\); no, tampoco se parece. Sin embargo, son muy exactas para calcular la distancia que hay de la media muestral a la media real. Si usamos el error estándar del grupo \(1\): \(11.13\), la media poblacional debe estar, con un \(95\%\) de certeza, entre \(85\) y \(130\) numero de filas de altura. O sea, sumando y restando dos desviaciones estándar a la media del grupo: \(107.8-(2\times11.13)=85.5\) del lado izquierdo de la gráfica y \(107.8+(2\times11.13)=130\) del lado derecho de la misma gráfica. ¿Es cierto qué la media real está entre \(85\) y \(130\)? Sí, incluso la frontera del lado derecho se extiende mucho más allá de las medias existentes; la media más alta es \(125\). ¿Qué pasa si usamos los otros dos errores estándar que calculamos? Por ejemplo, el del grupo \(3\), \(111.4-(2\times6.66)=98\) es el límite inferior y \(111.4+(2\times6.66)=124\) es el superior. Si eres observador notarás que este último resultado es apenas exacto. Eso nos lleva a una tercera consideración: las muestras pequeñas, como en este caso que son de 5 soldados, tienen una distribución un poco quisquillosa. ¿Qué tan pequeñas?, típicamente menores a 30 casos. Para esas muestras pequeñas, todavía hacía falta conocer cómo se distribuían, eso fue lo que hizo William Sealy Gosset y, como cualquier apasionado de lo que hace, aplicó la nueva distribución en su trabajo a través de su famosa t-test o t de student; tema de la siguiente sección.
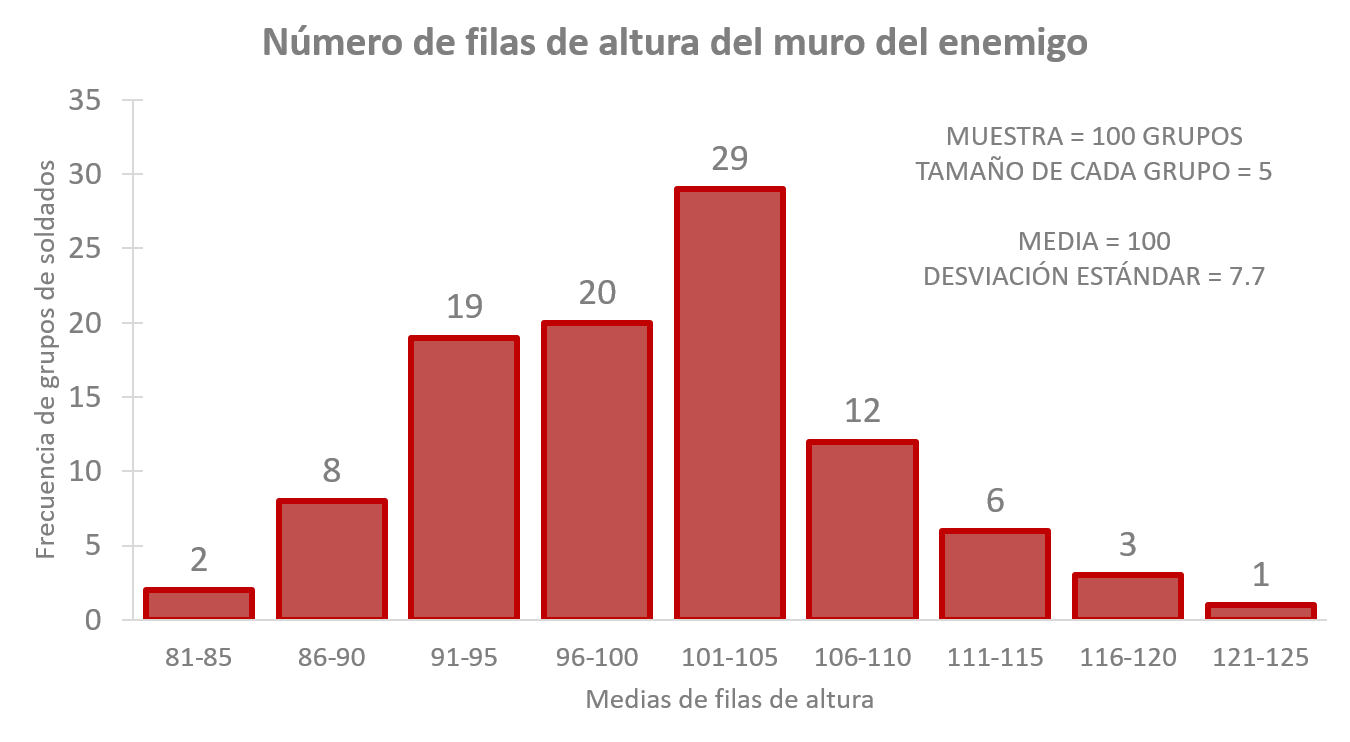
Figura 8.2: Medias de 100 muestras o grupos de 5 soldados
Retomando la pregunta sobre qué ganamos con saber que el valor (media) de una muestra de determinado tamaño tiene un 95% de probabilidad de estar entre dos errores estándar a la izquierda y dos a la derecha del valor real (media poblacional), la respuesta es ahora muy clara: cualquier resultado de una investigación se puede asegurar utilizando límites inferiores y superiores de lo que podría ser el parámetro verdadero; así se dice cuando se habla de la media poblacional. Fíjate en esta imagen usual: Si hoy fueran las elecciones, el \(42\%\) votaría por Juanito. Si usas el error estándar para calcular dentro de qué rango caen el \(95\%\) de los resultados (imagina que el error estándar es de \(2.5\%\)) la frase podría ser algo cómo: En el peor de los casos el \(37\%\) votará por Juanito y en el mejor de ellos lo hará el \(47\%\). ¿Te diste cuenta qué hicimos? Para construir un intervalo dentro del cual sabemos que está el valor verdadero, únicamente restamos dos errores estándar al resultado de la muestra: \(42\%-5\%=37\%\) y le sumamos dos: \(42\%+5\%=47\%\). De acuerdo con la teoría de la probabilidad, el \(95\%\) de todas las muestras que se pudieran hacer van a estar dentro de ese intervalo de resultados. Práctico, ¡¿verdad?! Lo que acabas de aprender es la base sobre la cual se construyen casi todas las pruebas de inferencia estadística: \(t-test\), \(Anova\), \(Chi\) \(Cuadrado\), etc. Vamos a ver algunas de éstas, pero antes un botón de muestra del uso del error estándar.
El principal sustento de la distribución normal es el tamaño de la muestra; cualquier muestra, sin importar cuál sea la distribución de la que parte (normal, uniforme, binomial, poisson, etc.) lo suficientemente grande, aproximadamente arriba de 30 casos, tiene una distribución normal. Los científicos se refieren a este fenómeno como Teorema del Límite Central.↩
La media de medias es \(104.9\): \(\frac{107.8+95.6+111.4}{3}=104.93\). La suma de cuadrados es \(134.75\): \((107.8-104.9)^2+(95.6-104.9)^2+(111.4-104.9)^2=134.75\). La varianza sería \(67.375\): \(\frac{134.75}{2}=67.375\); se divide entre 2 por los famosos grados de libertad: \(3-1=2\). Para obtener la desviación estándar extraemos su raíz cuadrada: \(\sqrt{67.375}=8.20\). Este numerito es el error estándar porque se derivo de medias muestrales y no de casos. No hicimos nada que no te hayamos explicado con anterioridad.↩
En la investigación de mercados, o social, existen los estudios llamados continuos, longitudinales, mejor conocidos como trackers o tracking; esos repiten los experimentos con el fin de medir variaciones debidas a variables que cambian a través del tiempo (v.gr., inversión publicitaria, cambio en la formulación de productos, etc.); el objetivo de esos estudios es distinto a obtener un indicador preciso de un evento en particular.↩
No te preguntas por qué este denominador, o más bien por qué la desviación estándar, \(s\), no se divide por \(n-1\); ¿no es acaso, así como se calculan las desviaciones? No hay necesidad, ya existe la desviación; es decir, la estimación ya está hecha de tal forma que los grados de libertad son totales; no se necesita ajustar las variables independientes (las que dividen).↩
Los resultados se agrupan en rangos: \(96\) a \(100\), \(101\) a \(105\), \(106\) a \(110\), etc., eso es lo que da densidad a las barras de la gráfica y permite observar una figura parecida a una campana.↩