Chapter 7 Assignment 7 - Wage Analytics – Predicting High vs Low Earners Using Logistic Regression

7.1 Introduction

The Wage Analytics Division (WAD) has hired me as their new Data Scientist. My assignment is to determine whether demographic and employment characteristics can be used to predict whether a worker earns a high or low wage.

Using the Wage dataset from the ISLR package, I will create a binary wage category, explore statistical relationships between variables, and build a logistic regression model capable of predicting wage level using demographic, job, and health-related information.

My analysis will help the company understand which characteristics are associated with higher earnings and evaluate how well a predictive model performs on unseen data.

library(ISLR)
library(tidyverse)
library(ggthemes)
library(skimr)
library(caret)
library(pROC)
library(mosaic)
library(pscl)
library(car)
library(supernova)
library(lsr)
library(caTools)
library(knitr)

7.2 Step 1 – Create the WageCategory Variable

data(Wage)
Wage %>% head(n=5) %>% kable(caption = "Wage Dataset (first 5 rows)")
(#tab:load and WageCategory)Wage Dataset (first 5 rows)
year age maritl race education region jobclass health health_ins logwage wage
231655 2006 18 1. Never Married 1. White 1. < HS Grad 2. Middle Atlantic 1. Industrial 1. <=Good 2. No 4.318063 75.04315
86582 2004 24 1. Never Married 1. White 4. College Grad 2. Middle Atlantic 2. Information 2. >=Very Good 2. No 4.255273 70.47602
161300 2003 45 2. Married 1. White 3. Some College 2. Middle Atlantic 1. Industrial 1. <=Good 1. Yes 4.875061 130.98218
155159 2003 43 2. Married 3. Asian 4. College Grad 2. Middle Atlantic 2. Information 2. >=Very Good 1. Yes 5.041393 154.68529
11443 2005 50 4. Divorced 1. White 2. HS Grad 2. Middle Atlantic 2. Information 1. <=Good 1. Yes 4.318063 75.04315 
median_wage<- median(Wage$wage)

Wage <- Wage %>% mutate(
    WageCategory = case_when(
      wage > median_wage ~ "High",
      wage <= median_wage ~ "Low"),
    WageCategory = as.factor(WageCategory)
  )

Wage %>% head(n=5) %>% kable(caption = "Wage Dataset Including Wage Category (first 5 rows)")
(#tab:load and WageCategory)Wage Dataset Including Wage Category (first 5 rows)
year age maritl race education region jobclass health health_ins logwage wage WageCategory
231655 2006 18 1. Never Married 1. White 1. < HS Grad 2. Middle Atlantic 1. Industrial 1. <=Good 2. No 4.318063 75.04315 Low
86582 2004 24 1. Never Married 1. White 4. College Grad 2. Middle Atlantic 2. Information 2. >=Very Good 2. No 4.255273 70.47602 Low
161300 2003 45 2. Married 1. White 3. Some College 2. Middle Atlantic 1. Industrial 1. <=Good 1. Yes 4.875061 130.98218 High
155159 2003 43 2. Married 3. Asian 4. College Grad 2. Middle Atlantic 2. Information 2. >=Very Good 1. Yes 5.041393 154.68529 High
11443 2005 50 4. Divorced 1. White 2. HS Grad 2. Middle Atlantic 2. Information 1. <=Good 1. Yes 4.318063 75.04315 Low

7.3 Step 2 – Data Cleaning

colnames(Wage)
##  [1] "year"         "age"          "maritl"       "race"         "education"   
##  [6] "region"       "jobclass"     "health"       "health_ins"   "logwage"     
## [11] "wage"         "WageCategory"
Wage <- Wage %>%
  mutate(
    across(
      c("maritl", "race", "education", "region", "jobclass", "health", "health_ins"), 
      ~substring(.x, 4)
    )
  )

Wage %>% head(n=5) %>% kable(caption = "Cleaned Wage Dataset (first 5 rows)")
Table 7.1: Cleaned Wage Dataset (first 5 rows)
year age maritl race education region jobclass health health_ins logwage wage WageCategory
231655 2006 18 Never Married White < HS Grad Middle Atlantic Industrial <=Good No 4.318063 75.04315 Low
86582 2004 24 Never Married White College Grad Middle Atlantic Information >=Very Good No 4.255273 70.47602 Low
161300 2003 45 Married White Some College Middle Atlantic Industrial <=Good Yes 4.875061 130.98218 High
155159 2003 43 Married Asian College Grad Middle Atlantic Information >=Very Good Yes 5.041393 154.68529 High
11443 2005 50 Divorced White HS Grad Middle Atlantic Information <=Good Yes 4.318063 75.04315 Low

7.4 Step 3 – Classical Statistical Tests

7.4.1 A) T-Test

t.test(age ~ WageCategory, data = Wage)
## 
##  Welch Two Sample t-test
## 
## data:  age by WageCategory
## t = 10.888, df = 2855, p-value < 2.2e-16
## alternative hypothesis: true difference in means between group High and group Low is not equal to 0
## 95 percent confidence interval:
##  3.681416 5.298535
## sample estimates:
## mean in group High  mean in group Low 
##           44.68510           40.19512

  • Mean age for high earners: 45 years old

  • Mean age for low earners: 40 years old

  • t-statistic: 10.9

  • df: 2855

  • p-value < 2.2e-16

Age seems to differ between high earners and low earners. We have a high t-statistic and a very small p-value, suggesting that we are very confident in a large difference between the ages in both wage categories.

7.4.2 B) ANOVA

favstats(wage ~ education, data = Wage) %>% arrange(desc(mean)) %>% kable()
education min Q1 median Q3 max mean sd n missing
Advanced Degree 38.60591 117.14682 141.77517 171.49763 318.3424 150.91778 53.90421 426 0
College Grad 32.36641 99.68946 118.88436 143.13494 281.7460 124.42791 41.18907 685 0
Some College 20.08554 89.24288 104.92151 121.38842 314.3293 107.75557 32.47473 650 0
HS Grad 23.27470 77.94638 94.07271 109.83399 318.3424 95.78335 28.56756 971 0
< HS Grad 20.93438 70.26177 81.28325 97.49329 152.2168 84.10441 21.57805 268 0 
fig.cap = "This table shows preliminary descriptive statistics such as averages and frequencies so that we can better understand our dataset and what patterns to explore regarding wage and education."
anova_model_ed<- aov(wage ~ education, data = Wage)
summary(anova_model_ed)
##               Df  Sum Sq Mean Sq F value Pr(>F)    
## education      4 1226364  306591   229.8 <2e-16 ***
## Residuals   2995 3995721    1334                   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
supernova(anova_model_ed)
##  Analysis of Variance Table (Type III SS)
##  Model: wage ~ education
## 
##                                   SS   df         MS       F   PRE     p
##  ----- --------------- | ----------- ---- ---------- ------- ----- -----
##  Model (error reduced) | 1226364.485    4 306591.121 229.806 .2348 .0000
##  Error (from model)    | 3995721.285 2995   1334.131                    
##  ----- --------------- | ----------- ---- ---------- ------- ----- -----
##  Total (empty model)   | 5222085.770 2999   1741.276

  • F-statistic: 229.81

  • df: 2999

  • p-value < 2e-16

With a very large F-statistic and a very small p-value, we can conclude that the variation in wages between education levels is statistically significant. Also, our PRE tells us that education level accounts for 23% of variance in wages.

7.4.3 C) Chi-Square/Association Test

cont_table<- table(Wage$race, Wage$WageCategory)
cont_table %>% kable()
High Low
Asian 113 77
Black 102 191
Other 9 28
White 1259 1221 
fig.cap = "This figure is a contingency table representing the number of people in each wage category grouped by race."

Wage$race<- as.factor(Wage$race)
str(Wage$race)
##  Factor w/ 4 levels "Asian","Black",..: 4 4 4 1 4 4 3 1 2 4 ...
associationTest(~ WageCategory + race, data = Wage)
## 
##      Chi-square test of categorical association
## 
## Variables:   WageCategory, race 
## 
## Hypotheses: 
##    null:        variables are independent of one another
##    alternative: some contingency exists between variables
## 
## Observed contingency table:
##             race
## WageCategory Asian Black Other White
##         High   113   102     9  1259
##         Low     77   191    28  1221
## 
## Expected contingency table under the null hypothesis:
##             race
## WageCategory Asian Black Other White
##         High  93.9   145  18.3  1226
##         Low   96.1   148  18.7  1254
## 
## Test results: 
##    X-squared statistic:  43.814 
##    degrees of freedom:  3 
##    p-value:  <.001 
## 
## Other information: 
##    estimated effect size (Cramer's v):  0.121

  • χ²: 43.8

  • df: 3

  • p-value < 0.001

  • Cramer’s V: 0.121

When comparing our observed and expected values, we see that White people performed as expected. A slightly higher number of Asian people earned higher wages than expected, and a slightly higher number of Black people earned lower wages than expected. Additionally, those who marked their race as “Other” tended to earn less than expected.

With a large chi-squared value and a small p-value, we can conclude that the relationship between race and wage category is statistically significant. However, with such a small effect size, the relationship is weak and we cannot assume that race itself plays much of a role in determining wage category.

7.5 Step 4 – Logistic Regression Model

7.5.1 Predictive Model

set.seed(42)
sample <- sample.split(Wage$WageCategory, SplitRatio = 0.7)
training_data <- subset(Wage, sample == TRUE)
test_data <- subset(Wage, sample == FALSE)

7.5.2 Model Specification

train_model <- glm(WageCategory ~ age + maritl + race + education + jobclass +                       health + health_ins,
                   family = "binomial", data = training_data)

7.5.3 Logistic Regression Output

summary(train_model)
## 
## Call:
## glm(formula = WageCategory ~ age + maritl + race + education + 
##     jobclass + health + health_ins, family = "binomial", data = training_data)
## 
## Coefficients:
##                           Estimate Std. Error z value Pr(>|z|)    
## (Intercept)               3.969497   0.449412   8.833  < 2e-16 ***
## age                      -0.019159   0.005179  -3.699 0.000216 ***
## maritlMarried            -0.880983   0.198852  -4.430 9.41e-06 ***
## maritlNever Married       0.382638   0.235167   1.627 0.103718    
## maritlSeparated          -0.493750   0.445580  -1.108 0.267815    
## maritlWidowed            -0.702502   0.641162  -1.096 0.273224    
## raceBlack                 0.308966   0.280923   1.100 0.271407    
## raceOther                 0.024598   0.587975   0.042 0.966630    
## raceWhite                -0.163411   0.226615  -0.721 0.470850    
## educationAdvanced Degree -2.727178   0.262521 -10.388  < 2e-16 ***
## educationCollege Grad    -1.918224   0.229754  -8.349  < 2e-16 ***
## educationHS Grad         -0.537104   0.218967  -2.453 0.014171 *  
## educationSome College    -1.253153   0.226653  -5.529 3.22e-08 ***
## jobclassInformation      -0.239335   0.107600  -2.224 0.026128 *  
## health>=Very Good        -0.305837   0.117671  -2.599 0.009347 ** 
## health_insYes            -1.208890   0.118014 -10.244  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 2910.9  on 2099  degrees of freedom
## Residual deviance: 2225.0  on 2084  degrees of freedom
## AIC: 2257
## 
## Number of Fisher Scoring iterations: 4

7.5.4 Odds Ratio

exp(coef(train_model))
##              (Intercept)                      age            maritlMarried 
##              52.95789941               0.98102322               0.41437526 
##      maritlNever Married          maritlSeparated            maritlWidowed 
##               1.46614683               0.61033309               0.49534462 
##                raceBlack                raceOther                raceWhite 
##               1.36201634               1.02490299               0.84924198 
## educationAdvanced Degree    educationCollege Grad         educationHS Grad 
##               0.06540362               0.14686760               0.58443835 
##    educationSome College      jobclassInformation        health>=Very Good 
##               0.28560285               0.78715143               0.73650656 
##            health_insYes 
##               0.29852856

The predictors that matter most in predicting wage category is age, marital status, education, and health insurance status. Specifically, being older, married, having some college experience, a college degree, or an advanced degree, and having health insurance makes someone much less likely to earn a lower wage. Because of the fact that my model considers the positive outcome to be “Low” wage, all of these specific factors have a negative relationship with wage category (meaning they are more likely to earn a higher wage).

Having an advanced degree had the strongest effect on predicting higher wage, followed by having a college degree, then some college experience, then having active health insurance, being married, and finally older age with the smallest (but still statistically significant) effect size.

Health insurance status surprised me the most - not that it is shocking that people with higher wages tend to have health insurance, but it seems like (in my experience) many lower wage jobs still offer some sort of health insurance, If anything, I thought that it would have been a very weak predictor compared to the other variables.

7.6 Step 5 – Model Evaluation on Test Data

pR2(train_model)["McFadden"]
## fitting null model for pseudo-r2
##  McFadden 
## 0.2356458

This score tells us that our model has a good fit.

varImp(train_model) %>% arrange(desc(Overall))
##                              Overall
## educationAdvanced Degree 10.38841873
## health_insYes            10.24365057
## educationCollege Grad     8.34903942
## educationSome College     5.52894400
## maritlMarried             4.43035351
## age                       3.69944093
## health>=Very Good         2.59909015
## educationHS Grad          2.45290419
## jobclassInformation       2.22430943
## maritlNever Married       1.62708918
## maritlSeparated           1.10810734
## raceBlack                 1.09982714
## maritlWidowed             1.09566872
## raceWhite                 0.72109599
## raceOther                 0.04183507

Education (namely College Grad & Advanced Degree) and health insurance are the strongest predictors of having a higher wage.

vif(train_model)
##                GVIF Df GVIF^(1/(2*Df))
## age        1.226363  1        1.107413
## maritl     1.230025  4        1.026217
## race       1.088403  3        1.014219
## education  1.171092  4        1.019938
## jobclass   1.076950  1        1.037762
## health     1.057935  1        1.028560
## health_ins 1.020670  1        1.010282

Thankfully, our model shows no colinearity.

7.6.1 Predicted Probabilities & Classes

test_data$pred_prob <- predict(train_model, newdata = test_data, type = "response")
test_data$pred_class <- ifelse(test_data$pred_prob > 0.5, "Low", "High") %>% as.factor()
test_data %>% head(n=10) %>% kable(caption = "Predicted Probabilities and Classes (first 10 rows)")
(#tab:pred prob class)Predicted Probabilities and Classes (first 10 rows)
year age maritl race education region jobclass health health_ins logwage wage WageCategory pred_prob pred_class
231655 2006 18 Never Married White < HS Grad Middle Atlantic Industrial <=Good No 4.318063 75.04315 Low 0.9790380 Low
86582 2004 24 Never Married White College Grad Middle Atlantic Information >=Very Good No 4.255273 70.47602 Low 0.7799730 Low
376662 2008 54 Married White College Grad Middle Atlantic Information >=Very Good Yes 4.845098 127.11574 High 0.1440839 High
450601 2009 44 Married Other Some College Middle Atlantic Industrial >=Very Good Yes 5.133021 169.52854 High 0.3780648 High
305706 2007 34 Married White HS Grad Middle Atlantic Industrial >=Very Good No 4.397940 81.28325 Low 0.8070183 Low
160191 2003 37 Never Married Asian College Grad Middle Atlantic Industrial >=Very Good No 4.414973 82.67964 Low 0.8052107 Low
230312 2006 50 Married White Advanced Degree Middle Atlantic Information >=Very Good No 5.360552 212.84235 High 0.2132905 High
301585 2007 56 Married White College Grad Middle Atlantic Industrial <=Good Yes 4.861026 129.15669 High 0.2184157 High
158226 2003 38 Married Asian College Grad Middle Atlantic Information >=Very Good No 5.301030 200.54326 High 0.4742904 High
448410 2009 75 Married White College Grad Middle Atlantic Industrial >=Very Good Yes 4.447158 85.38394 Low 0.1251232 High 
fig.cap = "This table represents the test data (based on the original data) and our model's predictions about each person's wage category."

7.6.2 Confusion Matrix

conf_matrix <- confusionMatrix(test_data$pred_class, test_data$WageCategory, positive = "Low")
conf_matrix
## Confusion Matrix and Statistics
## 
##           Reference
## Prediction High Low
##       High  310 116
##       Low   135 339
##                                           
##                Accuracy : 0.7211          
##                  95% CI : (0.6906, 0.7502)
##     No Information Rate : 0.5056          
##     P-Value [Acc > NIR] : <2e-16          
##                                           
##                   Kappa : 0.4419          
##                                           
##  Mcnemar's Test P-Value : 0.2559          
##                                           
##             Sensitivity : 0.7451          
##             Specificity : 0.6966          
##          Pos Pred Value : 0.7152          
##          Neg Pred Value : 0.7277          
##              Prevalence : 0.5056          
##          Detection Rate : 0.3767          
##    Detection Prevalence : 0.5267          
##       Balanced Accuracy : 0.7208          
##                                           
##        'Positive' Class : Low             
##
  • Accuracy: 0.72
    • The model accurately predicted the correct wage category 72% of the time.
  • Sensitivity: 0.75
    • The model accurately predicted low wage earners 75% of the time.
  • Specificity: 0.70
    • The model accurately predicted high earners 70% of the time.
  • Balanced Accuracy: 0.72
    • Our balanced accuracy shows us that our observed data is likely pretty balanced, since the balanced accuracy rate is the same as our regular accuracy rate. When we run table(Wage$WageCategory), we can see that our data is very balanced (~1500 per category).

7.6.3 ROC Curve

roc_obj <- roc(test_data$WageCategory, test_data$pred_prob, levels = c("Low", "High"))
## Setting direction: controls > cases
plot(roc_obj, col = "darkblue", lwd = 2,
     main = "ROC Curve – Logistic Regression")

fig.cap = "A graph representing the model's sensitivity and specificity in wage category predictions."

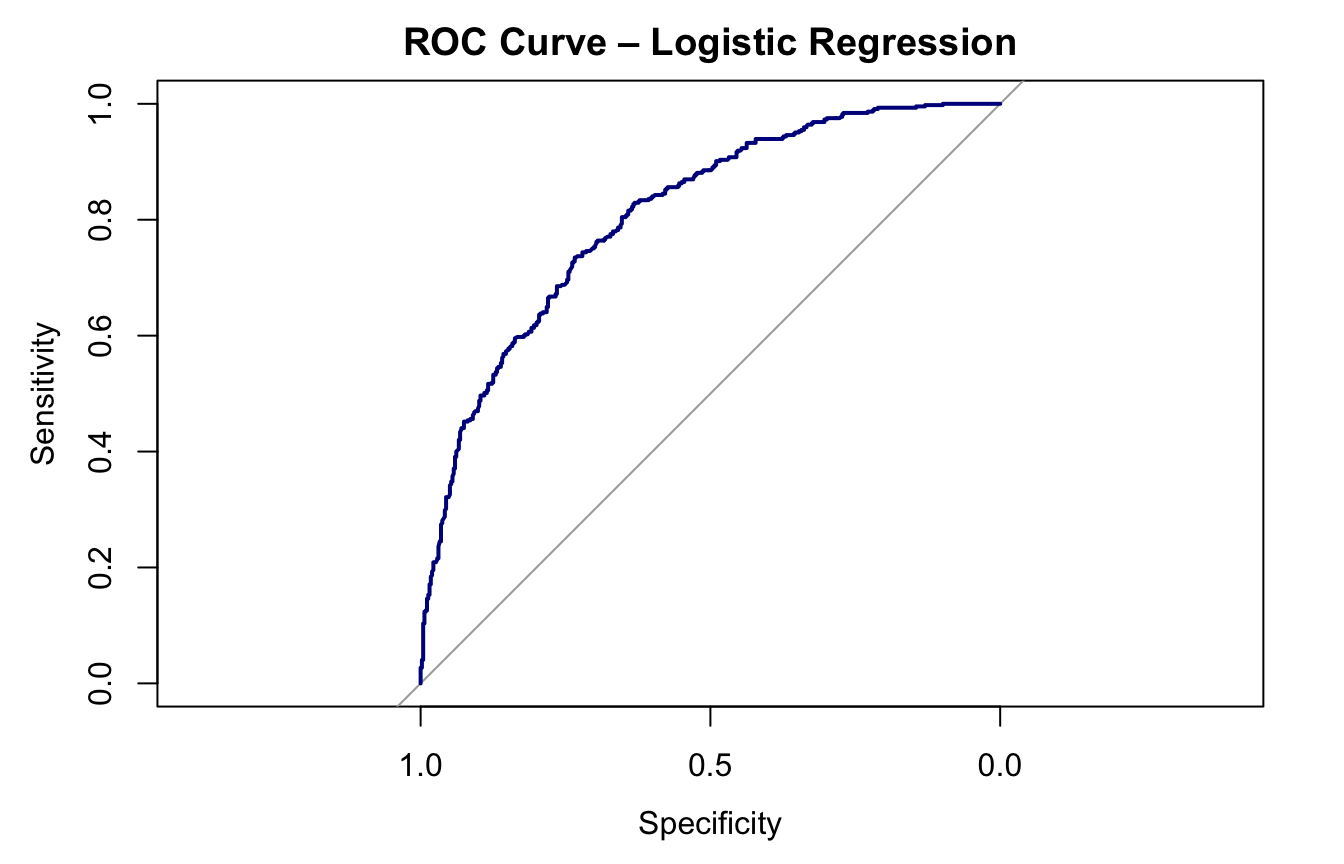
7.6.4 Area Under the Curve

auc(roc_obj)
## Area under the curve: 0.8088
ggplot(test_data, aes(x = WageCategory, y = pred_prob, fill = WageCategory)) +
  geom_boxplot(alpha = 0.7) +
  labs(title = "Predicted Probability of Wage Category",
       x = "Actual Wage Category", y = "Predicted Probability") +
  theme_minimal(base_size = 13)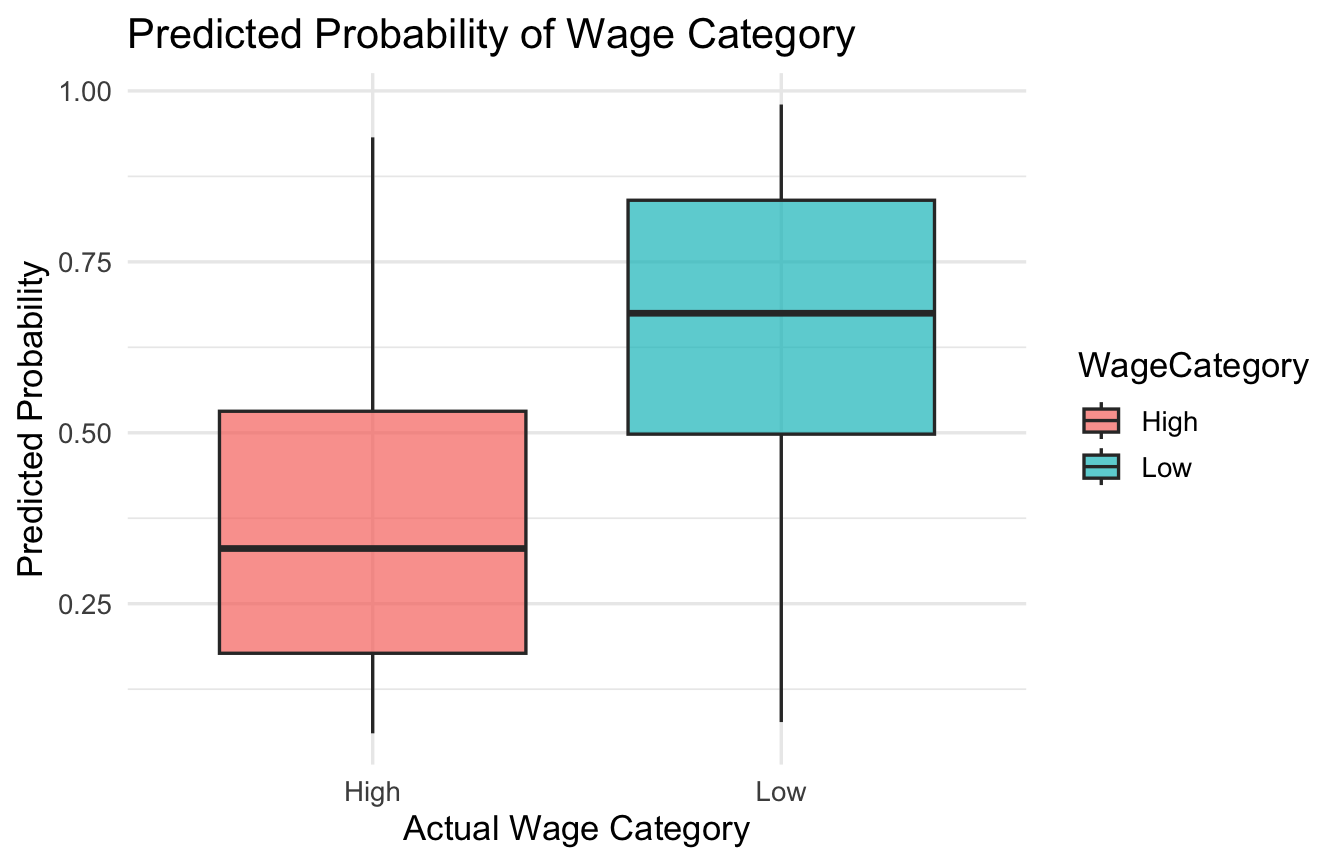

fig.cap = "A box plot representing the probability that two randomly chosen people will have their wages correctly predicted."

Our AUC is 0.81 - this tells us that our model has very strong discriminative power and can accurately separate between high wage and low wages.

The model identifies high earners at a rate of 70%, and it identifies low earners at a rate of 75%. This model performs much better than the ‘No Information Rate’ performance, which is accurate about 51% of the time (0.72 > 0.51). So, this model is definitely better at predicting outcomes than guessing.

7.7 Step 6 – Final Interpretation

Based on all of the performed analyses, multiple variables were found to have a meaningful relationship with wage category. Specifically, a t-test showed a highly significant difference in the mean age of high earners (45 years) versus low earners (40 years). The ANOVA showed that education level is a statistically significant predictor of wages, accounting for 23% of the variance. Further, a chi-squared test indicated a statistically significant but weak association between race and wage category, suggesting that other factors likely play a larger role in determining wage category. The logistic regression model was made to predict wage category (Low vs. High) and identified multiple significant predictors. The summary(train_model) output suggested that age, marital status, education level, and health insurance status were the most impactful variables. Specifically, being older, having a college or advanced degree, being married, and having health insurance were all associated with a lower likelihood of earning a low wage. The strongest predictors of a high wage were having a college or advanced degree and having health insurance, as shown by the variable importance analysis. Evaluating the model’s performance had strong results. The model had an overall accuracy of 72% and a balanced accuracy of 72%, indicating it is effective at predicting wage category for both high and low earners. This model performs significantly better than the “No Information Rate,” which was approximately 51%. The model’s discriminative power was represented by a very high AUC (Area Under the Curve) of 0.81, which suggests the model can accurately distinguish between high and low wage earners 81% of the time. The Confusion Matrix also showed that the model performed slightly better at predicting low wage earners (sensitivity of 75%) than high wage earners (specificity of 70%). If this analysis were to be repeated, I would consider adding several new variables to potentially improve the model’s predictive power. Relevant additions could include a variable of specific job types or titles (instead of a broad jobclass), and location data, as different regions may result in different wages. Given the weak relationship found in the chi-squared test and the low variable importance, I would remove race from the model to make it more parsimonious. Ideally, these additions and removals would help to capture more of the complex factors that influence wage outcomes.