Capítulo 2 Fundamentos
2.1 Variables regionalizadas
En geostatística se estudian fenómenos que se extienden en el espacio y presentan cierta organización o estructura espacial.
No se trabaja directamente con el fenómeno físico en sí, sino con su representación matemática: una variable regionalizada (o regionalización). Esta se entiende como una función numérica definida en un espacio geográfico que busca describir y medir adecuadamente dicho fenómeno.
Para comprender la idea, pensemos en un fenómeno que se distribuye en un dominio espacial \(D\).
Si realizamos mediciones en diferentes puntos del dominio, obtenemos solo una parte de la información posible, ya que en teoría podrían hacerse infinitas mediciones.
Sin embargo, por limitaciones de tiempo, costo o esfuerzo, solo se recolecta un conjunto finito de datos.
Definición 2.1 (Variable regionalizada) Cuando \(s\) recorre el dominio \(D\), el conjunto \(\{z(s), s \in D\}\) se denomina variable regionalizada o regionalización, siendo \(\{z(s_i), i=1,2,3,...\}\) una colección de valores de esa variable y cada valor individual un valor regionalizado.
Un enfoque determinista puede emplearse para describir o modelar un fenómeno regionalizado, proporcionando una estimación precisa de los valores de la regionalización. Sin embargo, este enfoque exige un conocimiento profundo del origen del fenómeno y de las leyes físicas o matemáticas que gobiernan la evolución de la variable regionalizada.
En la práctica, muchos de los fenómenos regionalizados que se estudian son tan complejos que un modelo determinista solo logra representarlos parcialmente. Por esta razón, el enfoque determinista suele ser insuficiente y se recurre al enfoque probabilístico, el cual permite no solo incorporar el conocimiento existente, sino también manejar la incertidumbre asociada al fenómeno aleatorio regionalizado.
2.2 Funciones aleatorias
Desde una perspectiva probabilística, el valor regionalizado puede interpretarse como el resultado de un mecanismo aleatorio, es decir, una variable aleatoria (va).
Si consideramos los valores regionalizados en todos los puntos de un dominio \(D\), podemos verlos como la manifestación de una función aleatoria espacial (también llamada proceso estocástico o campo aleatorio).
Definición 2.2 (Campo aleatorio espacial) Cuando \(s\) recorre el dominio bajo estudio \(D\), se tiene una familia de variables aleatorias \(\{Z(s), s \in D\}\), lo cual constituye un campo aleatorio espacial.
Esta decisión metodológica es central en la geoestadística: la variable regionalizada se interpreta como una realización de un campo aleatorio espacial.
La variable regionalizada suele ser altamente irregular en el ámbito local, lo que dificulta su representación mediante funciones deterministas, pero al mismo tiempo presenta una cierta estructura espacial u organización.
El enfoque probabilístico (o geoestadística probabilística) permite considerar ambos aspectos, el errático y el estructurado, de la siguiente manera (Emery (2000)) :
- En cada ubicación \(s\), \(Z(s)\) es una variable aleatoria (por lo que tiene un aspecto erráctico).
- Para un conjunto de puntos \(s_1, s_2, \ldots, s_k\), las variables \(Z(s_1), Z(s_2), \ldots, Z(s_k)\) están ligadas por correlaciones espaciales, responsables de la similitud en los valores (aspecto estructurado).
La geoestadística estudia tanto la irregularidad local como la estructura global de las variables regionalizadas como se aprecia en la Figura 2.1.
Code
# Paquetes
library(GeoModels)
library(fields) # para drape.plot
set.seed(199)
# Parámetros del modelo exponencial
corrmodel <- "Exponential" # nombre del modelo en GeoModels
parms <- list(mean = 0, # media
sill = 1, # varianza (sill)
nugget = 0, # nugget
scale = 0.25)
# Malla 2D (101 x 101)
step <- 0.01
x <- seq(0, 1, by = step)
y <- seq(0, 1, by = step)
# Simulación del campo gaussiano en grilla
f <- GeoSim(corrmodel = corrmodel,
param = parms,
grid = TRUE,
coordx = x, coordy = y,progress=FALSE
)$data
# Gráfico 3D
op <- par(mar = c(0,0,0,0), mgp = c(0.5,0.5,0))
drape.plot(x, y, f, col = tim.colors(), theta = 40, phi = 40)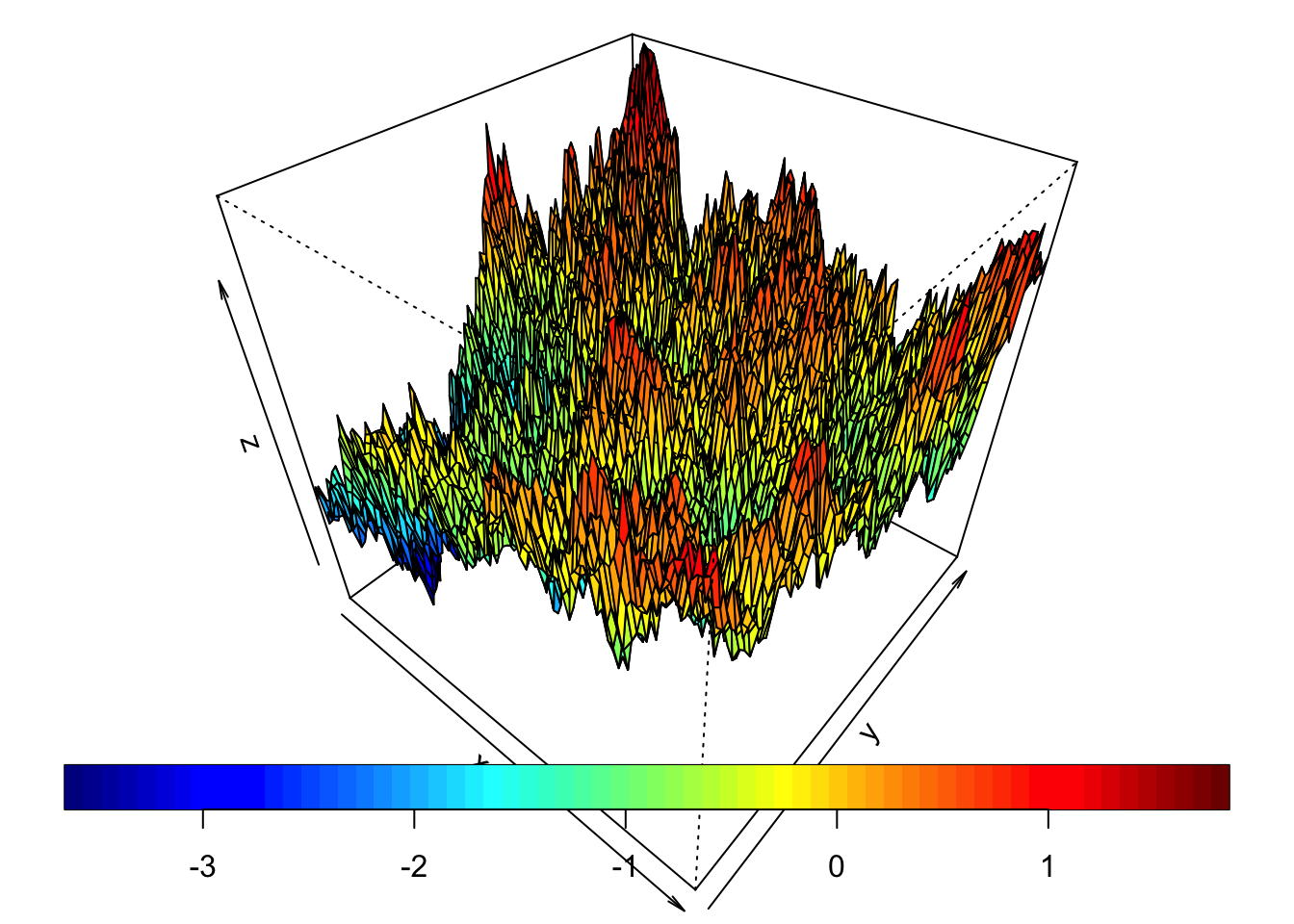
Figura 2.1: Simulación de una variable regionalizada.
Si \(Z(s)\) es un campo aleatorio y consideramos un conjunto de puntos \((s_1, \ldots, s_k)\), entonces \(Z(s)\) se caracteriza por su función de distribución conjunta k-dimensional.
El conjunto de todas estas funciones para distintos \(k\) y combinaciones posibles de puntos en el dominio se denomina ley de probabilidad espacial.
Definición 2.3 (Función de distribución conjunta k-dimensional) Dado un campo aleatorio \(Z(s)\), la función de distribución conjunta k-dimensional se define como:
\[ F(z(s_1), \ldots, z(s_k)) = P[Z(s_1) \leq z(s_1), \ldots, Z(s_k) \leq z(s_k)]. \]
En geoestadística lineal basta con conocer los dos primeros momentos de la distribución de \(Z(s)\).
En la práctica, la información disponible no suele permitir inferir momentos de orden superior.
Los momentos de interés son: media (o primer momento), varianza y covarianza (y de manera equivalente, el semivariograma).
Definición 2.4 (Esperanza o primer momento)
La esperanza de un campo aleatorio se define como una función no aleatoria de \(s\) que coincide en cada punto con el valor esperado de la variable aleatoria en ese lugar:
\[ \mu(s) = E(Z(s)), \quad \forall s \in D. \]
Cuando depende de la ubicación, también se le denomina tendencia (drift) del campo aleatorio.
Definición 2.5 (Varianza)
La varianza de un campo aleatorio se define como una función no aleatoria de \(s\) que coincide en cada punto con la varianza de la variable aleatoria en ese lugar:
\[ V(s) = V(Z(s)), \quad \forall s \in D. \]
Definición 2.6 (Covarianza)
La función de covarianza de un campo aleatorio se define como una función no aleatoria de los puntos \(s_i\) y \(s_j\), tal que para cualquier par de posiciones coincide con la covarianza entre las variables en esos puntos:
\[ C(s_i, s_j) = E\big[(Z(s_i) - \mu(s_i))(Z(s_j) - \mu(s_j))\big], \quad \forall s_i, s_j \in D. \]
Definición 2.7 (Variograma)
El variograma de un campo aleatorio se define como la varianza de las primeras diferencias:
\[ 2\gamma(s_i - s_j) = V\big(Z(s_i) - Z(s_j)\big), \quad \forall s_i, s_j \in D. \]
La función \(\gamma(s_i, s_j)\) recibe el nombre de semivariograma.
Definición 2.8 (Campo gaussiano)
Un campo aleatorio \(Z(s)\) es gaussiano si, para todo \(k\) y cualquier conjunto de puntos \(s_1, \ldots, s_k\), la distribución conjunta de \(Z(s_1), \ldots, Z(s_k)\) es una distribución gaussiana multivariante.
Una distribución gaussiana multivariante se caracteriza por un vector de medias y una matriz de varianzas-covarianzas.
Esto implica que los dos primeros momentos (media y covarianza) determinan completamente su estructura probabilística.
Por esta razón, la suposición de campos gaussianos es común en geoestadística y constituye la base de muchos métodos como el kriging.
2.3 Hipótesis de estacionariedad e hipótesis intrínseca
2.3.1 Estacionariedad
En términos probabilísticos, interpretar una variable regionalizada como la realización particular de un campo aleatorio \(\{Z(s), s \in D\}\) tiene sentido cuando es posible inferir parte (o toda) la ley de probabilidad que lo define.
En este contexto, la estacionariedad refleja un cierto grado de homogeneidad espacial en la regionalización y se considera una propiedad deseable.
En la práctica, solo disponemos de una única realización observada del campo aleatorio (la regionalización observada), lo cual sería análogo a tener un tamaño muestral de uno.
Para poder hacer inferencias válidas, se adopta la hipótesis de estacionariedad o de homogeneidad espacial, que consiste en sustituir repeticiones en el espacio por repeticiones en el tiempo o en el dominio.
En otras palabras, se asume que las observaciones en diferentes puntos del dominio tienen características equivalentes y pueden considerarse como realizaciones del mismo campo aleatorio.
Formalmente, la hipótesis de estacionariedad implica que la ley de probabilidad del campo aleatorio es invariante por traslación:
Las propiedades probabilísticas de un conjunto de observaciones no dependen de los lugares específicos donde se midieron, sino únicamente de sus separaciones.
En términos matemáticos y probabilísticos, la estacionariedad describe el comportamiento espacial regular de los momentos del campo aleatorio, o del campo mismo.
Existen distintos grados de estacionariedad, y según el supuesto adoptado, podemos tratar a las variables como si tuvieran la misma distribución o los mismos momentos, lo que permite realizar inferencias aun con información limitada.
A partir de este supuesto de homogeneidad espacial, se distinguen tres casos principales:
- Función aleatoria estrictamente estacionaria.
- Función aleatoria estacionaria de segundo orden.
- Función aleatoria intrínsecamente estacionaria (o con incrementos estacionarios).
2.3.2 Funciones aleatorias estrictamente estacionarias
Definición 2.9 (Estacionariedad estricta)
Un campo aleatorio \(\{Z(s), s \in D\}\) es estrictamente estacionario si, para todo \(k\) y para cualquier conjunto de puntos espaciales \(s_1, s_2, \ldots, s_k\), y cualquier vector de traslación \(h \in \mathbb{R}^d\), las familias de variables aleatorias
\[ Z(s_1), Z(s_2), \ldots, Z(s_k) \quad \text{y} \quad Z(s_1+h), Z(s_2+h), \ldots, Z(s_k+h) \quad \tag{2.1} \]
tienen la misma función de distribución conjunta, siempre que los puntos trasladados permanezcan dentro del dominio \(D\).
En otras palabras, la distribución conjunta de \(\{Z(s_1), Z(s_2), \ldots, Z(s_k)\}\) no se ve afectada por una traslación arbitraria \(h\).
Esto implica que las funciones de densidad de dimensión menor que \(k\) tampoco dependen de la ubicación absoluta, sino únicamente de las distancias relativas entre los puntos.
Por ejemplo, en el caso bidimensional, si consideramos los pares \(\{Z(s_1), Z(s_2)\}\), \(\{Z(s_3), Z(s_4)\}\) y \(\{Z(s_5), Z(s_6)\}\), todos tendrán la misma distribución bivariada siempre que las distancias \(|s_1-s_2| = |s_3-s_4| = |s_5-s_6|\).
En términos generales, la estacionariedad estricta es una condición muy exigente.
Por ello, en geoestadística lineal esta hipótesis suele relajarse hacia la estacionariedad de segundo orden, que limita el análisis únicamente a los dos primeros momentos del campo aleatorio (media y covarianza/variograma).
2.3.3 Funciones aleatorias estacionarias de segundo orden
Definición 2.10 (Estacionariedad de segundo orden)
Un campo aleatorio \(\{Z(s), s \in D\}\) es estacionario de segundo orden (o débilmente estacionario) si tiene momentos de segundo orden finitos (es decir, existe la covarianza) y cumple:
- La esperanza existe y es constante, por lo que no depende de la localización \(s\):
\[ E(Z(s)) = \mu(s) = \mu.\quad \tag{2.2} \]
- La covarianza existe para cada par de variables aleatorias \(Z(s)\) y \(Z(s+h)\), y depende únicamente del vector de separación \(h\), no de la posición absoluta:
\[ C(Z(s), Z(s+h)) = C(h), \quad \forall s \in D, \; h. \quad \tag{2.3} \]
Dado que \(C(h)\) solo depende de la separación, la varianza del campo aleatorio también es constante y finita:
\[ V(Z(s)) = C(0) = \sigma^2. \quad \tag{2.4} \]
Esto implica que la variable regionalizada puede interpretarse como valores que fluctúan alrededor de un valor constante (la media), con una variación uniforme en todo el dominio.
Bajo esta hipótesis, diferentes pares de puntos separados por la misma distancia tendrán la misma covarianza como se muestra en la Figura 2.2. Específicamente, La Figura 2.2 muestra la ubicación de cuatro pares de puntos (en el caso 2D). En el caso de estricta estacionariedad, \(\{Z(s_1), Z(s_2)\}\), \(\{Z(s_3), Z(s_4)\}\) y \(\{Z(s_5), Z(s_6)\}\) tienen la misma función de distribución bivariada, porque la distancia entre los pares \(\{s_1, s_2\}\), \(\{s_3, s_4\}\) y \(\{s_5, s_6\}\) es la misma.
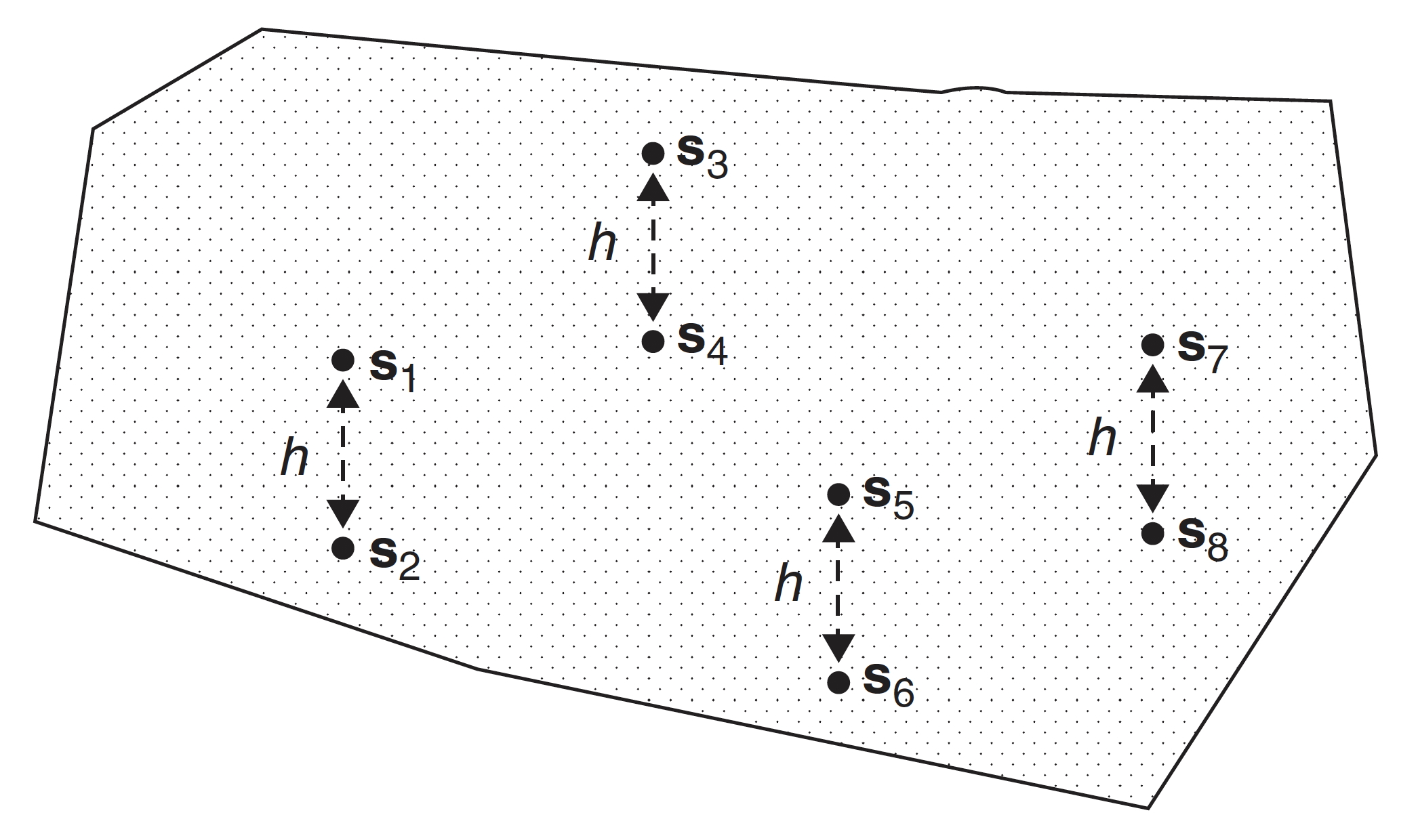
Figura 2.2: Cuatro pares de puntos separados por una distancia \(h\) en un dominio 2D.
En algunos casos, se utiliza la función de correlación espacial (o correlograma) en lugar de la covarianza:
\[ Corr(Z(s), Z(s+h)) = \frac{C(h)}{C(0)} = \rho(h). \quad \tag{2.5} \]
Además, en el caso de estacionariedad de segundo orden, la función de covarianza y el semivariograma son equivalentes para caracterizar la estructura de dependencia espacial, pues cumplen la relación:
\[ \gamma(h) = \tfrac{1}{2} V(Z(s+h) - Z(s)) = C(0) - C(h). \quad \tag{2.6} \]
Si un campo aleatorio es estrictamente estacionario, entonces también lo es en el sentido amplio (es decir, estacionario de segundo orden) como se muestra en la Figura 2.3.

Figura 2.3: Hipótesis de estacionariedad y estacionariedad intrínseca.
La recíproca, sin embargo, no siempre se cumple.
En el caso de campos aleatorios gaussianos, la estacionariedad estricta y la de segundo orden son equivalentes.
Un campo aleatorio se dice cuasi-estacionario cuando la hipótesis de estacionariedad (generalmente la de segundo orden) solo es válida para distancias \(|h| < d\), siendo \(d\) una distancia límite.
En este caso:
\[ \mu(s+h) \approx \mu(s) \quad \text{si } |h| < d, \]
y
\[ C(Z(s+h) - Z(s)) = C(h) \quad \text{si } |h| < d. \]
La estacionariedad de segundo orden también puede considerarse una hipótesis fuerte, ya que implica la existencia de la varianza del campo aleatorio.
Algunos fenómenos pueden presentar variaciones infinitas y no ser representables con una varianza finita.
En esos casos, si los incrementos o diferencias \(Z(s+h) - Z(s)\) tienen varianza finita, el campo aleatorio puede considerarse intrínsecamente estacionario.
En estas notas (salvo que se indique lo contrario), se asumirá siempre el contexto de estacionariedad de segundo orden.
2.3.4 Funciones aleatorias intrínsecamente estacionarias
Definición 2.11 (Estacionariedad intrínseca)
Un campo aleatorio \(\{Z(s), s \in D\}\) es intrínsecamente estacionario si, para cualquier vector de traslación \(h\), los incrementos de primer orden
\[ Z(s+h) - Z(s) \quad \tag{2.7} \]
son estacionarios de segundo orden, aunque el campo original no lo sea.
Esto implica que:
\[ E(Z(s+h) - Z(s)) = \mu(s), \quad \tag{2.8} \]
donde \(\mu(s)\) (la tendencia o drift) es necesariamente lineal en \(h\), y
\[ C((Z(s+h) - Z(s)), (Z(s+h+h') - Z(s+h'))) = C(h,h'), \]
lo que es equivalente a:
\[ \frac{1}{2} V(Z(s+h) - Z(s)) = \gamma(h), \quad \tag{2.9} \]
siendo \(\gamma(h)\) únicamente función de \(h\).
En el caso particular de que el drift lineal sea nulo, se cumple:
\[ E(Z(s+h) - Z(s)) = 0, \quad \; E[(Z(s+h) - Z(s))^2] = \gamma(h). \quad \tag{2.10} \]
Por lo tanto, cuando hablamos de hipótesis intrínsecas en este libro, consideraremos esta forma simplificada.
- Si un campo aleatorio es de segundo orden estacionario, entonces también es intrínsecamente estacionario.
- La recíproca no siempre es cierta. Los campos intrínsecos que no son de segundo orden se denominan estrictamente intrínsecos.
Un campo gaussiano intrínseco es aquel cuyos incrementos siguen una distribución gaussiana multivariante.
Un campo aleatorio se dice cuasi-intrínseco cuando la hipótesis intrínseca solo se cumple para distancias \(|h| < d\), donde \(d\) es una distancia límite.
2.3.4.1 Ejemplo 2.1 (Proceso de Wiener-Levy)
Consideremos el proceso discreto:
\[ Z(s_{k+1}) = Z(s_k) + \varepsilon_k, \quad \tag{2.11} \]
con \(\varepsilon_k \sim N(0,1)\) independientes, y valores en puntos univariados \(s_i, i=1,2,\ldots,k,k+1,\ldots\).
- La varianza crece indefinidamente con \(h\):
\[ V(Z(s_{k+h})) = V(Z(s_k)) + h. \quad \tag{2.12} \]
Lo anterior indica que la varianza aumenta indefinidamente cuando \(h\) crece (no es finita) y depende de \(k\) (Ver Figura 2.4).
- Si consideramos los incrementos \(Z(s_{k+h}) - Z(s_k)\):
\[ E(Z(s_{k+h}) - Z(s_k)) = 0, \quad V(Z(s_{k+h}) - Z(s_k)) = h. \quad \tag{2.13} \]
Por lo tanto:
\[ \gamma(h) = \tfrac{h}{2}. \quad \tag{2.14} \]
Code
par(mfrow = c(2, 1))
set.seed(8)
n <- 100
x <- seq(0 + 1/n, 1000, by = 1/n)
y <- cumsum(rnorm(1e+05, 0, 1))
plot(x, y, type = "l", ylab = expression(paste(Z(s[k]))), xlab = expression(paste(s[k])))
a <- diff(y)
plot(a, type = "l", ylab = expression(paste(Z(s[k + 1]) - Z(s[k]))), xlim = c(0,
1000), ylim = c(-3, 3), xlab = expression(paste(s[k])))
abline(h = 0, col = "gray80", lwd = 2)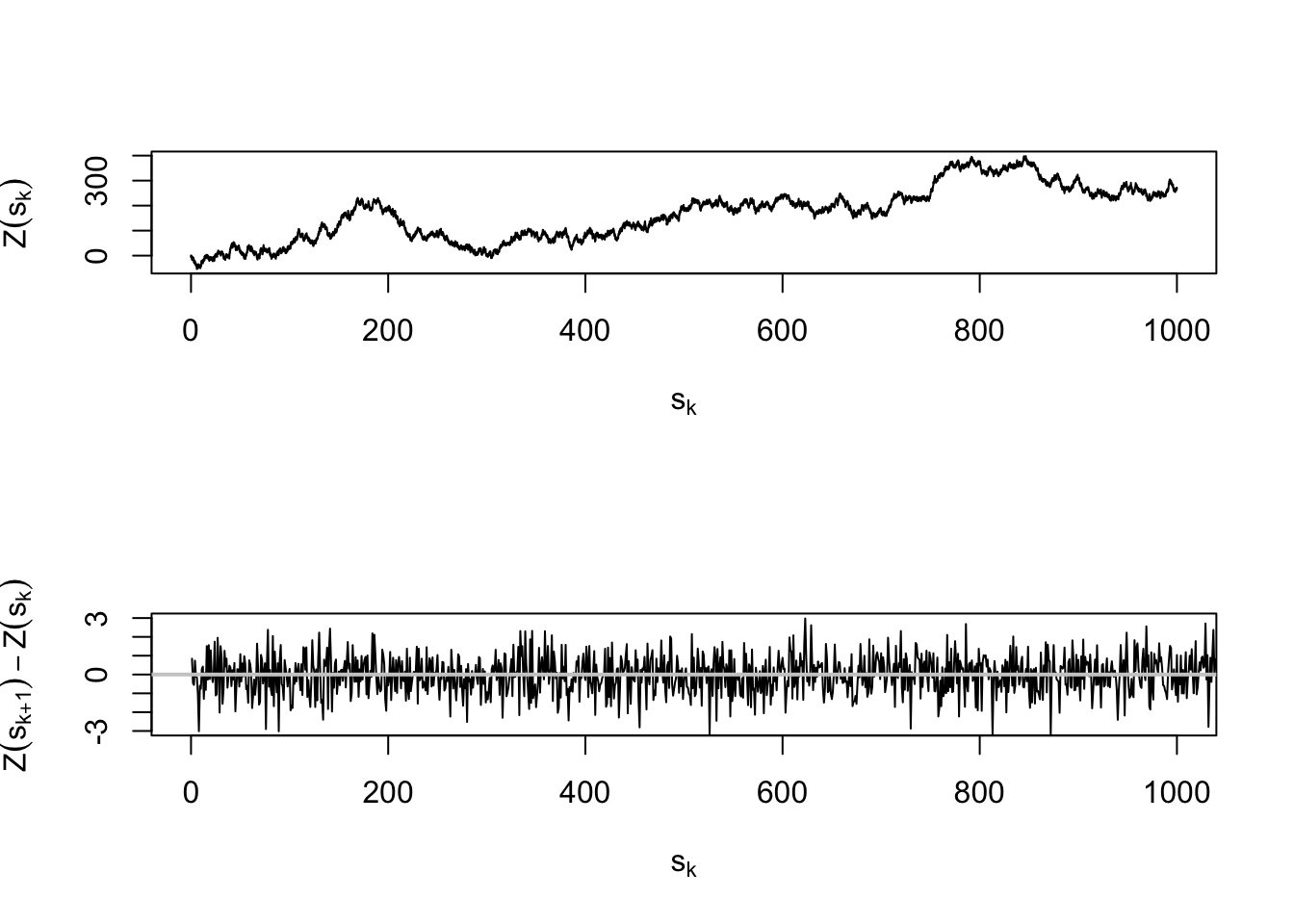
Figura 2.4: Panel superior: Realización de un proceso de Wiener-Lévy. Panel inferior: Incrementos de primer orden de la realización del proceso de Wiener-Lévy anterior.
2.3.5 Funciones aleatorias no estacionarias
Definición 2.12 (No estacionariedad).
Un campo aleatorio \(\{Z(s), s \in D\}\) es no estacionario cuando su media y/o su función de covarianza dependen de la localización (es decir, no son invariantes por traslación).
En otras palabras, si un campo aleatorio tiene una deriva (drift), es decir, su media no es constante y varía con la posición, entonces los incrementos de primer orden
\[ Z(s+h) - Z(s) \quad \tag{2.15} \]
también son no estacionarios.
En este caso se dice que el campo es un campo no intrínseco (algunos autores los denominan funciones aleatorias intrínsecas de orden \(k > 0\)).
2.4 Soporte
El soporte \(V\) de un campo aleatorio se refiere a la geometría de la característica representada por dicho campo.
Esta geometría puede ser un punto, un segmento, una superficie o un volumen:
- En el caso puntual, el campo representa una característica localizada.
- En los demás casos (línea, superficie, volumen), el campo representa el valor medio de la característica a lo largo de esa geometría.
En muchas aplicaciones prácticas, la variable regionalizada se mide como un promedio en un volumen o superficie.
En cambio, hay situaciones donde una medición puntual no tiene sentido (ejemplo: la porosidad de un material, que depende de la relación entre huecos y volumen total).
Por lo tanto, se distinguen dos tipos de soporte:
- Soporte puntual.
- Soporte no puntual o de bloque (en minería se usan indistintamente “bloques” para volúmenes o superficies).
Para un soporte de bloque centrado en un punto \(s\), el promedio se define como:
\[ Z_V(s) = \frac{1}{|V|} \int_V Z(s)\, ds, \quad |V| = \int_V ds \quad \tag{2.16} \]
donde la integral estocástica se entiende como un límite (en media cuadrática) de sumas de aproximación.
Consecuencias estadísticas del soporte
- A mayor tamaño del soporte, menor variabilidad en las observaciones.
- Esta relación entre soporte y distribución estadística tiene consecuencias directas en la práctica.
- El análisis de cómo cambian las propiedades al variar el soporte recibe el nombre de problema del cambio de soporte (change of support problem).
Además, es habitual distinguir entre:
- Predicción en un punto no observado (point support prediction).
- Predicción en un bloque no observado (block support prediction).
Code
# --- 1) Simular un campo gaussiano con GeoModels (Matern) ---
set.seed(123)
# Malla regular (n1 x n2)
n1 <- 120; n2 <- 120
x <- seq(0, 100, length.out = n1)
y <- seq(0, 100, length.out = n2)
grid <- expand.grid(x = x, y = y)
# Parámetros del covariograma
sigma2 <- 1 # varianza
range <- 12 # rango (escala)
smooth <- 0.8 # parámetro nu de Matérn
nugget <- 0.05 # nugget
mean <- 1
# Supongamos que devuelve un vector z con longitud n1*n2:
sim <- GeoModels::GeoSim(
coordx = as.matrix(grid),
corrmodel = "Matern",
param = list(scale = range, smooth = smooth,mean = mean,sill = sigma2, nugget = nugget),
progress=FALSE
)
# Intenta obtener el campo simulado; adapta si tu objeto es distinto:
z <- if (!is.null(sim$data)) sim$data else if (!is.null(sim$z)) sim$z else as.numeric(sim)
stopifnot(length(z) == n1 * n2)
# Matriz puntual (soporte punto)
Z_point <- matrix(z, nrow = n1, ncol = n2, byrow = FALSE)
# --- 2) Promedio por bloques (soporte de bloque) ---
# Tamaño del bloque (en celdas). p.ej., 4x4 celdas ≈ ventaneo espacial
bx <- 4; by <- 4
n1b <- floor(n1 / bx)
n2b <- floor(n2 / by)
block_average <- function(M, bx, by) {
n1 <- nrow(M); n2 <- ncol(M)
n1b <- floor(n1 / bx); n2b <- floor(n2 / by)
Mb <- matrix(NA_real_, nrow = n1b, ncol = n2b)
for (i in seq_len(n1b)) {
for (j in seq_len(n2b)) {
r <- ((i-1)*bx + 1):(i*bx)
c <- ((j-1)*by + 1):(j*by)
Mb[i, j] <- mean(M[r, c], na.rm = TRUE)
}
}
Mb
}
Z_block <- block_average(Z_point, bx, by)
# --- 3) Métricas comparativas ---
mean_point <- mean(Z_point)
var_point <- var(as.vector(Z_point))
mean_block <- mean(Z_block)
var_block <- var(as.vector(Z_block))
reduction <- 1 - (var_block / var_point)
# --- 4) Gráficos comparativos ---
op <- par(mfrow = c(1, 2), mar = c(3.2, 3.2, 2.2, 4.8), xaxs = "i", yaxs = "i")
image(x, y, Z_point, asp = 1, main = "Soporte puntual",
xlab = "x", ylab = "y")
# Barra de color
zlim <- range(Z_point, Z_block, finite = TRUE)
image.plot_args <- list(legend.only = TRUE, zlim = zlim)
if (requireNamespace("fields", quietly = TRUE)) {
fields::image.plot(legend.only = TRUE, zlim = zlim)
}
xb <- x[seq(1, n1, by = bx)][1:n1b]
yb <- y[seq(1, n2, by = by)][1:n2b]
image(xb, yb, Z_block, asp = 1, main = sprintf("Soporte de bloque (%dx%d)", bx, by),
xlab = "x", ylab = "y")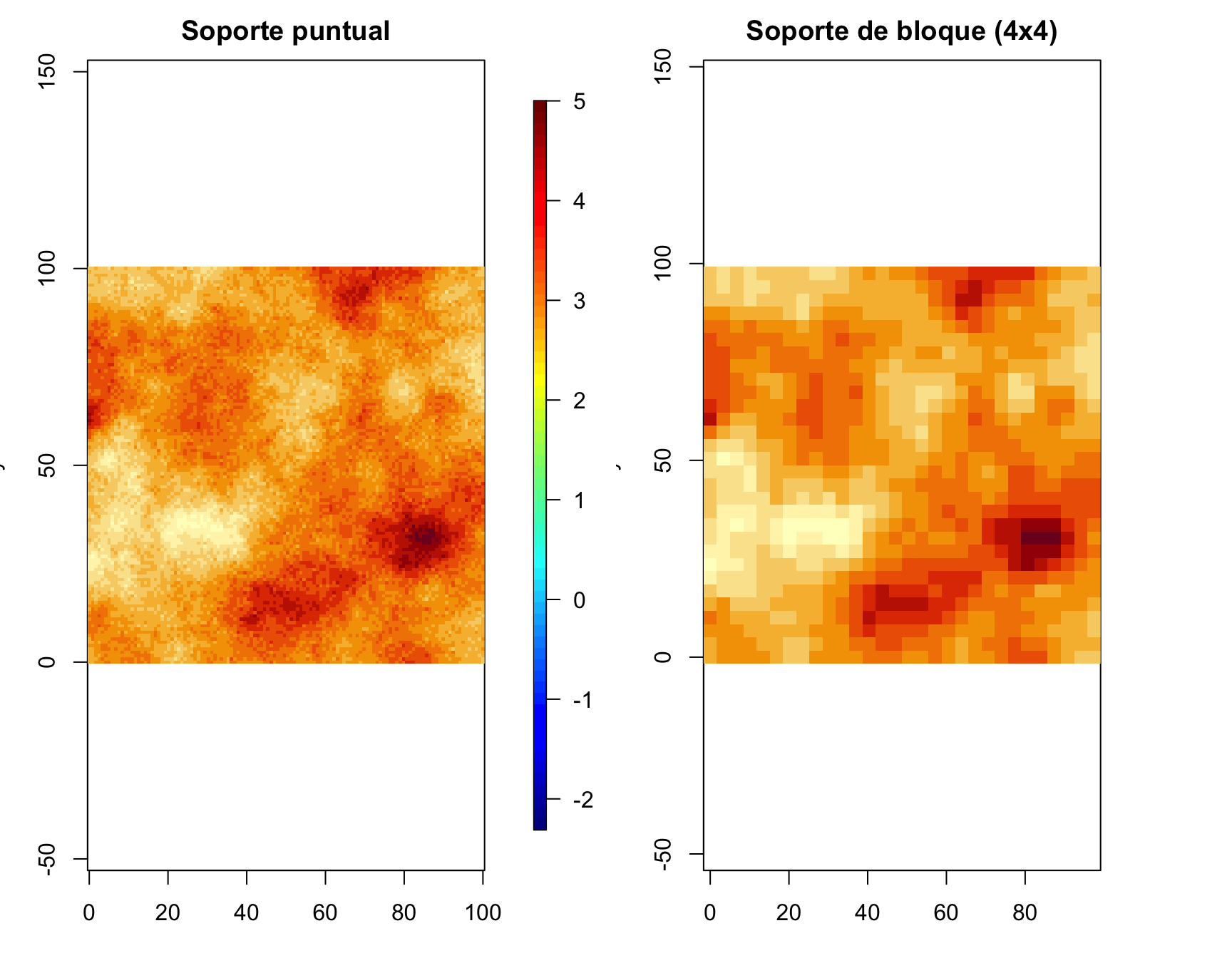
Figura 2.5: Comparación de soporte puntual vs. soporte de bloque usando un campo gaussiano simulado con GeoModels. Izquierda: realización puntual. Derecha: promedio por bloques (downscaling por promedio).
Code
par(op)
# --- 5) Resumen en consola ---
cat("\nResumen soporte puntual vs. soporte de bloque\n",
sprintf(" Media (punto): %.4f", mean_point), "\n",
sprintf(" Var (punto): %.4f", var_point), "\n",
sprintf(" Media (bloque): %.4f", mean_block), "\n",
sprintf(" Var (bloque): %.4f", var_block), "\n",
sprintf(" Reducción de varianza por bloque: %.1f%%", 100*reduction), "\n"
)##
## Resumen soporte puntual vs. soporte de bloque
## Media (punto): 1.0927
## Var (punto): 1.0503
## Media (bloque): 1.0927
## Var (bloque): 0.9602
## Reducción de varianza por bloque: 8.6%Como se observa en la Figura 2.5, el promedio por bloques reduce la variabilidad (aquí, una reducción de 8.6%) respecto al soporte puntual.