Chapter 3 Linear Regression

3.1 Introduction

In this lesson, we will explore how to use linear regression to not only understand, but to also predict relationships between variables.

Everyone loves pizza (cowabunga!) and like many pizza establishments, we will be trying to answer the question:

Can we predict the amount of pizza sold based on its price?

We’ll use a dataset called Pizza Prices.xlsx, which contains weekly pizza sales and pricing data.

3.2 Loading Our Data

We start by importing the necessary packages, reading in our Excel file, and quickly doing an overview of the data.

library(tidyverse)
library(readxl)
pizza_sales<- read_xlsx("Pizza Prices.xlsx")

library(skimr)
skim(pizza_sales)

Table 3.1: Data summary

Name	pizza_sales
Number of rows	156
Number of columns	3
_______________________
Column type frequency:
numeric	3
________________________
Group variables	None

Variable type: numeric

skim_variable	n_missing	complete_rate	mean	sd	p0	p25	p50	p75	p100	hist
Week	0	1	78.50	45.18	1.00	39.75	78.50	117.25	156.00	▇▇▇▇▇
Total Volume	0	1	88023.50	22863.94	55031.00	74347.00	83889.00	95113.00	227177.00	▇▃▁▁▁
Total Price	0	1	2.66	0.13	2.31	2.58	2.67	2.75	2.96	▁▃▇▆▂

3.3 Cleaning Our Data

library(janitor)
# Let's get rid of any spaces in the column names
pizza_sales<- clean_names(pizza_sales)
# Right now, we just want to see the relationship between volume and price, so week does not matter
pizza_sales<- pizza_sales %>% select(-1)
# Let's rename our column names to make things easier
pizza_sales <- pizza_sales %>%
  rename(price = total_price, volume = total_volume)

We now have a cleaner dataset we can use.

3.4 Visualizing Relationships

As emphasized in every chapter, it is imperative that we first graph our data to see what it looks like before we run any statistical analyses. Visuals really help us understand our data. Is our data linear? Can we see any patterns? Let’s find out!

For regression models, we use scatterplots. For a scatterplot, all we need are two numerical variables.

# Now, let us graph our data using ggplot
# As always with ggplot, we have our data, our aesthetics, and our geometry.
pizza_plot<- ggplot(pizza_sales, aes(x = price, y = volume)) +
  geom_point(size = 3)  +
  geom_smooth(method = "lm", se = FALSE) + # this adds a "line of best fit"
  theme_minimal() +
  labs(
    title = "Analysis of Pizza Sales",
    subtitle = "You know the rule, one bite...",
    x = "Price ($)", y = "Volume"
  )

pizza_plot

## `geom_smooth()` using formula = 'y ~ x'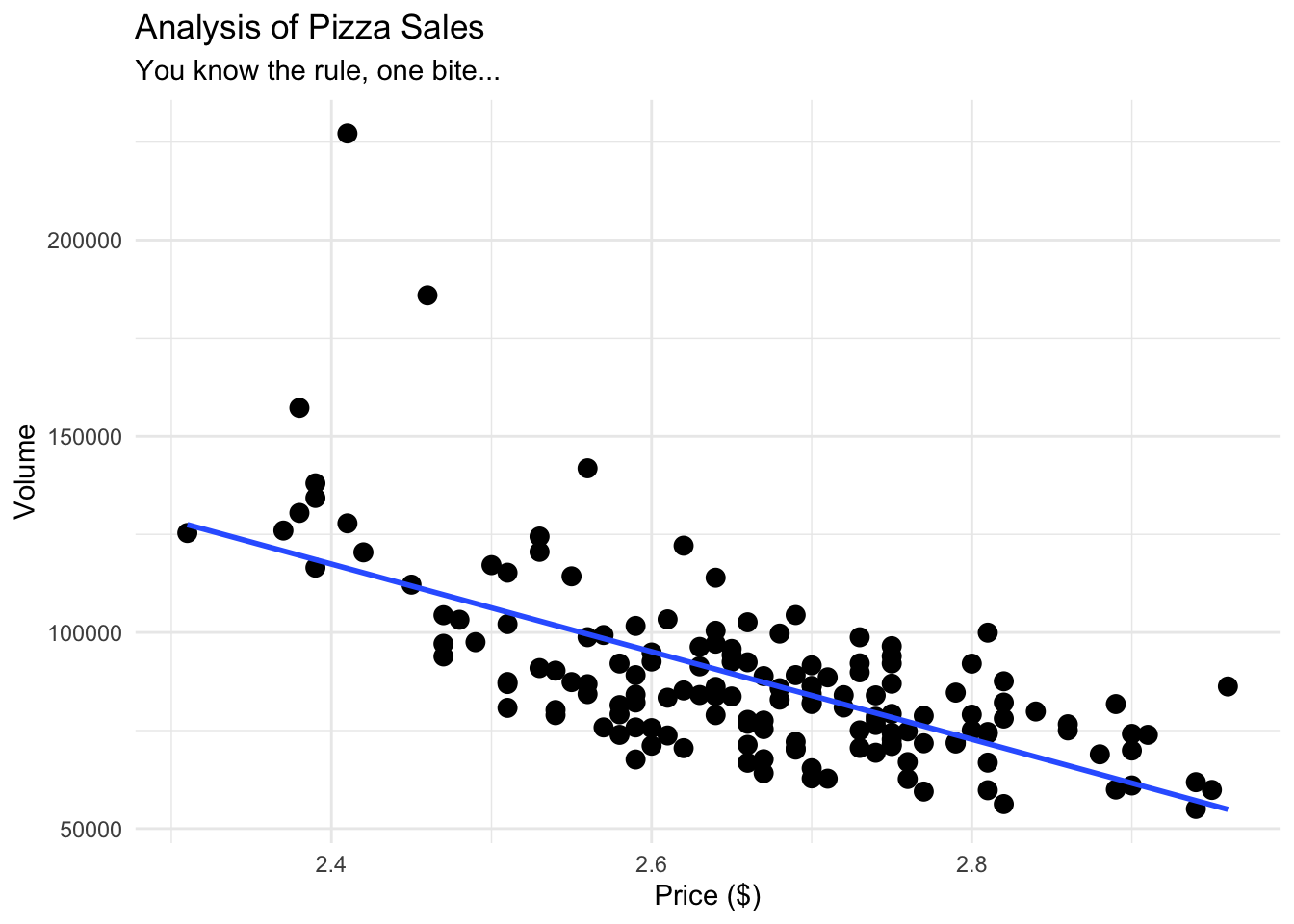

If we wanted to use another package instead of ggplot, we could also use the library ggformula.

library(ggformula)
pizza_plot_ggformula<- gf_point(volume ~ price, data=pizza_sales) %>% gf_lm(color ="purple")

pizza_plot_ggformula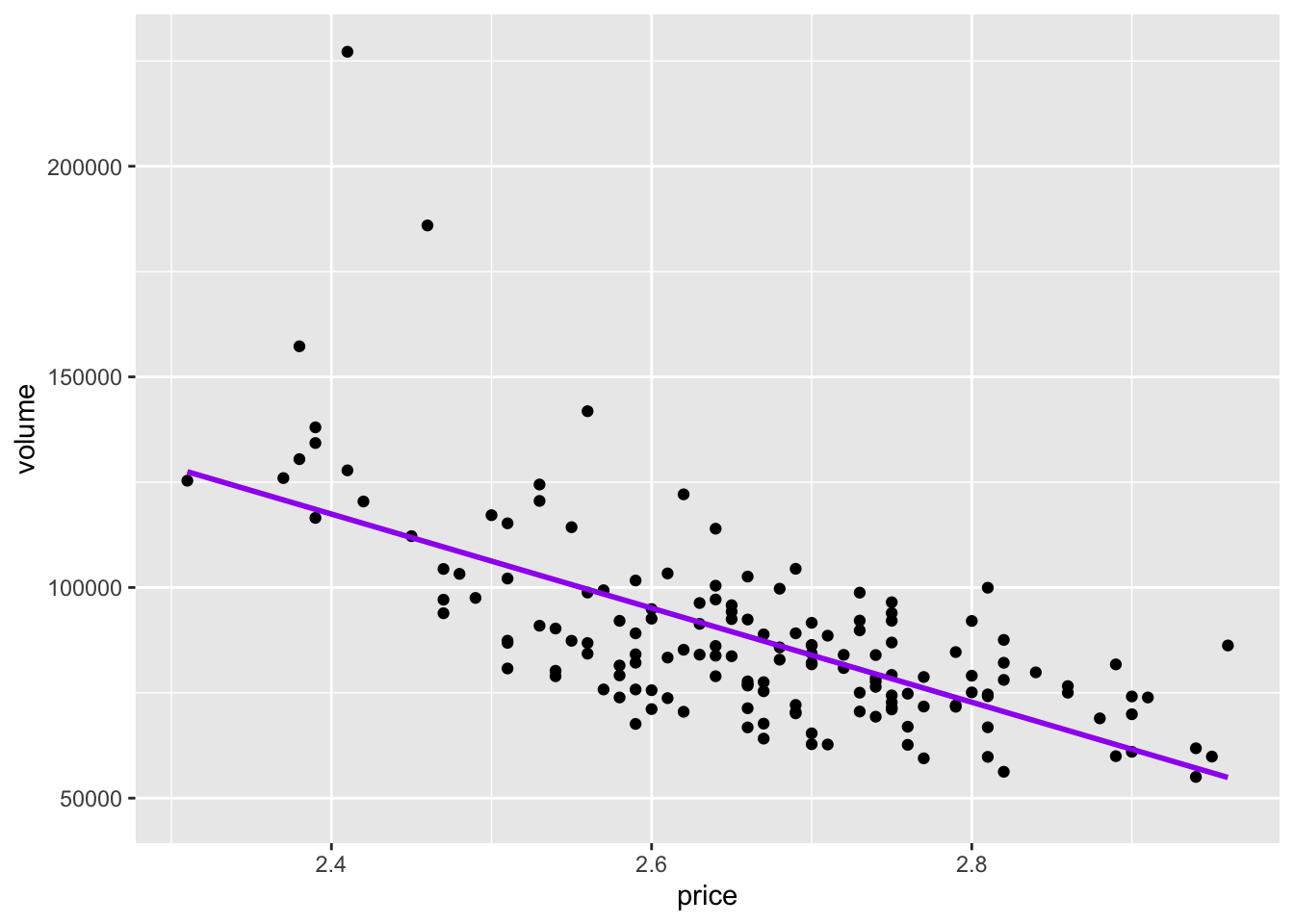

Here is a side by side comparison of what they look like. Very similar indeed.

library(patchwork)
pizza_plot + pizza_plot_ggformula

## `geom_smooth()` using formula = 'y ~ x'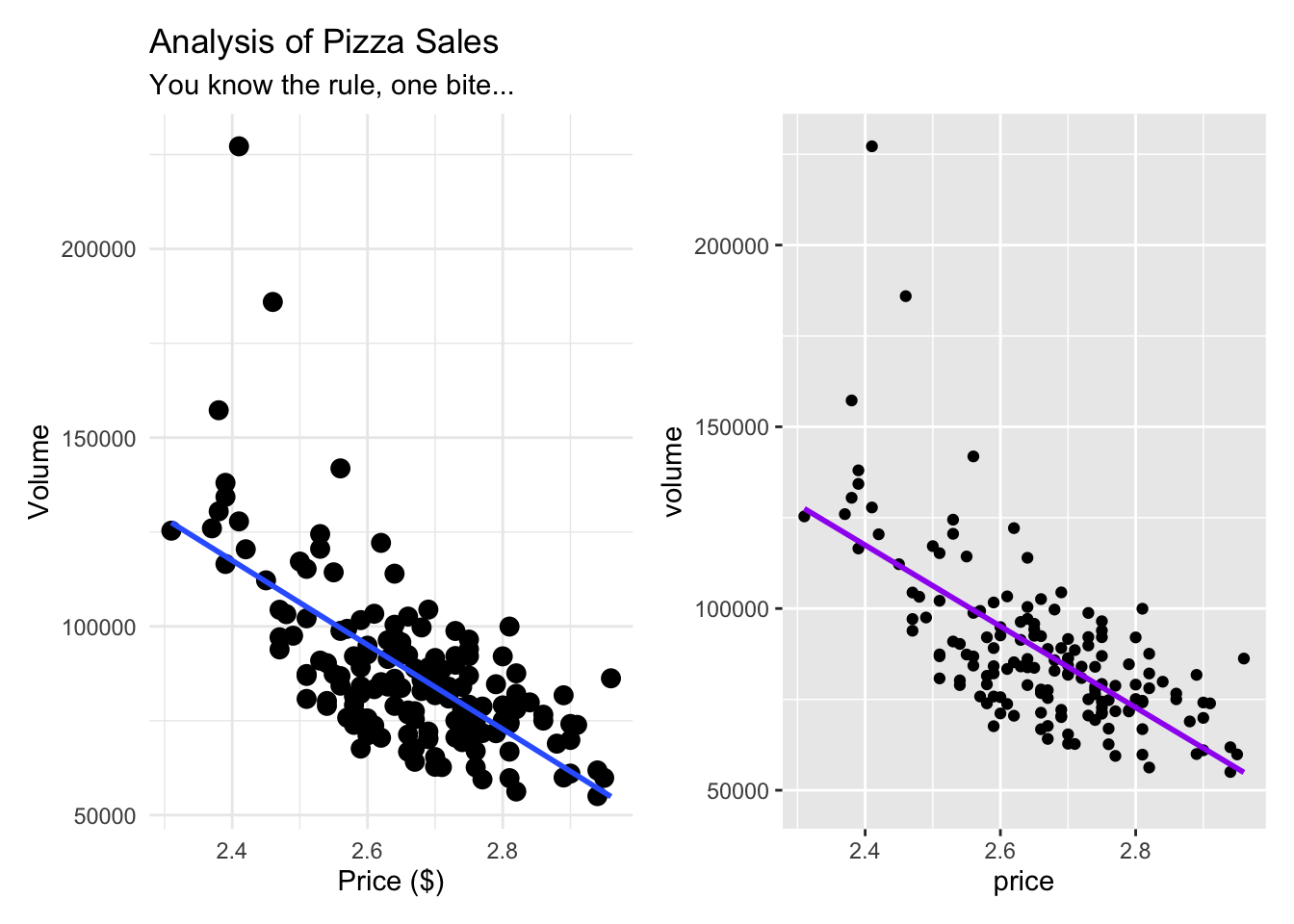

Our data is already telling us a lot. From both of our graphics, we can see that as price is going up, volume is going down, indicating a negative correlation. Our line also seems pretty straight, indicating what seems to be a moderately strong correlation.

3.5 Understanding Correlation

Before we get to a linear regression, it is best to first understand how (if at all) our variables are correlated with each other. We are first trying to figure out what variables, if any, should be included in our linear regression model, and this is exactly where correlation comes into play.

cor.test(pizza_sales$volume,pizza_sales$price)

## 
##  Pearson's product-moment correlation
## 
## data:  pizza_sales$volume and pizza_sales$price
## t = -10.8, df = 154, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  -0.7375315 -0.5567684
## sample estimates:
##        cor 
## -0.6564736

When we run a correlation, we are looking for three things: 1. The direction: is a positive or negative interaction? 2. The strength: how close is it to -1, 0, 1? 3. The p-value: Is it statistically significant?

The code above answers all three questions 1. The direction: is negative. 2. The strength: about −0.66, indicating a moderately strong negative correlation. 3. The p-value: < 0.05 indicates that the relationship between price and volume is unlikely due to chance.

With a correlation coefficient of -0.66, we have a moderately strong negative correlation between price and volume. As price goes up, volume goes down - just what we saw in our graphs!

3.6 Linear Regression Model

We have identified that there is a significant negative correlation between the two variables. Since we want to be able to predict the amount (volume) of pizza sold using price, our next step is to run a linear regression model.

With a linear regression model, we are trying to build the line of best fit and figure out the equation for the line. The formula for a line is y = mx+b, where: - y is the predicted value (in this case, volume) - m is the slope - x is the given value (in this case, price) - b is the y intercept (the y value when x is 0)

When we are able to get the slope and the intercept, we can then begin to predict values.

To run a linear regression model, we can use the lm command. It follows the structure: - lm(y ~ x, data = dataset) - lm(what we want to predict ~ the predictor, data = our dataset)

pizza_lm<- lm(volume ~ price, data=pizza_sales)
# The code above is saving our linear regression model as pizza_lm
summary(pizza_lm)

## 
## Call:
## lm(formula = volume ~ price, data = pizza_sales)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -28602 -11685  -1824   8379 110857 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   385442      27575   13.98   <2e-16 ***
## price        -111669      10340  -10.80   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 17300 on 154 degrees of freedom
## Multiple R-squared:  0.431,  Adjusted R-squared:  0.4273 
## F-statistic: 116.6 on 1 and 154 DF,  p-value: < 2.2e-16

# When we call summary on our model, we can find out our key insights

Congratulations! We have just run our first linear regression model! We have some key insights, including:

• Intercept: 385,442. This is our b value on our line equation. This means that when the price of pizza is 0 (free pizza would be nice, but really just a dream), the y value would be 385442.
• price: -111,669. This is our slope, or our m value on our line equation. This tells us that for every price point increase, to decrease our volume by -111,669. This makes sense, since we have a negative correlation.
• Multiple R-squared: As we have seen before, this tells us how much of the variability our model explains. For our example, about 43% of the variance in pizza sales volume is explained by price alone. Warning: Multiple R-squared in linear regression models always increases with each new predictor added to a model, regardless of how potent it is.
• Adjusted R-squared: This is almost identical to the Multiple R-squared value, except that it takes into account each new predictor added, and does not go up just because a new predictor was added to the model.
• p-value: There are three p-values here. The first two, on the intercept and price lines, indicate if the relationships are statistically significant, which they are. The bottom one is if the model itself is significant, which it is.
• F-statistic: This tells us how strong our model is. 116.6 is a high value.

All of these insights together mean that this is a very good model to predict volume of pizza sold.

In R, we always want to explore different packages. The broom package in R is very helpful when making statistical objects into nicer tibbles.

# If we want to get the same information from our lm model using a different package
library(broom)
tidy(pizza_lm)

## # A tibble: 2 × 5
##   term        estimate std.error statistic  p.value
##   <chr>          <dbl>     <dbl>     <dbl>    <dbl>
## 1 (Intercept)  385442.    27575.      14.0 3.44e-29
## 2 price       -111669.    10340.     -10.8 1.36e-20

glance(pizza_lm)

## # A tibble: 1 × 12
##   r.squared adj.r.squared  sigma statistic  p.value    df logLik   AIC   BIC
##       <dbl>         <dbl>  <dbl>     <dbl>    <dbl> <dbl>  <dbl> <dbl> <dbl>
## 1     0.431         0.427 17303.      117. 1.36e-20     1 -1743. 3491. 3501.
## # ℹ 3 more variables: deviance <dbl>, df.residual <int>, nobs <int>

Our finalized equation is y (-111,669 * price) + 385,442. All we need to do is plug in any price value, and we can predict the volume of pizza sold.

3.7 Checking the residuals

Now, we need to make sure that our data for the line looks good, answering the question:

How close are our predicted values to our actual values?

To answer this question, we need to figure out the predicted values and then their residuals (the difference between the actual vs the predicted value).

We can do this in R with the two commands below.

pizza_sales <- pizza_sales %>%
  mutate(predicted = predict(pizza_lm),
         residuals = residuals(pizza_lm))

To visually see the difference between the actual values and the predicted values, we can create a similar scatterplot as before, but add lines connecting our line of best fit and our points.

# What if we want to see actual vs predicted on our plot?
pizza_plot_residuals<- ggplot(pizza_sales, aes(x = price, y = volume)) +
  geom_point(size = 3)  +
  geom_smooth(method = "lm", se = FALSE) +
  geom_segment(aes(xend = price, yend = predicted), color = "gray", linewidth = 0.7) + # # geom_segment is what gives us our residual lines
  theme_minimal() +
  labs(
    title = "Analysis of Pizza Sales",
    subtitle = "Gray lines show residuals (differences between actual and model predictions)",
    x = "Price ($)", y = "Volume"
  )
pizza_plot_residuals

## `geom_smooth()` using formula = 'y ~ x'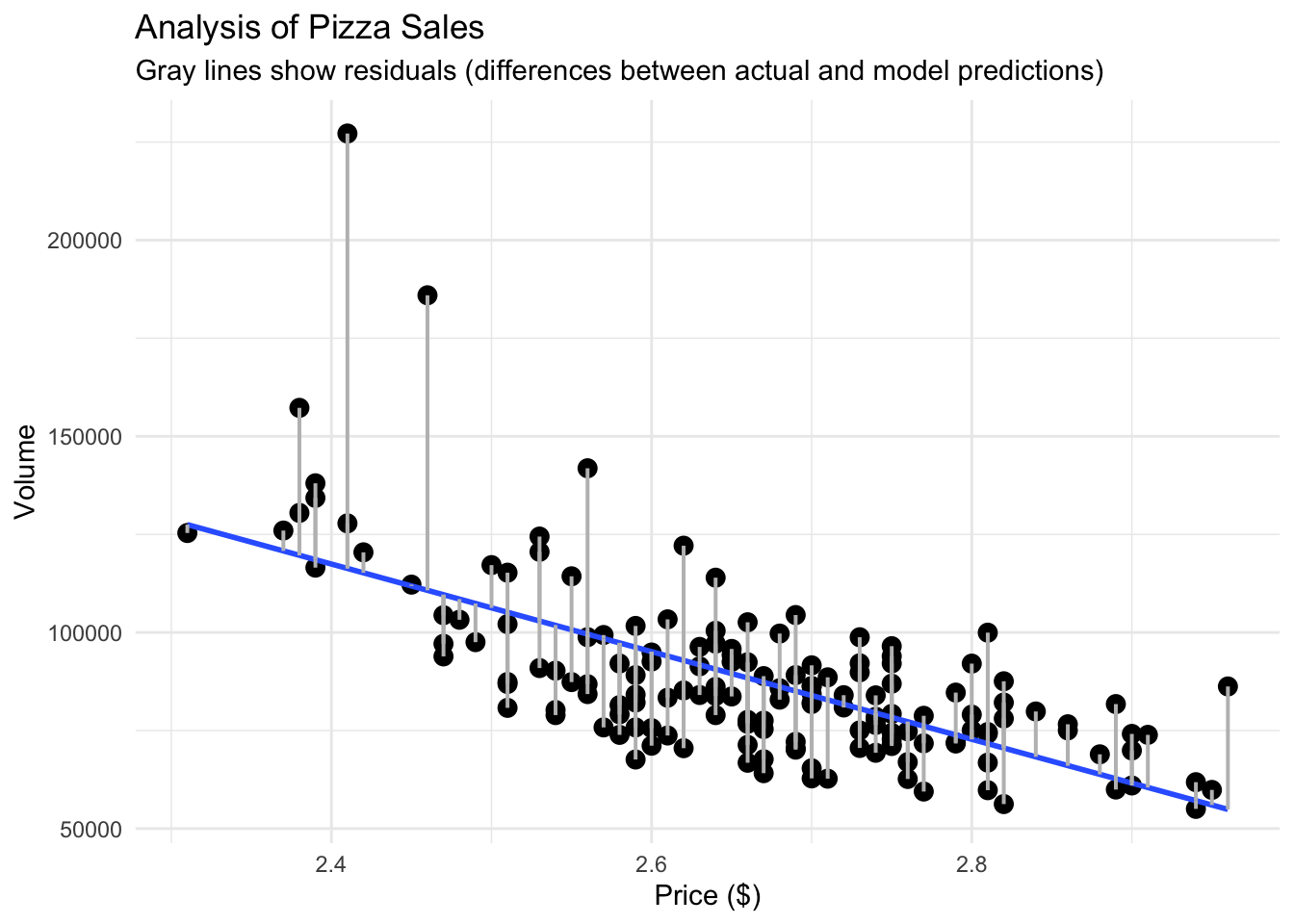

With our residuals, we want them to be random. Visually, that means that the residual values should be scattered on an x-y plane without a pattern. To see this, we can graph the residuals themselves.

# Let us graph our residuals to make sure they are random
ggplot(pizza_sales, aes(x = predicted, y = residuals)) +
  geom_point(color = "blue") +
  geom_hline(yintercept = 0, linetype = "dashed") +
  geom_smooth(se = FALSE, color = "red", linetype = "dotted")+
  labs(
    title = "Residuals Plot",
    x = "Predicted Volume",
    y = "Residuals"
  )

## `geom_smooth()` using method = 'loess' and formula = 'y ~ x'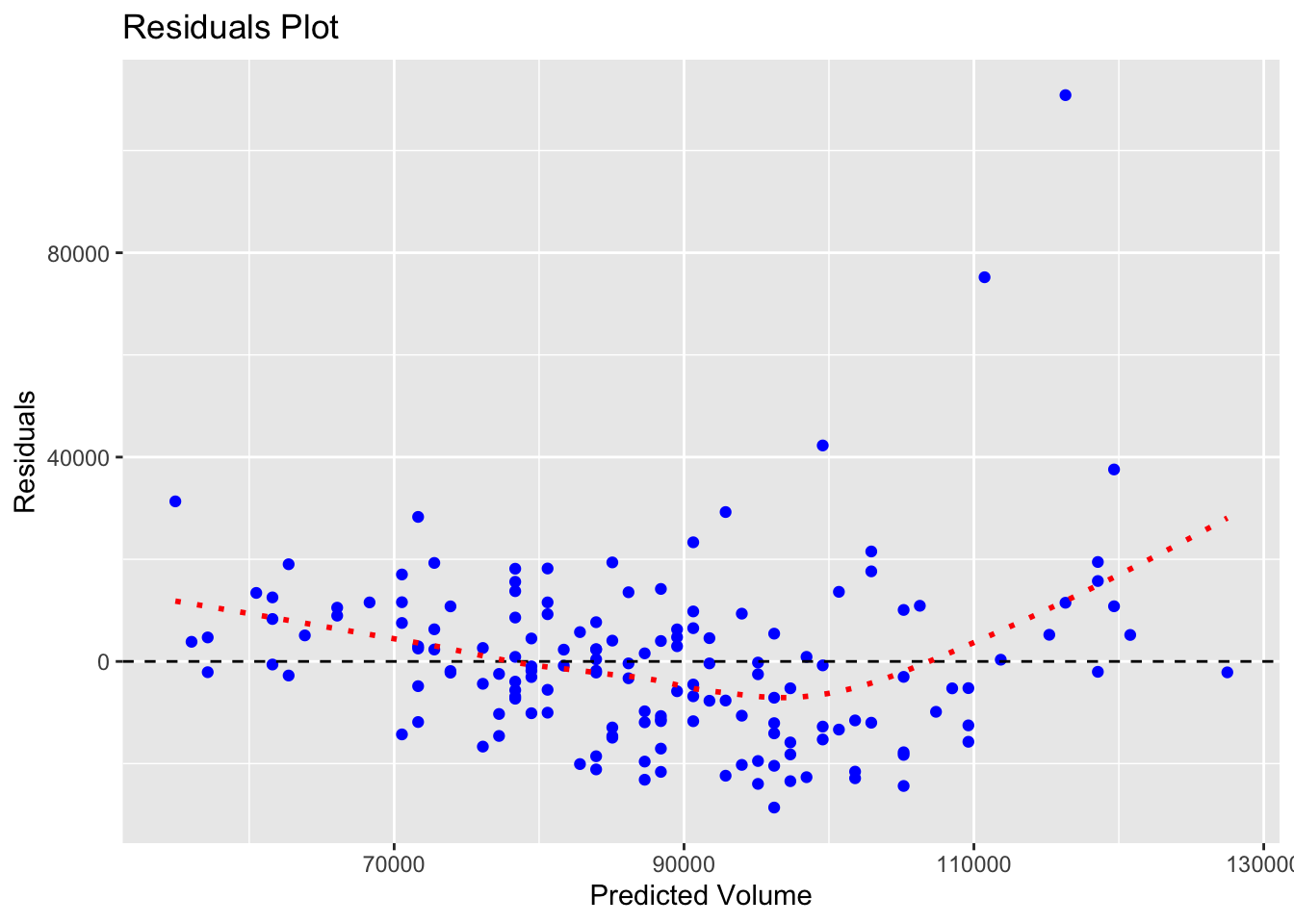

The red line in the graph above has a slight curve, showing that our model is less accurate at the extremes (low and high prices). Thankfully, this pattern isn’t very pronounced.

To accompany the visual, we want to statistically test for heteroscedasticity, meaning:

Are the residuals roughly equal in variance across all predicted values?

We will either see: - Homoscedasticity: residuals are equally spread (good) - Heteroscedasticity: residuals get wider or narrower as predictions change (bad)

The Breusch-Pagan test provides insights for this.

library(lmtest)
bptest(pizza_lm)

## 
##  studentized Breusch-Pagan test
## 
## data:  pizza_lm
## BP = 7.7392, df = 1, p-value = 0.005403

The main focus point here is the p-value: - > 0.05 Fail to reject H₀ → residuals are homoscedastic (good) - < 0.05 Reject H₀ → residuals are heteroscedastic (not ideal)

Since our p-value is less than .05, our residuals are heteroscedastic.

This does not invalidate our model, and for right now, we do not need to change it. It is just showing us that it is not perfect, and not all prices predict equally well. In reality, this might happen if higher-priced pizzas are sold less frequently, giving us fewer data points and more variability.

Congratulations, we have just completed our first linear regression model!

3.8 Adding more variables

Throughout this chapter, we have only looked at 2 variables: price and volume to see if the former can predict the latter. But, what if we have more variables? Can we also utilize them in our regression model?

Let’s find out!

Let us create two new variables to add to our data: one where David Portnoy visited the pizza shop and another on how much was spent on advertising.

# Now, let's add some other variables to our data
set.seed(42)

# 1) Dave Portnoy visit.
pizza_sales <- pizza_sales %>%
  mutate(portnoy_visit = rbinom(n(), size = 1, prob = 0.06))  # about 3–6% of weeks

# 2) Ad spend
pizza_sales <- pizza_sales %>%
  mutate(ad_spend = round(runif(n(), 800, 6000), 0))

Now, since we have multiple variables, we can run what’s called multivariate regression model. To add more predictors, we simply use the + sign in our lm command after our first predictor.

m1 <- lm(volume ~ price, data = pizza_sales)                      # baseline
m2 <- lm(volume ~ price + portnoy_visit, data = pizza_sales)      # add portnoy visit
m3 <- lm(volume ~ price + ad_spend, data = pizza_sales)           # add ad spending
m4 <- lm(volume ~ price + ad_spend + portnoy_visit, data = pizza_sales)  # both

Boom! In the code above, we have now run 4 regression models, with every combination included.

Now, we can run the summary or glance command on each model individually, compare the models manually, but that would require a lot of working memory power on our end. Or we could utilize some commands in R to make our lives much easier.

# How do we know which model is the best?
library(AICcmodavg)
AIC(m1, m2, m3, m4) %>% arrange(AIC)

##    df      AIC
## m2  4 3486.244
## m4  5 3488.239
## m1  3 3491.395
## m3  4 3493.327

# This code provides us with an AIC (Akaike Information Criterion) value.
# The smaller the AIC, the better the model’s trade-off between complexity and fit.

# Let's say we want to use the broom function again to do a model comparison
models <- list(m1, m2, m3, m4)
# In the code above, we are taking all of our models and putting them into a "list" of models
names(models) <- c("m1","m2","m3","m4")
# In the code above, we are just giving each item in the list a name

# In the code below, we are saying "Hey, run glance on every single item on the models list and create a data frame

map_df(models, ~glance(.x), .id = "model") %>% select(model, r.squared,adj.r.squared,p.value,AIC)

## # A tibble: 4 × 5
##   model r.squared adj.r.squared  p.value   AIC
##   <chr>     <dbl>         <dbl>    <dbl> <dbl>
## 1 m1        0.431         0.427 1.36e-20 3491.
## 2 m2        0.456         0.449 5.57e-21 3486.
## 3 m3        0.431         0.424 1.79e-19 3493.
## 4 m4        0.456         0.446 5.07e-20 3488.

With both of these, we now have: 1. R^2: A higher R squared means the model is a better predictor. Remember, R^2 always goes up with each added predictor, no matter how salient they actually are. 2. Adjusted R^2: A higher adjusted R squared means the model is a better predictor. Adjusted R^2 always takes into account the number of predictors and does not inherently increase with more predictors. 3. p-value: If these models are statistically significant. 4. AIC: tells us how good our models are. A lower number means a better model.

Overall, the goal is to create the most parsimonious regression model as possible. That is, the model with the fewest necessary predictors. As such, the model that is most parsimonious is m1, the model with just price. Yes, other models have higher adjusted R^2 values and lower AIC numbers, but only slightly. In this case, m1 is the model to go with.

3.9 Conclusion

Congratulations! You have successfully run correlations (to help see what variables we want to build our regression model with), regression models, multiple regression models, compared models, and even analyzed the differences between our actual values and our predicted values.

Don’t underestimate how powerful regression models can be. With a line equation, you can help predict any variable!

3.10 Key Takeaways

• Linear regression helps us predict one variable (Y) from another (X) using a line of best fit.
• The equation of the line is y = mx + b, where:
  • m = slope (how much Y changes for every 1-unit change in X)
  • b = intercept (the value of Y when X = 0)
• The slope tells us both the direction and strength of the relationship.
• Residuals = actual - predicted values; smaller residuals = better model fit.
• A good model has random, evenly scattered residuals (homoscedasticity).
• R² tells us how much variance in Y is explained by X.
• Adjusted R² penalizes unnecessary predictors in multiple regression models.
• AIC helps compare models: lower AIC = better balance between fit and simplicity.
• Parsimonious models (simpler ones that still explain the data well) are preferred.
• Stepwise regression automatically selects the most parsimonious model using AIC.
• Correlation shows association; regression goes further by predicting and quantifying impact.
• Always visualize both your model fit and your residuals before interpreting results!

3.11 Checklist

When running linear regressions, have you:

• Loaded and inspected your data (skim, summary, str)
• Cleaned and renamed your variables as needed
• Graphed your variables with scatterplots and trend lines
• Checked that the relationship looks linear
• Calculated correlations before fitting your model
• Built your model using lm(y ~ x)
• Examined coefficients (intercept and slope) and their significance
• Computed predicted values and residuals
• Graphed residuals to ensure randomness (no U-shape or funnel)
• Tested for homoscedasticity using bptest() (Breusch–Pagan test)
• (Optional) Checked residual normality with a histogram or QQ plot
• Interpreted R² and Adjusted R² to describe model performance
• Added additional predictors for multiple regression if needed
• Compared models using AIC or stepwise regression
• Selected the most parsimonious model (best fit with the least complexity)
• Clearly interpreted what the slope and intercept mean in real-world terms
• Reported results visually (scatterplot, line of best fit, residual plot)

3.12 Bonus code

If you are looking to compare multiple regression models in a faster way, you could also utilize the code below.

full_model <- lm(volume ~ price + ad_spend + portnoy_visit, data = pizza_sales)
step_model <- step(full_model, direction = "both")

## Start:  AIC=3043.53
## volume ~ price + ad_spend + portnoy_visit
## 
##                 Df  Sum of Sq        RSS    AIC
## - ad_spend       1 1.4575e+06 4.4042e+10 3041.5
## <none>                        4.4041e+10 3043.5
## - portnoy_visit  1 2.0473e+09 4.6088e+10 3048.6
## - price          1 3.1199e+10 7.5240e+10 3125.1
## 
## Step:  AIC=3041.54
## volume ~ price + portnoy_visit
## 
##                 Df  Sum of Sq        RSS    AIC
## <none>                        4.4042e+10 3041.5
## + ad_spend       1 1.4575e+06 4.4041e+10 3043.5
## - portnoy_visit  1 2.0659e+09 4.6108e+10 3046.7
## - price          1 3.1252e+10 7.5294e+10 3123.2