Section 8 Etude de cas

8.1 Détermination d’une pluie de bassin

Cette activité mobilise les notions vues dans la section “Précipitations”. Les acquis d’apprentissage visés sont :

Appliquer différentes méthodes de spatialisation de la pluie
Comparer les différentes méthodes et être en mesure d’interpréter ces différences
Appliquer une méthodologie de validation croisée

Cette activité mobilise aussi vos compétences en systèmes d’information géographique.

8.1.1 Contexte de l’étude de cas proposée

La détermination d’une pluie spatiale à l’échelle d’un bassin versant est importante pour beaucoup d’applications hydrologiques. Elle peut se faire de multiples façons et il n’est pas toujours évident de déterminer a priori quelle méthode est la plus pertinente pour cette estimation sur un bassin versant donné car cela dépend de la variabilité spatiale de la pluie qui dépend elle-même des caractéristiques climatiques et topographiques du bassin versant.
Le but de cette étude de cas est de comparer quelques-unes de ces méthodes sur un bassin versant à gradient altimétrique modéré. Les méthodes existantes à tester sont exposées dans nombre d’ouvrages (Hingray et al., 2009) et des comparaisons similaires sont courantes dans la littérature hydrologique (Bourgin et al., 2012 ; Renard et Comby, 2006).

8.1.2 Méthodologie et données

Cette section détaille les données que vous pouvez utiliser et les méthodes à suivre.

8.1.2.1 Etapes de l’étude de cas

Vous pourrez suivre la démarche suivante : * Détermination de la pluie de bassin à partir des informations pluviométriques ponctuelles par différentes techniques (polygones de Thiessen, Inverse distance weighting, isohyètes, gradient d’altitude)

Comparaison avec des estimations de produits maillés (réanalyses Météo-France SAFRAN, Vidal et al. 2010)
Évaluation des méthodes par une démarche de validation croisée

Ces différentes étapes marqueront les différentes taches à réaliser pour cette étude de cas

8.1.2.2 Données mobilisées pour l’étude de cas

Les données de précipitations aux stations ont été extraites de la base de données de climatologie quotidienne de Météo-France (https://www.data.gouv.fr/fr/datasets/donnees-climatologiques-de-base-quotidiennes/) et les données de contours de bassins et de pluie SAFRAN à partir du jeu de données CAMELS-FR (https://doi.org/10.57745/WH7FJR).

L’outil de visualisation de données a été développé avec le package R Shiny. Cet outil vous permet de choisir et visualiser le bassin versant que vous allez étudier, de visualiser les données (observations aux stations pluviométriques et pluies de bassin par la réanalyse SAFRAN) de ce bassin, et de télécharger ces données sur votre ordinateur en local afin de faire les calculs nécessaires. Pour un rendu optimal, ouvrez dans un nouvel onglet en cliquant ici

8.1.3 A vous de jouer…

8.1.3.1 Etape 0 : Choisissez votre bassin versant et charger les données nécessaires

Vous avez le choix entre 27 bassins versants situés dans différents contextes climatique et géographique. L’outil de visualisation des données vous permettra de charger les données nécessaires.

Pour plus d’informations sur le site choisi, vous pouvez consulter le site Hydroportail (https://hydro.eaufrance.fr/) qui vous permettra de trouver le nom de la rivière à partir du code de la station hydrométrique.

8.1.3.2 Etape 1 : Déterminez les pluies de bassin à partir de méthodes de spatialisation

A minima, vous devez tester les méthodes classiques suivantes :

Pluie moyenne arithmétique ;
Pluie moyenne de bassin par la méthode des polygones de Thiessen ;
Pluie moyenne de bassin par la méthode d’inverse distance ;
Pluie moyenne de bassin par la méthode du gradient d’altitude.

Pour chacune des méthodes, l’estimation portera sur la pluie moyenne pluriannuelle, à partir des pluies moyennes des postes pluviométriques (Tableau 1). Ces méthodes sont décrites dans les références citées précédemment, seules les données nécessaires et les hypothèses possibles pour mener à bien le projet sont proposées ci-après.

Pluie moyenne arithmétique

Vous devez faire le choix des postes pluviométriques à prendre en compte pour le calcul de la moyenne. Cette méthode basique ne permet pas de spatialiser la pluie au sens strict et ne sera donc pas mobilisable pour l’étape de validation croisée.

Pluie moyenne de bassin par la méthode des polygones de Thiessen

Le calcul de la pluie moyenne par la méthode des polygones de Thiessen peut se faire par l’utilisation d’un Système d’Information Géographique (QGIS) ou de langage de programmation permettant l’analyse spatiale (Python, R). Pour ce faire, vous aurez besoin des fichiers d’information spatiale de contour de bassin et de position des postes pluviométriques, disponible en téléchargeant les données sur le serveur Shiny de visualisation des données.

Pluie moyenne de bassin par la méthode d’inverse distance

Le calcul de la pluie moyenne par la méthode de l’inverse distance peut aussi se faire par l’utilisation d’un Système d’Information Géographique (SIG). Cette méthode nécessite un quadrillage de l’espace et des calculs de type raster. Vous pourrez utiliser le quadrillage du Modèle Numérique de Terrain (à 1km ou à plus haute résolution) disponible en téléchargeant les données sur le serveur Shiny de visualisation des données.

Pluie moyenne de bassin par la méthode du gradient d’altitude

Cette méthode s’appuie sur la relation entre la pluie moyenne annuelle et l’altitude des postes pluviométriques. Vous pourrez utiliser un des deux jeux d’altitude raster pour déterminer l’altitude des postes pluviométriques. Une fois la relation Pluie = f(Altitude) établie, vous pouvez déterminer les pluies sur chaque maille de MNT et déterminer une pluie moyenne de bassin versant.

Si vous en avez le temps, n’hésitez pas à tester d’autres méthodes et à tester aussi la sensibilité des méthodes à leur paramètre, quand des paramètres rentrent en jeu (par exemple la puissance de l’approche Inverse Distance). Il est important de clore cette étape en comparant les estimations :

des pluies de bassins
des pluies spatialisées en montrant par exemple les carte de pluie moyenne annuelle.

8.1.3.3 Etape 2 : Comparaion aux données SAFRAN

Les données SAFRAN sont des données météorologiques dite de réanalyse. Cela veut dire qu’elles combinent des sorties de modèles climatiques et des observation qui sont assimilées dans le modèle. Pour les précipitations, le grand nombre de stations au sol fait que le produit de réanalyse est très proche ces observations au sol, le modèle climatique étant plus utilisé comme un interpolateur spatiale des données au sol (pour plus de détail, voir Vidal et al. 2010).

Le produit SAFRAN est un produit maillé avec des mailles de 8km de côté (64km²), ce qui peut être relativement grossier lorsque l’on travaille sur un petit bassin versant. Malgré cela, vous considérerez que la pluie SAFRAN fournie dans cette étude de cas est la référence à laquelle vous pourrez comparez vos différentes estimations de pluie de bassin.

8.1.3.4 Etape 3 : Validation croisée

Les méthodes de spatialisation des précipitations peuvent être testées dans un cadre de validation croisée. Le principe est simple :

On enlève un poste \(i\) qui a une précipitation \(P_i\) et qui est situé aux coordonnées géographiques \((x_i,y_i)\) ;
On applique une méthode de spatialisation sans le poste \(i\)
Avec cette méthode, on détermine la pluie \(\hat{P_i}\) au niveau du point \((x_i,y_i)\)
On calcule l’erreur quadratique de l’estimation \((\hat{P_i} - P_i)^{2}\)

On peut répéter cette opération en changeant le poste enlevé, ce qui permet d’avoir une évaluation globale de chaque méthode.

8.2 Impacts hydrologiques du changement climatique

Cette activité mobilise les notions de la section Evapotranspiration. Les acquis d’apprentissage visés pour cette activité sont :

Développer les sens critique de l’application d’un modèle
Connaitre et manipuler les projections climatiques issues des expériences d’intercomparaison de modèles de climat du GIEC

8.2.1 Contexte de l’étude de cas proposée

Les études d’impact hydrologique du changement climatique sont cruciales pour déterminer quelles seront les évolutions des ressources en eau dans le futur et pour envisager des stratégies d’adaptation de nos usages de ces ressources.

On prend ici le rôle du scientifique qui doit répondre à une demande des gestionnaires d’un bassin versant sur l’évolution des ressources en eau. C’est vous qui allez choisir le bassin versant d’étude. Les projections climatiques indiquent des chanegments assez diversifiés en terme de température et surtout de précipitation à l’échelle de la France. Pour cette raison, dans ce cas d’étude, nous vous proposons d’évaluer l’impact hydrologique du changement climatique sur (idéalement plusieurs) bassins versants en suivant une évaluation multi-modèle et multi-scénario.

Malgré la volonté de de proposer un cas d’étude réel, les résultats que vous pourrez obtenir dans cette activité sont bien sûr à prendre avec précaution. Nous reviendrons sur les limites de la méthodologie suivie ici dans la fin de l’activité.

On se propose dans cette activité de réaliser un cas d’étude mobilisant les différentes notions vues précédemment sur l’estimation de l’évapotranspiration à partir de données d’évapotranspiration potentielle et de précipitations.

L’objectif pédagogique est double :

Appliquer les méthodes d’estimation vues en cours
Appréhender les impacts hydrologiques du changement climatique et leur diversité en fonction des modèles utilisés et des régions étudiées.

8.2.2 Méthodologie et données

Cette section détaille les données que vous pouvez utiliser et les méthodes à suivre.

8.2.2.1 Etapes de l’étude de cas

Vous suivrez les étapes classiques d’une étude d’impact hydrologique du changement climatique :

Analyse des données historiques et détermination / optimisation du modèle hydrologique à utiliser
Analyse des biais éventuels des simulations climatiques historiques
Analyse de l’évolution climatique sur le bassin versant
Détermination des écoulements futurs en fonction des modèles de climat et des scénarios d’émission de gaz à effet de serre

Ces différentes étapes marqueront les différentes taches à réaliser pour cette étude de cas.

8.2.2.2 Données mobilisées pour l’étude de cas

Toutes les données utilisées dans le cadre de cette étude de cas sont publiques. Ces données publiques sont disponibles à l’échelle de la France et la méthodologie est donc réplicable à d’autres bassins versants.

Les données historiques d’observation de température, précipitation, débit et évapotranspiration potentielle (ETP) sont extraites de la base de données CAMELS-FR (https://doi.org/10.57745/WH7FJR). En général, on dispose des données historiques sur près de 50 ans (1971-2020).
Les simulations climatiques de température, précipitation et ETP ont été extraites à partir du site DRIAS-CLIMAT (https://www.drias-climat.fr/) qui met en ligne des projections issues du programme CMIP5 sur toute la France métropolitaine. Des multiples projections disponibles, nous avons retenu les projections de 5 modèles de climat (GCM-RCM) qui fournissent chacun 1 simulation historique (1950-2005) et 3 simulations pour le 21ème siècle (2005-2100) représetant les 3 scébarios d’émissions couramment utilisés (RCP pour Representative Concentration Pathway)
Dans l’outil de visualisation des données, nous avons inclus des représentations cartographiques des bassins versants. Les données d’altitude ont été extraites du produit SRTM et les donnes d’occupation du sol du produit Corine Land Cover. Ces deux bases de données sont en accès libre.

L’outil de visualisation de données a été développé avec le package R Shiny. Cet outil vous permet de choisir et visualiser le bassin versant que vous allez étudier, de visualiser les données (observations et simulations climatiques) de ce bassin, et de télécharger ces données sur votre ordinateur en local afin de faire les calculs nécessaires. Pour un rendu optimal, ouvrez dans un nouvel onglet en cliquant ici

8.2.3 A vous de jouer…

8.2.3.1 Etape 0 : Choisissez votre bassin versant et charger les données nécessaires

Vous avez le choix entre 36 bassins versants situés dans différents contextes climatique et géographique. L’outil de visualisation des données vous permettra de charger les données nécessaires.

8.2.3.2 Etape 1 : Déterminez votre modèle hydrologique

Les modèles d’estimation de l’évapotranspiration comme l’équation de Budyko peuvent être utilisés pour évaluer l’impact du changement climatique sur les débits moyens annuels des rivières. Le bilan hydrique sur un bassin versant s’écrit :

\(P = ET + Q + \Delta S\)

où \(P\) est la précipitation annuelle moyenne du bassin versant, \(ET\) est l’évapotranspiration moyenne annuelle et \(Q\) est l’écoulement du bassin versant et \(\Delta S\) est la variation de stock. A long-terme, la variation de stock est négligeable et le bilan s’écrit simplement :

\(P = ET + Q\)

Les modèles de bilan en eau (e.g. Budyko) permettent d’estimer \(ET\) à partir des données de précipitations \(P\) et des données d’évapotranspiration potentielle \(ETP\). L’estimation de \(ET\) permet alors de déterminer l’écoulement \(Q\) si l’hypothèse de considérer \(\Delta S\) négligeable est valide. Le choix de déterminer des moyennes des flux sur un temps long permet en général de garantir la validité de cette hypothèse.

Pour cette étape, il faudra donc au préalable moyenner les données de \(P\), \(ETP\) et \(Q\) sur des périodes de 10 ans, puis évaluer quels modèles de bilan permet de se rapprocher de l’écoulement observé.

L’équation de Budyko (1974) est largement utilisé dans la littérature :

\(\frac{ET}{P} = \big(\ \frac{ETP}{P} \cdot tanh \big(\frac{P}{ETP} \big)\ \cdot \big( 1 - exp \big(\ - \frac{ETP}{P} \big) \big)^{0.5}\)

Des alternatives existent cependant à cette équation, comme les formules de Schreiber, Turc-Mezentsez, Ol’Dekop ou Fu-Tixeront. le détail des équations des ces formules sont données ici :

Schreiber (1904) : \(\frac{ET}{P} = 1 - exp \big(\ -\frac{ETP}{P} \big)\)
Ol’Dekop (1911) : \(\frac{ET}{P} = \frac{ETP}{P} \cdot tanh \big(\frac{P}{ETP} \big)\)
Tixeront(1964) et Fu (1981) : \(\frac{ET}{P} = 1 + \frac{ETP}{P} - \big(1 + \frac{ETP}{P} \big)^{0.5}\)

Plusieurs auteurs ont également suggéré de rajouter un degré de liberté à ces équations afin de rendre l’estimation plus proche de l’observation. On peut citer :

L’approche paramétrique de Schreiber : \(\frac{ET}{P} = 1 - exp \big(\ - \alpha \cdot \frac{ETP}{P} \big)\)
L’approche paramétrique de Tixeront-Fu : \(\frac{ET}{P} = 1 + \frac{ETP}{P} - \big(1 + \frac{ETP}{P} \big)^{\frac{1}{\omega}}\)

8.2.3.3 Etape 2 : Vérifiez que les simulations climatiques historiques ne sont pas biaisées

Les données de simulations de modèles de climat mises à disposition pour cette étude de cas sont des données dites débiaisées. C’est-à-dire que les sorties “brutes” des modèles de climat ont été corrigées afin de s’approcher au mieux des observations. Il peut cependant subsister des écarts que vous allez évaluer dans cette étape.

Pour ces comparaisons, il est extrêmement important de bien comprendre que ces simulations sont des simulations climatiques et non des reconstitutions météorologiques. De ce fait, une simulation sur la période dite historique n’a pas pour objectif de reconstituer la temporalite des évènements climatiques mais plutôt de reconstituer le climat observé en terme fréquentiel. En d’autres termes, il n’est pas pertinent de comparer les pluies observées et simulées pour l’année a. En revanche, comparer les moyennes (et/ou des quantiles) et écart-types des pluies sur toute la période historique est pertinent.

8.2.3.4 Etape 3 : Analysez les projections climatiques sur votre bassin versant

En général, ces analyses se font en analysant le climat sur des périodes suffisamment longues (afin de gommer l’effet de la variabilité naturelle du climat). Vous pourrez choisir par exemple deux échéances : la période 2041-2070 et la période 2071-2100, à comparer avec la période historique (par exemple 1976-2005).

Il est important de bien spécifier quelles périodes vous utilisez lorsque vous présentez vos résultats, notamment la période historique. Selon les rapports du GIEC, cette période peut être la période actuelle (e.g. 1961-1990 ou 1981-2010) ou la période pré-industrielle (e.g. 1850-1900).

Comme pour l’étape 2, vous pouvez analyser les variations de moyennes, de quantile ou d’écart-types, en fonction de si vous voulez caractériser le changement moyen, le changement sur les extrêmes ou le changement en terme de variabilité. D’une façon générale, ces variations et l’écart des variations d’une projection climatique à une autre s’analyse en relatif, i.e. si vous étudier le modèle i, vous allez comparer les simulations de ce modèle i sur la période de référence et sur une période du futur. Ceci est préférable que de comparer les observations avec les simulations sur les périodes futures, car les simulations sur les périodes historiques peuvent comporter des biais. Les changements se calculent généralement en relatif pour les précipitation et les évapotranspirations potentielles et en absolu pour les températures.

N’hésitez pas à comparer vos résultats à ceux des rapports AR5 et AR6 du GIEC. Vous pouvez aussi visiter l’atlas interactif du GIEC https://interactive-atlas.ipcc.ch

8.2.3.5 Etape 4 : Estimez les écoulements futurs de votre bassin versant

Il suffit dans cette section d’appliquer le modèle que vous avez choisi en utilisant les projections climatiques disponibles.

8.3 Modélisation des crues

Cette activité mobilise les notions vues dans la section “Écoulement”. Les acquis d’apprentissage visés sont :

S’initier à la modélisation hydrologique
Estimer les paramètres des fonctions de production et de transfert à partir de données observées de pluie et de débit
Suggérer des ajustements des méthodes ou des paramètres pour améliorer les simulations produites

8.3.1 Contexte de l’étude de cas proposée

La modélisation hydrologique est aujourd’hui au cœur de l’hydrologie scientifique. Même si la modélisation n’a pas été abordée de façon explicite dans les cours de ce module, les notions vues dans la section “Écoulement” vont vous permettre de vous initier à la modélisation.

L’étude proposée ici est assez proche des analyses qui peuvent être menées en bureaux d’études, lorsque l’on cherche à déterminer un “débit de projet” afin de dimensionner les différents ouvrages hydrauliques. L’estimation de ce débit requiert la détermination d’une pluie de projet, d’une répartition temporelle de la pluie nette (fonction de production), ainsi que d’une fonction de transfert permettant de transformer la pluie nette en hydrogramme.

Une partie de l’analyse repose sur la sélection d’évènements de crue et la séparation entre écoulement rapide et lent. Ces étapes sont longues et délicates et les évènements sélectionnés ainsi que la séparation des hydrogrammes sont des données fournies, que vous remettrez éventuellement en question.

8.3.2 Méthodologie et données

Cette section détaille les données que vous pouvez utiliser et les méthodes à suivre.

8.3.2.1 Etapes de l’étude de cas

Vous pourrez suivre la démarche suivante :

Mise en place de la stratégie de calage-validation.
Détermination du/des paramètres de la fonction de production
Détermination du/des paramètres de la fonction de transfert
Application du modèle sur les évènements de validation

Ces différentes étapes marqueront les différentes taches à réaliser pour cette étude de cas.

8.3.2.2 Données mobilisées pour l’étude de cas

Toutes les données utilisées dans le cadre de cette étude de cas sont publiques. Ces données publiques sont disponibles sur d’autres bassins à l’échelle de la France et la méthodologie est donc réplicable à d’autres bassins versants. Les données historiques d’observation de précipitation de bassin et de débit sont extraites de la base de données CAMELS-FR (https://doi.org/10.57745/WH7FJR).

En général, on dispose des données historiques sur près de 50 ans (1971-2020) de données en continu au pas de temps journalier. Dans cette étude de cas, le travail se focalise sur la modélisation à l’échelle des évènements. Nous avons donc réalisé en amont de cette étude une sélection d’évènements de crue à partir des chroniques journalières continues. Cette étape de séparations des évènements a suivi la méthodologie décrite dans Saadi et al. (2020).

Dans l’outil de visualisation des données proposé ci-dessous vous permettra de choisir le bassin versant d’étude en connaissance de sa situation géographique et des caractéristiques topographique et d’occupation du sol. Il vous permettra aussi de visualiser les évènements et d’en importer les données.

Les données d’altitude ont été extraites du produit SRTM et les donnes d’occupation du sol du produit Corine Land Cover. Ces deux bases de données sont en accès libre. L’outil de visualisation de données a été développé avec le package R Shiny. Pour un rendu optimal, ouvrez dans un nouvel onglet en cliquant ici

8.3.3 A vous de jouer…

8.3.3.1 Etape 0 : Choisissez votre bassin versant et charger les données nécessaires

Vous avez le choix entre 11 bassins versants situés dans différents contextes climatique et géographique. L’outil de visualisation des données vous permettra de charger les données nécessaires.

8.3.3.2 Etape 1 : Déterminez les pluies de bassin à partir de méthodes de spatialisation

Cette étape est importante et doit se faire de façon indépendante des autres étapes. C’est-à-dire que vous ne devez pas revenir sur le choix des évènements une fois que le travail de calage des paramètres est initié.

Le travail ici consiste à composer deux sous ensemble d’évènements : un ensemble de calage qui servira à déterminer les paramètres du modèle et un ensemble de validation qui servira à tester le modèle dans des conditions opérationnelles. Voici quelques éléments à considérer pour vous guider dans votre choix

Vous pouvez commencer par analyser les évènements disponibles en fonction des saisons d’occurrence ;
Vous pouvez distinguer des évènements “simple” générer par une pluie continue ou des évènements multiples générés par plusieurs évènements pluvieux. Il peut être plus facile de déterminer les paramètres de la fonction de transfert lorsque le débit est généré par une seule pluie nette sur un pas de temps. Des évènements simples doivent donc constituer votre ensemble de calage ;

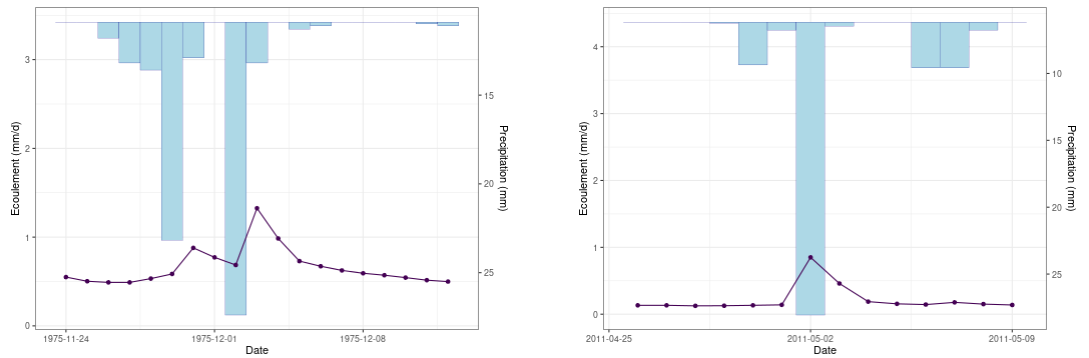
deux hydrogrammes

Exemple de deux hydrogrammes. A gauche, un écoulement complexe lié à deux évènements de pluie rapprochés mais avec une interruption et à droite une crue généré par une seule grosse pluie sur un pas de temps.

Vous pouvez distinguer les évènements en fonction du cumul d’écoulement de surface “Quickflow” et du rapport entre ce cumul et le cumul de pluie de l’évènement.

8.3.3.3 Etape 2 : Détermination du/des paramètres de la fonction de production

La fonction de production va permettre de déterminer la pluie nette, c’est-à-dire la part de la pluie brute qui va être convertie en écoulement de surface (“quickflow”). Plusieurs fonctions de production ont été présentées dans la section Écoulement du cours.

Nous proposons ici (mais vous êtes libres de faire un autre choix) de tester la méthode SCS (Soil Conservation Service) et de faire l’hypothèse d’un « Curve Number » CN unique quel que soit le degré de saturation du sol (les évènements ont été sélectionnés de telle sorte que les précipitations antérieures étaient faibles).

Vous utiliserez les données des évènements de votre ensemble de calage pour ajuster CN au bassin versant. L’hypothèse principale de la méthode SCS (Soil Conservation Service) est que le rapport des pertes réelles sur les quantités d’eau ruisselées est égal au rapport des pertes maximales potentielles sur le ruissellement maximum potentiel. Ceci peut s’écrire simplement comme suit :

\[ \sum_{j=1}^{nbj} Pn_j = \frac{(\sum_{j=1}^{nbj} P_j-I_a)^2}{\sum_{j=1}^{nbj} P_j-I_a + S} \quad (1) \]

où \(Pn_j\) est la pluie nette du jour \(j\), \(nbj\) est le nombre de jours de l’évènement, \(P_j\) est la pluie de jour \(j\), \(I_a\) est l’abstraction initiale et \(S\) est la capacité de stockage du bassin versant.

Pour réduire le nombre de paramètre, nous utiliserons l’hypothèse classique reliant S au curve number \(CN\) (équation 2) et la relation entre l’abstraction initiale et la capacité de stockage du bassin versant (équation 3).

\[ S = 25.4(\frac{1000}{CN} -10) \quad (2) \]

\[ I_a = 0,2.S \quad (3) \]

Ainsi, l’équation (1) devient :

\[ \sum_{j=1}^{nbj} Pn_j = \frac{(\sum_{j=1}^{nbj} P_j - 0,2.S)^2}{\sum_{j=1}^{nbj} P_j + 0,8.S} \quad (4) \]

avec :

\[ S = 25.4(\frac{1000}{CN} -10) \quad (5) \]

Pour chaque évènement, vous connaissez l’écoulement de surface “Quickflow” et par définition, le cumul de pluie nette sur l’évènement est égal au cumul d’écoulement de surface :

\[ \sum_{j=1}^{nbj} Pn_j = \sum_{j=1}^{nbj} Qs_j\quad (6) \]

Il est donc possible de déterminer la valeur de CN pour chaque évènement.

Ces valeurs de CN pourront être discutées vis-à-vis des valeurs de CN tabulaires que l’on peut mobiliser lorsqu’aucune donnée de débit n’est disponible (voir tableau ci-dessous).

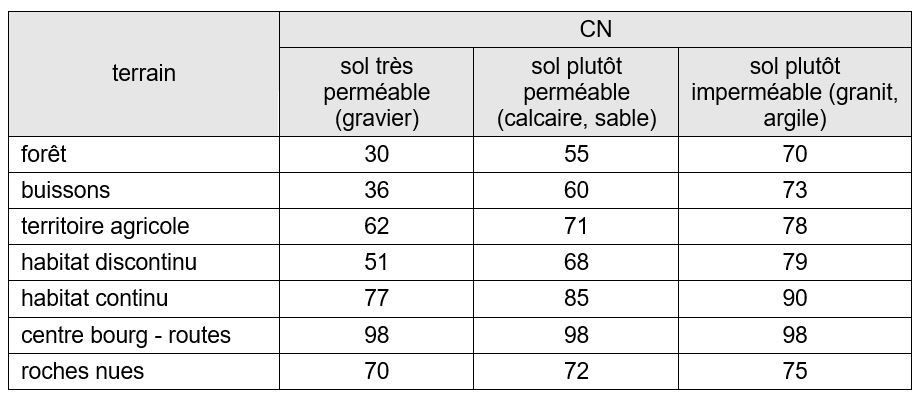
Valeurs references de CN

8.3.3.4 Etape 3 : Détermination du/des paramètres de la fonction de transfert

Vous déterminerez l’hydrogramme unitaire à partir d’une sélection d’évènements « simples », c’est-à-dire d’évènements de crue générés par une pluie nette concentrée sur un seul jour.

Le cheminement pour déterminer les ordonnées de l’hydrogramme unitaire est le suivant :

Recensement des évènements pluie-débits passés, en se focalisant sur les évènements avec une seule pluie nette (vous avez besoin ici de la fonction de production déterminée à l’étape 2)
Normalisation des hydrogrammes de chaque évènement pour que la somme des écoulements de surface soit égale à 1.
Détermination d’un hydrogramme “moyen” à partir de l’ensemble des hydrogrammes normalisés.

8.3.3.5 Etape 4 : Application du modèle sur les évènements de validation

Cette étape consiste à appliquer le modèle obtenu (fonction de production + fonction de transfert) sur les évènements de validation. Plusieurs critères peuvent être ensuite considérés pour juger la qualité du modèle (en termes de respect des volumes, de respect des dynamiques). Des critères numériques comme le critère de Nash et Sutcliffe (1970) ou le critère de Kling- Gupta sont assez répandus et permettront de qualifier la qualité du modèle obtenu.

Pour aller plus loin, on pourra imaginer des tests de sensibilité du modèle au choix des paramètres (CN et ordonnées de l’hydrogramme unitaire), soit en faisant varier les valeurs des paramètres autour des valeurs déterminées aux étapes 1 et 2. Pour le CN, on peut aussi le faire varier pour quantifier l’impact de changements d’occupation du sol par exemple.

8.4 Abattement spatial et temporel des précipitations

Cette activité mobilise les notions vues dans les sections “Précipitations” et “Outils statistiques de l’hydrologie”. Les acquis d’apprentissage visés sont :

Appliquer les méthodes de détermination des extrêmes hydrologiques (ici les pluies décennales) ;
Comprendre le phénomène d’abattement des précipitations et les implications de cet abattement pour les calculs d’hydrologie opérationnelle ;
Suggérer des explications des résultats trouvés et les comparer avec les résultats de la littérature

8.4.1 Contexte de l’étude de cas proposée

Pour la majorité des applications hydrologiques, l’étendue du bassin versant n’est pas suffisamment petite pour que la pluie de bassin puisse être supposée égale à une pluie ponctuelle de projet estimée par ailleurs.

En effet, les lames précipitées moyennes maximales affectant une surface donnée décroissent, toutes choses étant égales par ailleurs, avec la superficie de cette surfaces (Hingray et al., 2009). On parle alors d’abattement spatial. Ceci peut se concevoir assez simplement lorsque l’on regarde une animation radar de précipitation : les cellules pluvieuses peuvent être plus petites que le bassin versant et elles se déplacent dans l’espace (voir l’animation ci-dessous) :

De même, il est souvent utile de déterminer une intensité de pluie de projet sur une durée caractéristique de réponse du bassin versant et cette durée n’est pas forcément identique au pas de temps de la donnée de précipitation. Pour les mêmes raisons que précédemment, à savoir que les précipitations ne sont pas maximales au même moment sur l’ensemble du bassin versant, l’intensité maximale d’une pluie de projet diminue avec l’augmentation de la durée de l’évènement et on parle alors d’abattement temporel.

L’objectif de ce projet est de caractériser ces abattements spatial et temporel empiriquement sur une base de données de précipitations. Cette question est centrale en hydrologie

8.4.2 Méthodologie et données

Cette section détaille les données que vous pouvez utiliser et les méthodes à suivre.

8.4.2.1 Etapes de l’étude de cas

Vous pourrez suivre la démarche suivante :

Détermination des pluies décennales à en testant plusieurs configuration de moyennage spatial et temporel ;
Détermination des coefficients d’abattement respectifs ;
Comparaison aux résultats d’études similaires.

Ces différentes étapes marqueront les différentes taches à réaliser pour cette étude de cas.

8.4.2.2 Données mobilisées pour l’étude de cas

Vous pouvez choisir un des quatre postes pluviométriques ci-dessous. Ces postes on été choisis car ils présentent des climatologies sont variées et un relief alentour peu marqué.

Pour chaque poste, vous avez à disposition les données de précipitation horaire au niveau du poste (source MétéoFrance, https://www.data.gouv.fr/fr/datasets/donnees-climatologiques-de-base-horaires/) sur la période 2000-2019. Il peut y avoir quelques données lacunaires, qui sont marquées par des NA dans les fichiers de données. Ces données lacunaires étant peu nombreuses, on considérera que cela ne biaise pas l’analyse et la détection des valeurs maximales de chaque année.

En plus des données au niveau du poste pluviométrique, vous trouverez das les fichiers de données les données radars de la base de données Comephore (COmbinaison en vue de la Meilleure Estimation de la Précipitation HOraiRE), qui est une réanalyse horaire des précipitations par fusion des données des radars et des pluviomètres, couvrant la France métropolitaine. es données sont en accès publique (https://www.data.gouv.fr/fr/datasets/reanalyses-comephore/) au format Netcdf d’une résolution spatiale de 1km² et d’une résolution temporelle horaire. Le traitement spatial de ces données a déjà été réalisé et vous avez à disposition des chroniques horaires de précipitations de 2000 à 2019 sur le pixel (de 1km²) contenant le poste pluviométrique, puis sur des disques de rayons de 5, 10, 15, 20 et 25 km.

Accès aux fichiers de données :


Poste d’Amberieu (01)	Poste de Brive (19)
Poste de St Martial Viveyrols (24)	Poste d’Orléans (45)

8.4.3 A vous de jouer…

8.4.3.1 Etape 0 : Choisissez votre station et charger les données nécessaires

Vous avez le choix entre 4 pluviomètres situés dans différents contextes climatique et géographique. L’outil de visualisation des données vous permettra de discuter des contextes climatiques et surtout topographiques. Les analyses proposées font l’hypothèse implicite d’une isotropie des précipitations, hypothèse qui n’est pas forcément vérifiée si on a de forts gradients topographiques.

8.4.3.2 Etape 1 : Détermination des pluies décennales en moyennant spatialement et temporellement

Cette étape consiste à déterminer les pluies décennales pour différentes agrégations spatiales et temporelles. Pour la détermination des coefficients d’abattement, on considérera la pluie de référence comme étant la pluie décennale déterminée avec les données de la station pluviométrique au pas de temps horaire.

Cette pluie décennale de référence sera comparée aux pluies décennales obtenus sur le pixel de la station (1km²) puis en agrégeant spatialement les pixels autour de la station pluviométriques pour des disques de rayons de 5, 10, 15, 20 et 25 km.

On comparera aussi la pluie de référence à la pluie décennale obtenue en moyennant temporellement les intensités sur 3, 6, 12 et 24h.

La détermination de la pluie décennale se fait par ajustement d’une loi de Gumbel sur les précipitations maximales annuelles. L’identification des maxima annuels peut se faire sur un tableur (avec par exemple un tableau croisé dynamique) ou par un script sur un langage de programmation. Par exemple, si on utilise R, on pourra utiliser la fonction aggregate.

A partir des valeurs maximales annuelles, il s’agit ensuite de déterminer les deux paramètres \(\lambda\) et \(\beta\) de la loi de Gumbel associée (voir le TD et son corrigé).

8.4.3.3 Etape 2 : Détermination des coefficients d’abattement

Une fois les pluies décennales calculée, le coefficient d’abattement s’obtient en divisant la pluie décennale de chaque configuration d’agrégation à la pluie de référence :

\[K = \frac{P_m}{P_{ref}}\]

où \({P_{ref}}\) est la pluie décennale de référence (au niveau de la station pluviométrique et au pas de temps horaire) et \(P_m\) la pluie décennale en ayant moyennené au préalable des intensité spatialement ou temporellement.

8.4.3.4 Etape 3 : Comparaison aux résultats d’études similaires

Dans cette partie, vous comparerez les abattements spatiaux et temporels aux résultats de la littérature.

On pourra par exemple comparer les résultats avec ceux de Neppel et al. (2003), notamment la Figure 3, reproduite ci-dessous :

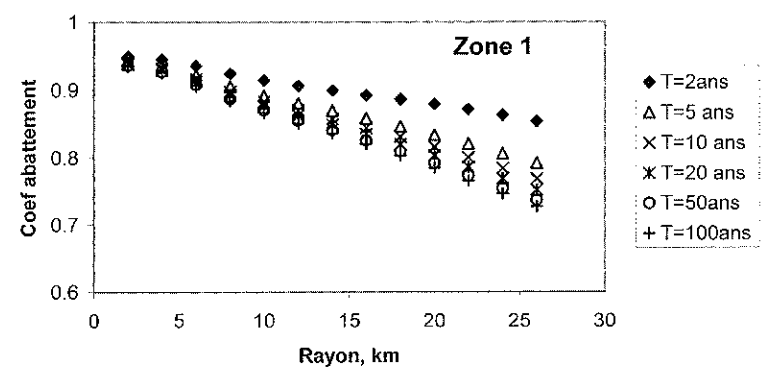
Abattement Neppek 2003

Relation coefficient d’abattement et surface (Neppel et al. 2003)

Cet article présente aussi des formulations de l’abattement en fonction de la surface considérée, formule que l’on pourra déployer pour les données du poste choisi.

L’article de Panthou et al. (2015) présente aussi des résultats expérimentaux à différents niveaux d’agrégation spatiaux et temporels, notamment la Figure 6, reproduite ci-dessous.

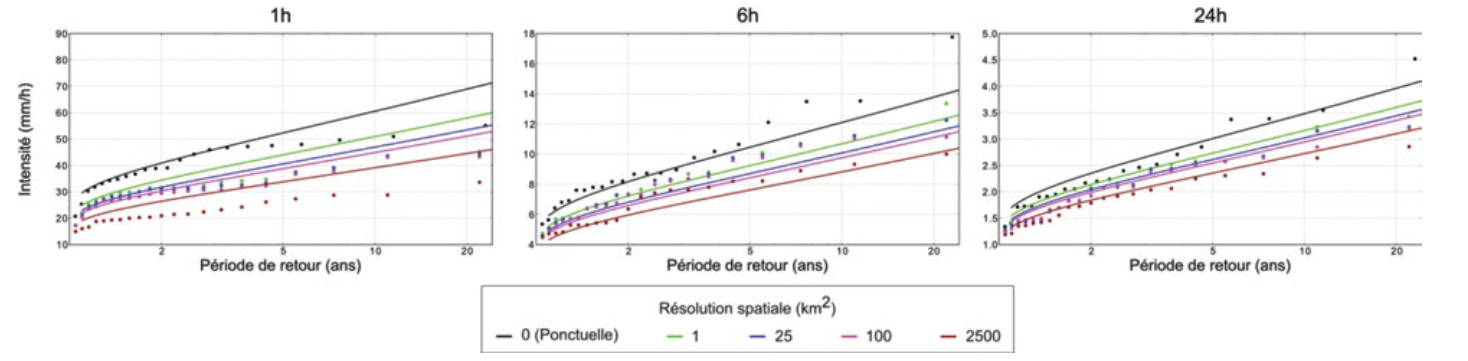
Abattement Neppel 2003

Relation coefficient d’abattement surface et durée (Panthou et al. 2015)

A vous de voir comment faire pour comparer au mieux vos résultats avec ceux de la littérature, en refaisant des calculs si nécessaire et en allant chercher d’autres références bibliographiques !