Chapter 10 Monte Carlo Experiments

Definition 10.1 Monte Carlo Simulations are a class of computational algorithms that rely on repeated random sampling to estimate numerical results.

They are widely used in various fields, including statistics, physics, finance, and machine learning, to approximate complex mathematical problems that may not have closed-form solutions.

A Monte Carlo Simulation or Experiment is also useful in evaluating the impact of certain conditions (non-normality, model misspecification etc.) on statistical methods (about estimation, prediction etc.) based on some score (MSE, Bias, MAPE etc.)

Monte Carlo Simulation is just a computer EXPERIMENT

For our class, the following is the proposed outline for creating a Monte Carlo Experiment

  1. Set up scenarios (design space)

    • Define your objective (what question to answer).

    • Choose key factors and reasonable levels.

    • Specify the data-generating process for each scenario.

  2. Select performance metrics (score function)

    • Pick measures tied to the objective (bias, MSE, SE, power, coverage, accuracy, etc.).

    • Decide how results will be summarized (averages, MC-SE, plots).

    • Include a diagnostic check (e.g., type I error when null is true).

  3. Identify comparison methods

    • Establish a baseline (control), usually the most common methodology used

    • Add alternative(s) for evaluation.

    • Fix parameters/settings in advance.

  4. Summarize

Monte Carlo methods can be applied to estimate parameters of the sampling distribution of a statistic, mean squared error (MSE), percentiles, or other quantities of interest.

It also can be designed to assess the coverage probability for confidence intervals, to find an empirical Type I error rate of a test procedure, to estimate the power of a test, and generally, to compare the performance of different procedures for a given problem.

This chapter will help you design Monte Carlo experiments that are grounded on statistical inference.

Methods for evaluating point estimators, interval estimators, and hypothesis tests are from Casella & Berger (2002). Examples are derived from handouts of Bilon (2021) and Supranes (nd).

In a Monte Carlo experiment, we can assess the performance of an estimator by repeatedly simulating data from a known population, allowing us to approximate its sampling distribution, standard error, bias, and mean squared error.

Random variates from the sampling distribution of an estimator \(\hat{\theta}\) can be generated by repeatedly drawing independent random samples \(\textbf{x}_m\) and computing \(\hat{\theta}_m\) = \(\hat{\theta}(x_{1(m)}, . . . , x_{n(m)})\) for each sample.

10.1 Sampling Distribution of a Statistic

One type of problem that arises frequently in statistical applications is the need to evaluate the cdf of the sampling distribution of a statistic, when the density function of the statistic is unknown or intractable.

Recall from Section 9.2 and Theorem 9.1, the empirical cdf.

Definition 10.2 A Monte Carlo estimate of the sampling distribution of a statistic is

\[ P(\hat{\theta} \leq t)\approx F_M(t)=\frac{1}{M}\sum_{m=1}^MI(\hat{\theta}_m\leq t) \]

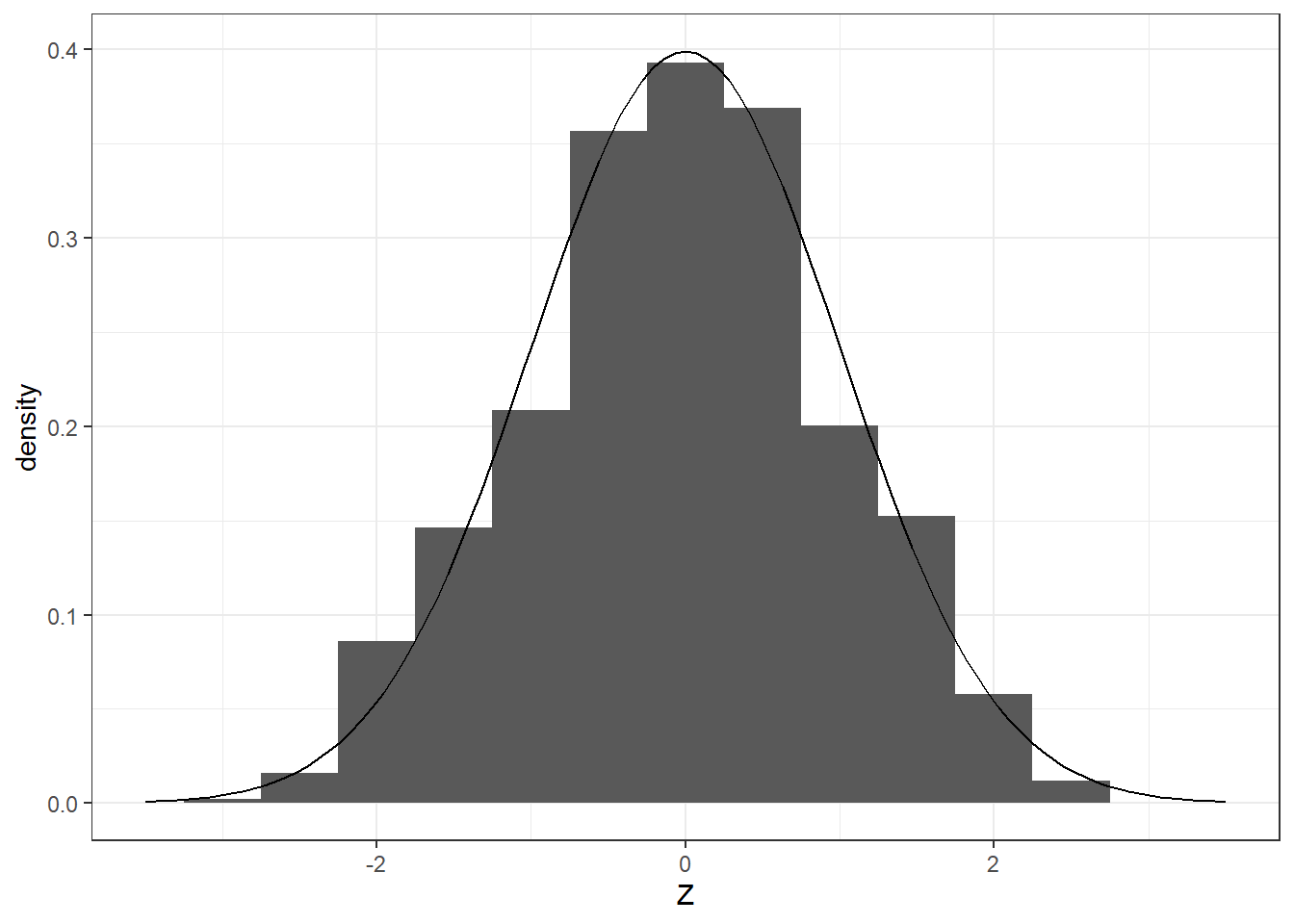
Example: Central Limit Theorem

As an example, we visualize distribution of the statistic

\[ \frac{\bar{X}_n-\mu}{\sigma/\sqrt{n}} \] By the Central limit theorem, we know that this approaches the standard normal distribution, for a random sample \(X_1,X_2,...,X_n\) from a population with mean \(\mu\) and finite variance \(\sigma^2\).

Suppose the population has a distribution \(Poisson(\lambda = 6)\). The mean and variance are both \(\lambda = 6\).

Let’s obtain a random sample of size \(n=30\) repeatedly and examine the distribution of the statistic \(\frac{\bar{X}-\mu}{\sigma/\sqrt{n}}\).

Here, we use the replicate function. This is a faster way than using loops when conditions are the same each iteration and the goal is to generate a vector.

M <- 1000
n <- 30
Z <- replicate(M, 
               {X <- rpois(n, lambda = 6)
               (mean(X) - 6)/sqrt(6/n)
               })

It looks standard normal, doesn’t it?

Suppose we obtained the following sample from the population:

set.seed(142)
samp <- rpois(n, lambda = 6)

Computing \(\frac{\bar{X}-\mu}{\sigma/\sqrt{n}}\) using this sample, wehave:

z <- (mean(samp) - 6)/sqrt(6/n)
z
## [1] 1.565248

By the central limit theorem, \(P(Z \leq 1.57)\approx \Phi(1.57)=0.9412\)

pnorm(z)
## [1] 0.9412376

But using Monte-Carlo Simulation, we count how many samples will have a Z-statistic that are less than the observed Z-statistic

sum(Z <= z)/M
## [1] 0.938

Close enough?

This Monte Carlo approach is more useful if the probability distribution of a statistic has no closed form, or has no theorem that support convergence in distribution. Try to explore the distribution of other statistics, like the statistics used in non-parametric inference (e.g. Wilcoxon Signed-Rank Statistic, Wilcoxon Rank-Sum / Mann–Whitney U Statistic, Kruskal–Wallis H Statistic, Spearman’s Rank Correlation Coefficient, Kendall’s Tau, etc…)

10.2 Monte Carlo Methods for Evaluating Estimators

Inferential statistics draws conclusions about a population based on an estimator that can be computed using a sample. Recall that a parameter can have different estimators, and a difficulty that arises when we are faced with the task of choosing between estimators.

Bias of a point estimator

Recall that the bias of an estimator \(\hat{\theta}\) of a parameter \(\theta\) is the difference between the expected value of \(\hat{\theta}\) and \(\theta\); that is, \(Bias_\theta(\hat{\theta})=\mathbb{E}(\hat{\theta})-\theta\). It is difficult to obtain the bias if you don’t know the expectation of an estimator.

By law of large numbers, if you have \(M\) replicates of \(\hat{\theta}\), then \(\frac{1}{M}\sum_{m=1}^M \hat{\theta}_m\rightarrow\mathbb{E}(\hat{\theta})\)

Definition 10.3 A Monte Carlo estimate for the bias of an estimator \(\hat{\theta}\) in estimating \(\theta\) is

\[ \widehat{Bias}_\theta(\hat{\theta})=\frac{1}{M}\sum_{m=1}^M \hat{\theta}_m-\theta \]

Example

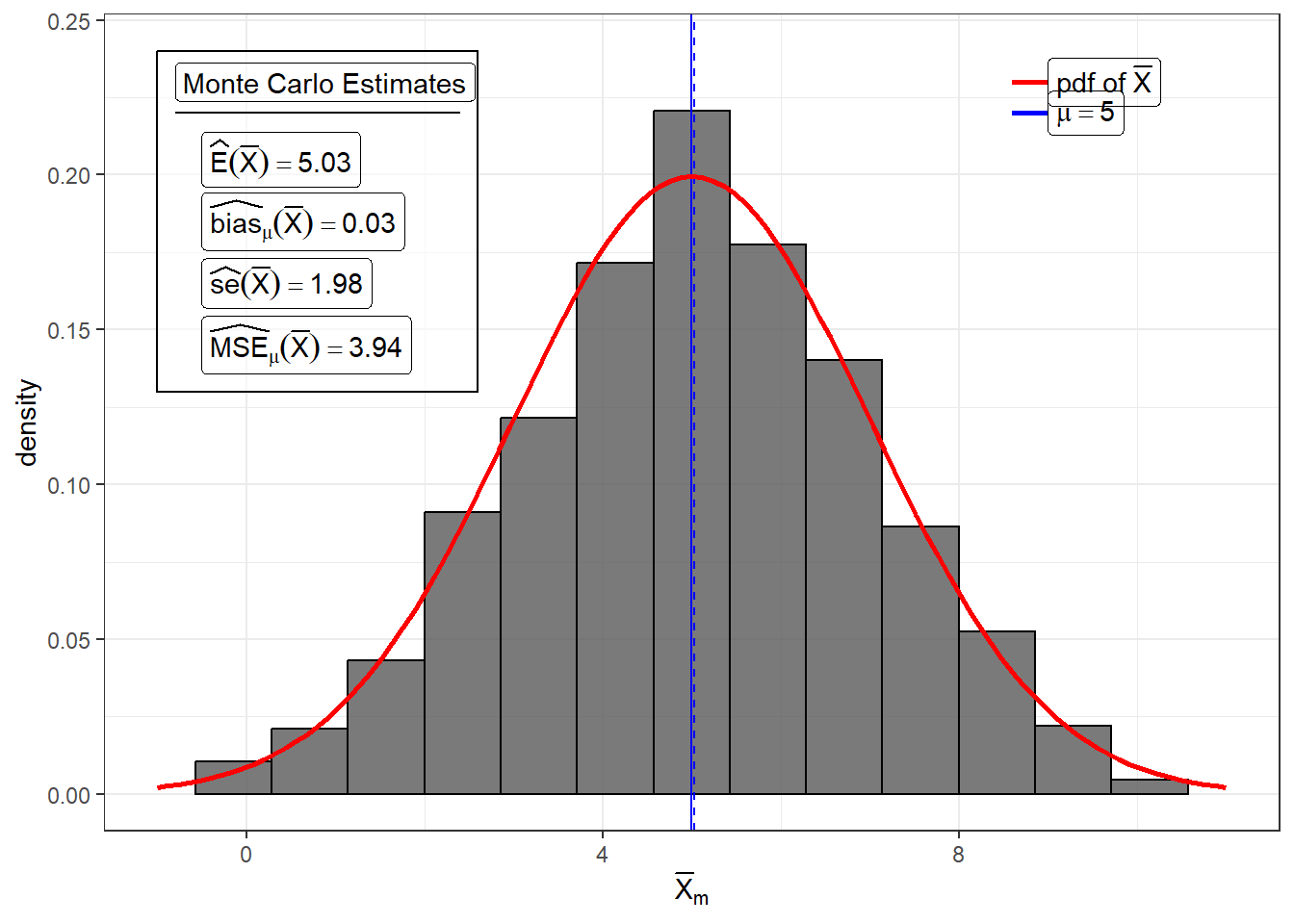
For example, we know that the the sample mean \(\bar{X}\) is unbiased for \(\mu\). Suppose \(X_1,...,X_{25}\sim N(\mu = 5, \sigma^2 = 100)\), then \(Bias_\mu(\bar{X})=0\).

set.seed(142)
M <- 1000
xbar <- replicate(M, mean(rnorm(25, mean = 5, sd = 10)))
bias_xbar <- mean(xbar) - 5
bias_xbar
## [1] 0.03515856

Standard Error of a Statistic

Suppose \(\hat{\theta}\) is an estimator of \(\theta\). We can obtain a Monte Carlo estimate of its standard error by obtaining \(M\) samples of this statistic.

Definition 10.4 A Monte Carlo estimate for the variance of a statistic \(\hat{\theta}\)

\[ \widehat{Var}(\hat{\theta}) =\frac{1}{M}\sum_{m=1}^M(\hat{\theta}_m-\bar{\hat{\theta}})^2 \] and a Monte Carlo estimate for the standard error of a statistic \(\hat{\theta}\)

\[ \widehat{se}(\hat{\theta}) = \sqrt{\frac{1}{M}\sum_{m=1}^M(\hat{\theta}_m-\bar{\hat{\theta}})^2} \] where \(\bar{\hat{\theta}}\) is the sample mean of the \(\hat{\theta}_m\)s

Note: You may use \(M\) or \(M-1\) in the denominator.

In other words, you may use the formula for the sample variance and sample standard deviation. Difference will be negligible anyway for large \(M\)*

Example

For example, we know that the standard error of the sample mean \(\bar{X}\) is \(\sigma/\sqrt{n}\). Suppose \(X_1,...,X_{25}\sim N(\mu = 5, \sigma^2 = 100)\), then \(se(\bar{X})=2\).

set.seed(142)
M <- 1000
xbar <- replicate(M, mean(rnorm(25, mean = 5, sd = 10)))
var_xbar <- mean((xbar-mean(xbar))^2)
var_xbar
## [1] 3.940161
se_xbar <- sqrt(var_xbar)
se_xbar
## [1] 1.984984

MSE of a point estimator

Recall that the mean square error (MSE) of an estimator \(\hat{\theta}\) of a parameter \(\theta\) is defined by \(\mathbb{E}(\hat{\theta}-\theta)^2\)

Monte Carlo methods can be applied to estimate the MSE of an estimator.

Definition 10.5 A Monte Carlo estimate of the \(MSE\) of an estimator \(\hat{\theta}\) of parameter \(\theta\) is

\[ \widehat{MSE}_\theta(\hat{\theta}) = \frac{1}{M}\sum_{m=1}^M(\hat{\theta}_m-\theta)^2 \]

where \(\hat{\theta}_m\) is the estimate obtained using the \(m^{th}\) random sample \(\{x_1,...,x_n\}_m\)

Example

Following the same example for \(\bar{X}\)

set.seed(142)
M <- 1000
xbar <- replicate(M, mean(rnorm(25, mean = 5, sd = 10)))
mse_xbar <- mean((xbar-5)^2)
mse_xbar
## [1] 3.941397
Decomposition of MSE

Note: the MSE can be decomposed as the sum of the variance and square of the bias

\[ \mathbb{E}_\theta(\hat{\theta}-\theta)^2 = Var(\hat{\theta}) + Bias_\theta(\hat{\theta})^2 \]

The empirical results of the simulation proves this.

var_xbar + bias_xbar^2
## [1] 3.941397
mse_xbar
## [1] 3.941397

This only works if you use the same seed number and simulation settings for the computation of the Monte Carlo estimates of Variance, Bias, and MSE.

Exercise

  1. Suppose we want to investigate the distribution of sample standard deviation (SD) of a size \(n = 200\) random sample from a \(Normal(2, 1)\).

    • Using Monte Carlo Simulation with \(M = 1000\), show the relative frequency histogram of the distribution of sample SD.

    • Based on the simulation, what is the estimated mean and variance of the distribution of sample SD?

  2. Create functions bias_mc,

Example: Mean of Poisson

Suppose our population is best modelled by a Poisson distribution (commonly used for count data). The Poisson distribution is completely described by a single parameter: rate, \(\lambda = \mu\).

The question here is

“Is the sample mean still unbiased and does it have lower variance than other estimators, say sample median?”

In this example, we will compare the bias and variance of the two estimators, sample mean and sample median in estimating the population mean for populations distributed as Poisson at different sample sizes and at different values of the parameter \(\lambda\).

  1. Obtain a sample of size \(n\) from the Poisson population.

  2. From the generated sample, compute the sample mean and sample median.

  3. Do this for \(M\) times to obtain \(M\) sample means and \(M\) sample medians.

  4. From these \(M\) values, compute the mean and variance of the sample mean and sample median so we can assess their bias and variance respectively.

See full results and source code of this example in UVLe.

10.3 Monte Carlo Methods for Evaluating Tests

When deciding whether to reject a null hypothesis \(H_0\), there is always a chance of making an error. Hypothesis tests are commonly assessed by the probabilities of these errors, such as type I and type II errors.

Suppose that we wish to test a hypothesis concerning a parameter \(\theta\) that lies in a parameter space \(\Theta\). The hypotheses of interest are

\[ H_0: \theta \in \Theta_0 \quad \text{vs} \quad H_1:\theta\in \Theta_1 \]

where \(\Theta_0\) and \(\Theta_1\) are subsets of the parameter space \(\Theta\)

Let \(\beta(\theta)\) be the probability that a test rejects \(H_0\) for a given \(\theta\).

  • If \(\theta \in \Theta_0\), then \(\beta(\theta)\) is the probability of Type I error.

  • If \(\theta \in \Theta_1\), then \(1-\beta(\theta)\) is the probability of Type II error.

In a Monte Carlo setting, we estimate these error probabilities through repeated simulation, allowing us to study how well a test controls its error rate under different scenarios. By systematically varying conditions, we can even identify tests that achieve the lowest possible error probabilities for a given situation.

Monte Carlo experiment to estimate probability of rejection for a given \(\theta\)

  1. Select a particular value of the parameter \(\theta ∈ \Theta\).

  2. For each replicate, indexed by \(m = 1, . . . , M\):

    1. Generate the \(m^{th}\) random sample \(x_1(m), . . . , x_n(m)\) under the conditions \(\theta\).

    2. Perform the test on the \(m^{th}\) sample at \(\alpha\) significance level.

    3. Record the test decision: set \(I_m = 1\) if \(H_0\) is rejected, and otherwise set \(I_m = 0\).

  3. Compute the proportion of significant tests \(\hat{\beta}(\theta) = \frac{1}{M} \sum_m^M I_m\).

\(\hat{\beta}(\theta)\) is the estimated power function. More of this will be demonstrated later.

For a good test:

  • if \(\theta \in \Theta_0\) (i.e. \(H_0\) is true), \(\hat{\beta}(\theta)\) should be close to \(0\), and the upper bound is \(\alpha\).

  • \(\hat{\beta}(\theta)\) is close to \(1\) if \(\theta \in \Theta_1\) (i.e. \(H_0\) is false)

In the following examples, we evaluate the power of the T-test for a fixed value of \(\mu\).

Suppose \(X_1, X_2, ..., X_{20}\) is a random sample from \(N(\mu,\sigma^2)\) distribution.

We have the following competing hypotheses

\[ H_0: \mu = 500 \quad \text{vs} \quad H_1:\mu >500 \] and test them at \(\alpha = 0.05\)

Empirical Type I error rate

Replicate the test procedure a large number of times under the conditions of the null hypothesis (i.e. assume \(H_0\) is true).

The empirical Type I error rate for the Monte Carlo experiment is the proportion of replicates that result to a rejection of \(H_0\).

In this simulation, we assume that the \(H_0\) is true (\(\mu=500\)). This procedure estimates \(\beta(500)\) at \(\alpha = 0.05\)

M  <- 1000
mu <- 500

pvalues <- replicate(M,{
                    #simulate under the null hypothesis
                    x <- rnorm(n, mean = mu, sd = 100) 
                    ttest <- t.test(x,alternative = "greater", mu = 500) 
                    ttest$p.value
                    }
                    )
# count how many are rejected at alpha
sum(pvalues < 0.05)/M
## [1] 0.05

In this simulation, 5% of the iterations resulted in rejection of the null hypothesis, that is, \(\hat{\beta}(500)=0.05\). This is the empirical Type I error rate.

Estimates of Type I error probability will vary, but should be close to the nominal rate \(\alpha = 0.05\) because all samples were generated under the null hypothesis from the assumed model for a t-test (normal distribution).

Empirical Type II Error Rate

Replicate the test procedure a large number of times under the alternative hypothesis (i.e. assume \(H_0\) is false).

The empirical Type II error rate \(\hat{\alpha}\) for the Monte Carlo experiment is the proportion of replicates that result to a non-rejection of \(H_0\).

In this example, we set \(\mu = 600\). This estimates \(1-\beta(\theta)\), the probability of Type II error.

set.seed(142)
M  <- 1000
mu <- 600

pvalues <- replicate(M,{
                    #simulate under the null hypothesis
                    x <- rnorm(20, mean = mu, sd = 100) 
                    ttest <- t.test(x,alternative = "greater", mu = 500) 
                    ttest$p.value
                    }
                    )

# count how many did not reject Ho  at alpha
sum(pvalues > 0.05)/1000
## [1] 0.003

In this simulation, 0.3% of the tests resulted to non-rejection of \(H_0\), given that \(H_0\) is false.

This means that at \(\alpha = 0.05\) and \(\mu = 600\), the empirical Type II error rate is 0.003.

The Power Function

Definition 10.6 The power of a test is given by the power function \(\beta(\theta)\), which is the probability of rejecting \(H_0\) for a given value of \(\theta\).

\[ \beta(\theta) = P_\theta(T\in R) = P_\theta(\text{Reject } H_0) \]

where \(T\) is the computed test statistic and \(R\) is the rejection region.

Intuitively, for a good test, \(\beta(\theta)\) should be close to 1 if \(\theta\in \Theta_1\) and close to 0 if \(\theta\in \Theta_0\)

Now, recall the errors in hypothesis test:

  1. Type I error: Reject Ho when it is in fact true

    If \(\theta\in \Theta_0\) (i.e. \(H_0\) is true), the probability of Type I error is \(\beta(\theta)\).

    \[ P_\theta(\text{Type I Error}) = P_\theta(\text{Reject } H_0) = \beta(\theta), \quad \theta\in \Theta_0 \]

  2. Type II error: Do not reject Ho when it is in fact false.

    If \(\theta\in \Theta_1\) (i.e. \(H_0\) is false), the probability of Type II error is \(1-\beta(\theta)\).

    \[\begin{align} P_\theta(\text{Type II Error}) &= P_\theta(\text{fail to Reject } H_0) \\ &= 1- P_\theta(\text{Reject } H_0), \quad \theta\in \Theta_1\\ &= 1-\beta(\theta), \quad \theta\in \Theta_1 \end{align}\]

We can use Monte Carlo Simulation to empirically evaluate the power of a test.

The goal here is to evaluate how many tests were rejected at different values of \(\theta\)

For abstraction, the following is an R function that estimates the power of T-test for a given \(\mu\).

power_T <- function(mu, mu0, M = 1000, n = 20, alpha = 0.05){
    pvalue <- replicate(M, {
                            # data generation
                            x     <- rnorm(n, mean = mu, sd = 100)
                            
                            # test
                            ttest <- t.test(x, alternative = "greater", 
                                            mu = mu0)
                            
                            # return the sequence of p values
                            ttest$p.value
                            }
                        )
    
    return(mean(pvalue<=alpha))
    
}

power_T(500, 500)
power_T(550, 500)
power_T(600, 500)
## [1] 0.046
## [1] 0.704
## [1] 0.996

Note: Since \(\Theta_0=\{500\}\) and \(\Theta = (500,\infty)\), the parameter space is \(\Theta = [500,\infty)\). We can only show the power function for values in \(\Theta\).

Now, plotting the power function at different values of \(\mu\).

set.seed(142)
theta <- seq(500, 650, by = 10)
power <- numeric(length(theta))
for(i in 1:length(theta)){
    power[i] <- power_T(theta[i], 500)
}
data.frame(theta, power) %>% 
    ggplot(aes(x = theta, y = power)) +
    geom_point(size = 3) +
    geom_line() + 
    theme_bw() +
    geom_vline(xintercept = 500, color = "red") +
    geom_hline(yintercept = 0.05, color = "red")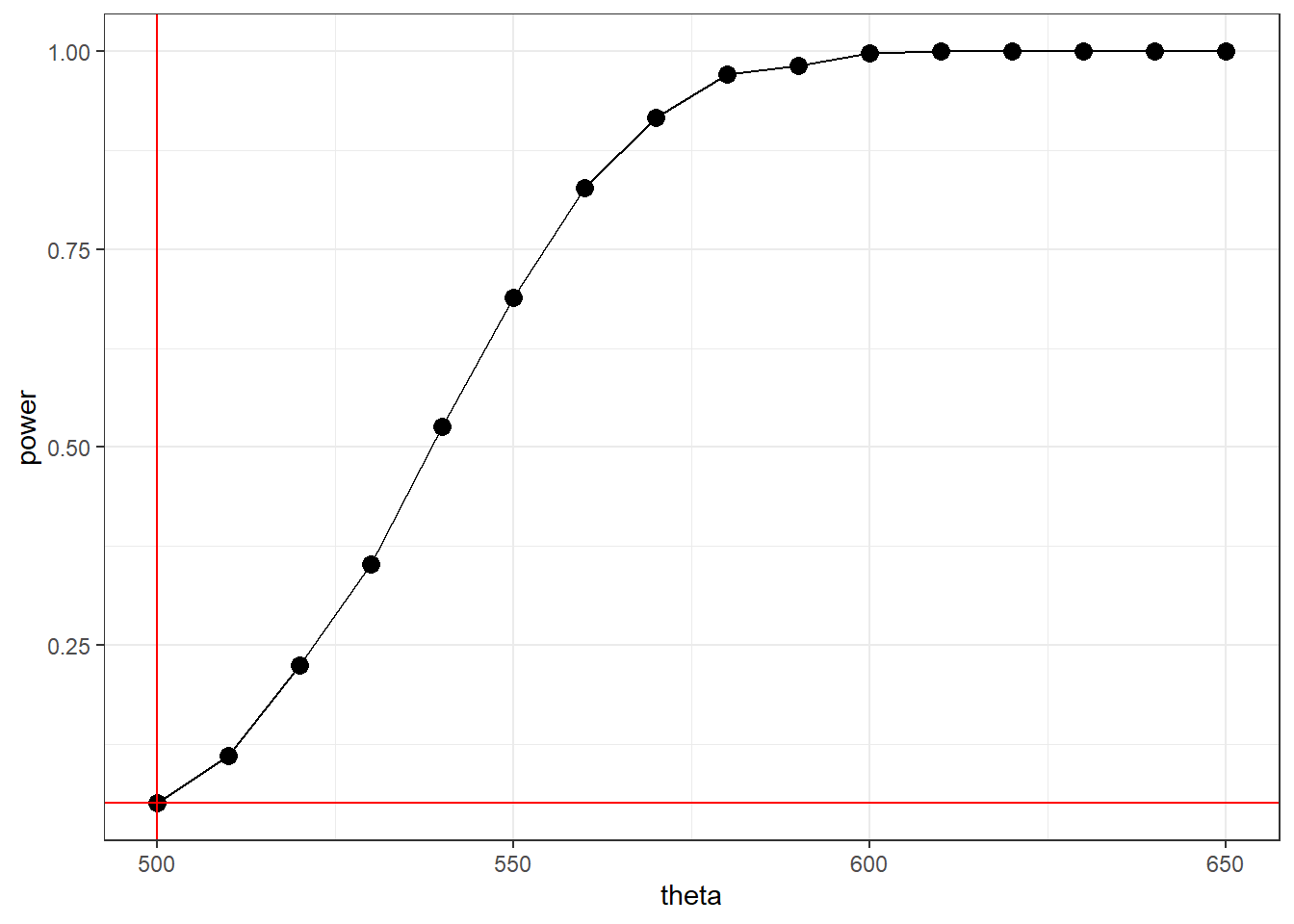

For a two-sided t-test, the power function can be defined in \(\mathbb{R}\)

power_T_2 <- function(mu, mu0 = 500, M = 1000, n = 20, alpha = 0.05){
    pvalue <- replicate(M, {
                            # data generation
                            x     <- rnorm(n, mean = mu, sd = 100)
                            
                            # test
                            ttest <- t.test(x, alternative = "two.sided", 
                                            mu = mu0)
                            
                            # return the sequence of p values
                            ttest$p.value
                            }
                        )
    
    return(mean(pvalue<=alpha))
    
}
set.seed(142)
theta <- seq(350, 650, by = 10)
power_2 <- numeric(length(theta))
for(i in 1:length(theta)){
    power_2[i] <- power_T_2(theta[i], 500, alpha = 0.05)
}
data.frame(theta, power_2) %>% 
    ggplot(aes(x = theta, y = power_2)) +
    geom_point(size = 3) +
    geom_line() + 
    theme_bw() +
    geom_vline(xintercept = 500, color = "red") +
    geom_hline(yintercept = 0.05, color = "red")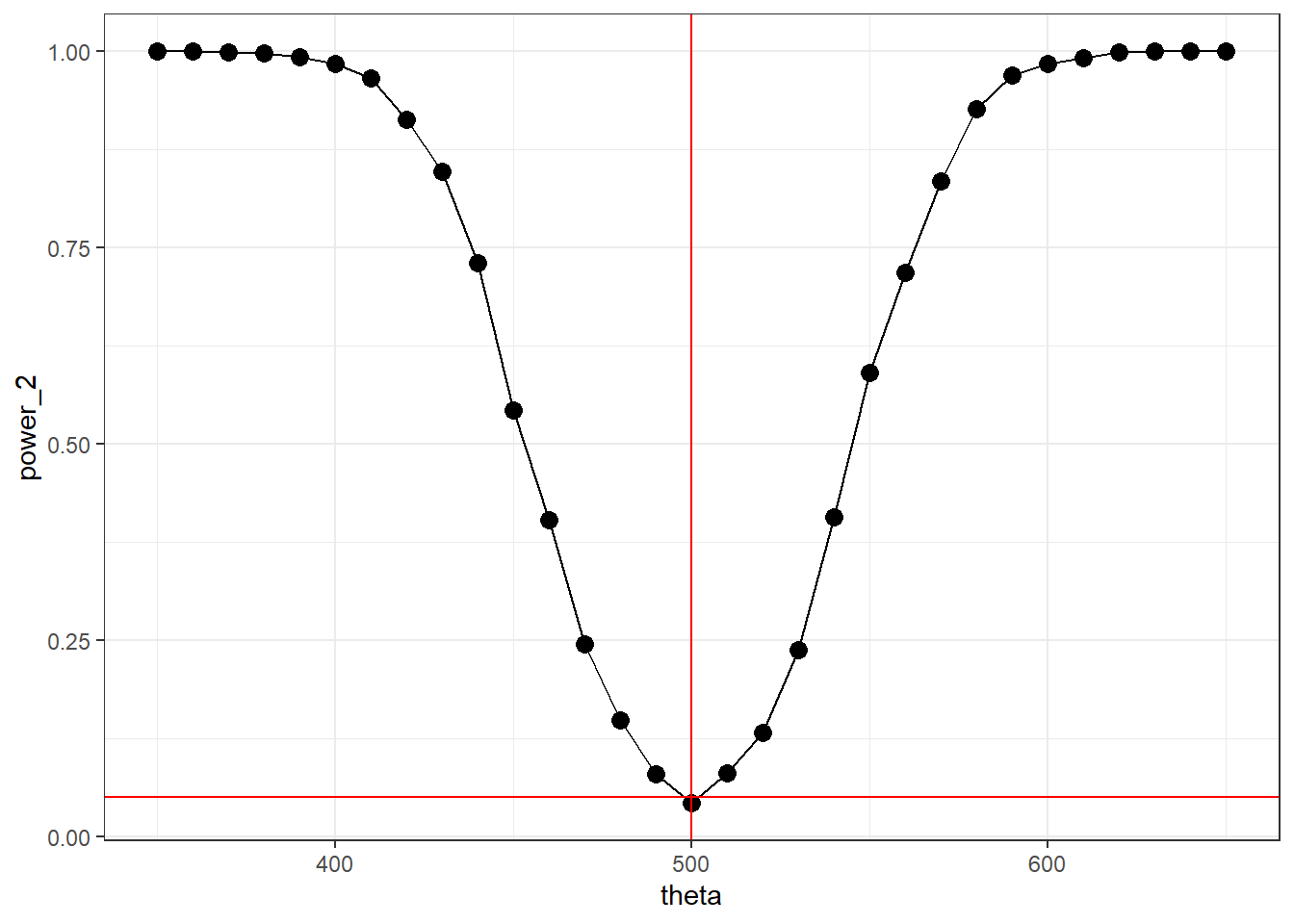

Example: Testing Mean Difference

Goal: Compare the t-test vs the Wilcoxon rank-sum test for testing the mean difference between two groups.

Simulation setup

  • Null hypothesis: two groups have the same distribution \(\mu_d = 0\).

  • Alternative: one group has a slightly shifted mean \(\mu_d\neq 0\).

  • Generate many samples under the alternative.

  • Compute the rejection rate (power) of each test.

We will consider two different scenarios:

  • Data are normally distributed (favors t-test).

  • Data are from a skewed distribution (favors Wilcoxon).

Full codes and results in UVLe.

10.4 Monte Carlo Methods for Evaluating Models

Just as Monte Carlo simulation is a powerful tool for estimating parameters and studying their properties, it is equally valuable for evaluating predictive models. In particular, we often want to understand how well a model predicts the dependent variable and to decompose its performance in terms of bias and variance.

Bias–Variance Trade-Off in Prediction

Suppose we have data \((y_i, \textbf{x}_i)\) and fit a model \(\hat{f}(\textbf{x})\) to predict \(y\). For fixed values of the predictors \(\textbf{x}\), the expected prediction error can be decomposed as

\[ \mathbb{E}[(\hat{f}(\textbf{x}) - y)^2] = \left(\text{Bias}_y[\hat{f}(\textbf{x})]\right) ^2 + \text{Var}(\hat{f}(\textbf{x})) + \sigma^2 \]

Monte Carlo Framework

A typical Monte Carlo experiment for model evaluation follows these steps:

  1. Specify a data-generating process (DGP):

\[ y_i = f(\textbf{x}_i) + \varepsilon_i \]

where \(\mathbb{E}(\varepsilon)=0\)

  1. Generate dataset that will be used as test points.

\[ y* = f(\textbf{x}^*) \]

Here, errors may be removed.

  1. Choose models to evaluate (e.g., linear regression, polynomial regression, decision trees).

  2. Repeat for \(m = 1,..,, M\)

    • Simulate a training dataset (y_{(m)}, _{(m)})

    • Fit each model to the training data

    • Predict at a grid of test points \(\textbf{x}^*\)

  3. Aggregate predictions over simulations to estimate bias and variance at each \(\textbf{x}^*\)

Exampe: OLS vs Ridge Regression

Suppose that the objective is to describe the prediction accuracy of OLS and Ridge Regression (at best tuning parameter \(k\)) in fitting a linear model under multicollinearity and misspecification.

  1. Let the data generating process be:

    \[ \textbf{y} = \textbf{X}\boldsymbol{\beta} +\boldsymbol{\varepsilon}\text{ and } cov(\boldsymbol{\varepsilon}) = \sigma^2\textbf{I} \]

    Control the number of observations and predictions to \(n=50\) and \(p=5\) respectively.

  2. The following are the factors to consider:

    Multicollinearity:

    • tolerable collinearity

    • strongly (but not perfectly) collinear independent variables

    Misspecification: what if the set of predictors cannot explain much variation in \(y\)?

    • well-specified (\(\sigma^2 = 2\))

    • lack-of-fit (\(\sigma^2 = 20\))

  3. Score for evaluation

    • Mean Absolute Prediction Error

    • Mean Squared Prediction Error

References

  • Casella, G., & Berger, R. L. (2002). Statistical inference. Brooks/Cole.

  • Rizzo, M. L. (2007). Statistical Computing with R. In Chapman and Hall/CRC eBooks. https://doi.org/10.1201/9781420010718

© 2025 Siegfred Roi L. Codia. All rights reserved.