6 Selección y Regularización
Librerías utilizadas
6.1 Selección
A pesar de su simplicidad, los modelos lineales tienen ventajas de interpretabilidad y con frecuencia muestran buen rendimiento en predicción
\[ Y = \beta_0+\beta_1X_1+\cdots+\beta_pX_p+\epsilon. \]
Esta sección aborda el cambiar el ajuste de mínimos cuadrados ordinarios (OLS) tradicional por métodos alternativos que se apalancan en OLS.
¿Por que usar alternativas a OLS?
- Predictibilidad: Si la relación entre las variables es aproximadamente lineal y si \(n\gg p\) (el número de observaciones es más grande que el número de variables), entonces OLS tiene poco sesgo y rinde bien en datos test. Sin embargo, si \(n\) no es tan grande respecto a \(p\), puede haber mucha variabilidad en OLS, lo que resulta en sobreajuste y mal rendimiento en test.
Algunos de los problemas que surgen cuando \(n\approx p\):
- Sobreajuste (Overfitting)
El error cuadrático medio (MSE) en el conjunto de entrenamiento se define como:
\[ MSE = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 \]
donde:
- \(y_i\) es el valor observado,
- \(\hat{y}_i\) es la predicción del modelo,
- \(n\) es el número de observaciones.
Cuando el número de variables \(p\) se aproxima a \(n\), el modelo puede ajustarse casi perfectamente, lo que minimiza el MSE en el conjunto de entrenamiento, pero aumenta el error en nuevos datos (error de generalización). Este es el problema del sobreajuste.
- Multicolinealidad
El problema de multicolinealidad se detecta cuando las variables explicativas están altamente correlacionadas entre sí. Un indicador común es el Factor de Inflación de la Varianza (VIF) para cada variable \(j\), que se define como:
\[ VIF_j = \frac{1}{1 - R_j^2} \]
donde \(R_j^2\) es el coeficiente de determinación de la regresión de la variable \(X_j\) sobre todas las demás variables.
Cuando \(VIF_j\) es grande (mayor a 10, por ejemplo), indica una alta colinealidad. Esto causa inestabilidad en las estimaciones de los coeficientes \(\hat{\beta}_j\), lo que puede hacer que el modelo sea sensible a pequeños cambios en los datos.
- Modelo No Identificable
En regresión lineal, los coeficientes de los parámetros \(\boldsymbol{\beta} = (\beta_1, \beta_2, \dots, \beta_p)\) se obtienen resolviendo el sistema de ecuaciones lineales:
\[ \boldsymbol{y} = \mathbf{X} \boldsymbol{\beta} + \boldsymbol{\epsilon} \]
donde:
- \(\boldsymbol{y}\) es el vector de observaciones (de dimensión \(n \times 1\)),
- \(\mathbf{X}\) es la matriz de diseño (de dimensión \(n \times p\)),
- \(\boldsymbol{\beta}\) es el vector de coeficientes,
- \(\boldsymbol{\epsilon}\) es el término de error.
Para resolver \(\boldsymbol{\beta}\), necesitamos invertir la matriz \(\mathbf{X}^T \mathbf{X}\). Si \(p \geq n\), la matriz \(\mathbf{X}^T \mathbf{X}\) no es invertible, lo que significa que el sistema es no identificable y no existe una única solución para \(\boldsymbol{\beta}\).
\[ \text{Si } \det(\mathbf{X}^T \mathbf{X}) = 0, \text{ entonces no hay solución única.} \]
- Varianza Alta
Cuando hay más variables que observaciones, el error estándar de los coeficientes de regresión se incrementa. La varianza de los coeficientes \(\hat{\beta}_j\) está dada por:
\[ \text{Var}(\hat{\beta}_j) = \sigma^2 \left( (\mathbf{X}^T \mathbf{X})^{-1} \right)_{jj} \]
donde \(\sigma^2\) es la varianza del error residual. Si \(\mathbf{X}^T \mathbf{X}\) es mal condicionada (debido a la colinealidad o alta dimensionalidad), los elementos de la matriz inversa \((\mathbf{X}^T \mathbf{X})^{-1}\) pueden ser muy grandes, lo que resulta en una varianza elevada para \(\hat{\beta}_j\). Esto significa que los coeficientes son altamente sensibles a los cambios en los datos.
- Interpretabilidad: Incluir variables independientes sin asociación con la variable dependiente en un modelo de regresión resulta en incluir complejidades innecesarias en el modelo. Si son removidas (se fijan sus coeficientes en cero), se puede obtener un modelo que es más interpretable. En OLS hay muy poca probabilidad de que se tengan coeficientes iguales a cero. Al eliminar variables estamos haciendo selección de variables o feature selection: selección de variables, contracción o regularización y reducción de dimensionalidad.
6.1.1 Selección de variables
6.1.1.1 Selección de las mejores variables
| Algoritmo: Selección de las mejores variables |
|---|
| 1. Sea \(\mathcal{M_0}\) el modelo nulo (sin predictores). Este modelo solo predice la media muestral para cada observación. |
| 2. Para \(k = 1,2,\ldots,p\): |
a. Ajusta todos \({p \choose k}\) modelos que contienen exactamente \(k\) predictores.
b. Selecciona el mejor de los \({p \choose k}\) modelos, nómbralo \(\mathcal{M_k}\). El mejor modelo se define como aquel que tiene el mejor \(RRS\) (suma de residuos al cuadrado), o de manera equivalente el más alto \(R^2\).
|
| 3. Selecciona el mejor modelo de los \(\mathcal{M_0},\ldots,\mathcal{M_k}\) usando el error de predicción en un conjunto de validación, \(C_p\), AIC, BIC o \(R^2\) ajustado. O usa el método de validación cruzada. |
Nota que este algoritmo no puede ser aplicado cuando \(p\) es grande.
También puede tener problemas de estadísticos cuando \(p\) es grande. Cuanto mayor sea el espacio de búsqueda, mayor será la posibilidad de encontrar modelos que se vean bien en los datos de entrenamiento, aunque podrían no tener ningún poder predictivo sobre datos futuros.
Por lo tanto, un espacio de búsqueda enorme puede dar lugar a un sobreajuste y a una alta varianza de las estimaciones de los coeficientes.
Por los motivos antes listado, los métodos stepwise o paso a paso son más atractivos.
\(C_p\) de Mallow
\[ C_p = \frac{1}{n}(RSS+2d\hat{\sigma}^2) \]
donde \(d\) es el total de parámetros usados y \(\hat{\sigma}^2\) es la estimación de la varianza del error \(\epsilon\).
Criterio AIC
Se puede usar en modelos donde el ajuste se realiza con máxima verosimilitud:
\[ AIC = -2\text{log}L+2d \]
Donde \(L\) es el valor máximo de la función de máxima verosimilitud del modelo.
\[ BIC = \frac{1}{n}(RSS+\text{log}(n)d\hat{\sigma}^2) \]
donde \(n\) es el número de observaciones.
\(R^2\) ajustado
\[ R^2_{adj} = 1-\frac{RSS/(n-d-1)}{TSS/(n-1)} \]
donde \(TSS\) es la suma total de cuadrados.
6.1.1.2 Selección stepwise hacia adelante
| Algoritmo: Selección stepwise hacia adelante |
|---|
| 1. Sea \(\mathcal{M_0}\) el modelo nulo (sin predictores). Este modelo solo predice la media muestral para cada observación. |
| 2. Para \(k = 0,2,\ldots,p-1\): |
a. Considera todos los \(p-k\) modelos que aumentan predictores en \(\mathcal{M_k}\) con un predictor adicional.
b. Elige el mejor de estos \(p-k\) modelos, y nómbralo \(\mathcal{M_{k+1}}\). El mejor modelo se define como aquel que tiene el mejor \(RRS\), o el más alto \(R^2\).
|
| 3. Selecciona el mejor modelo de los \(\mathcal{M_0},\ldots,\mathcal{M_p}\) usando el error de predicción en un conjunto de validación, \(C_p\), AIC, BIC o \(R^2\) ajustado. O usa el método de validación cruzada. |
6.1.1.3 Selección stepwise hacia atrás
| Algoritmo: Selección stepwise hacia atrás |
|---|
| 1. Sea \(\mathcal{M_p}\) el modelo completo, que contiene todos los \(p\) predictores. |
| 2. Para \(k = p,p-1,\ldots,1\): |
a. Considera todos los \(k\) modelos que contienen todos menos uno de los predictores en en \(\mathcal{M_k}\), para un total de \(k-1\) predictores.
b. Elige el mejor de estos \(k\) modelos, y nómbralo \(\mathcal{M_{k-1}}\). El mejor modelo se define como aquel que tiene el mejor \(RRS\), o el más alto \(R^2\).
|
| 3. Selecciona el mejor modelo de los \(\mathcal{M_0},\ldots,\mathcal{M_p}\) usando el error de predicción en un conjunto de validación, \(C_p\), AIC, BIC o \(R^2\) ajustado. O usa el método de validación cruzada. |
6.2 Regularización
La regularización es un método que nos permite restringir el proceso de estimación, se usa para evitar un posible sobre ajuste del modelo (overfitting).
Una forma de hacer regularización es donde los coeficientes de variables en el modelo no sean muy grandes (regresión ridge). Otra forma es contraer los coeficientes, llegando a tener coeficientes iguales a cero (regresión lasso).
Como regla general, el segundo enfoque suele ser mejor que el primero.
Los coeficientes regularizados se obtiene usando una función de penalidad \(p(\boldsymbol{\alpha})\) para restringir el tamaño del vector de coeficientes \(\boldsymbol{\alpha} = (\alpha_1,\cdots,\alpha_M)^T\) del predictor \(f(\mathbf{x}) = \sum_{j = 1}^{M} \alpha_jC_j(\mathbf{x})\). Los coeficientes penalizados son obtenidos como solución al problema de minimización:
\[ \hat{\boldsymbol{\alpha}}_{\lambda}= \underset{\boldsymbol{\alpha}}{\mathrm{argmin}} = \left\{\sum_{i = 1}^{n}L(y_i,f(\mathbf{x}_i))+\lambda p(\boldsymbol{\alpha}) \right\}, \] donde \(L\) es una función de pérdida y \(\lambda>0\) es un parámetro de regularización también conocido como ratio de aprendizaje.
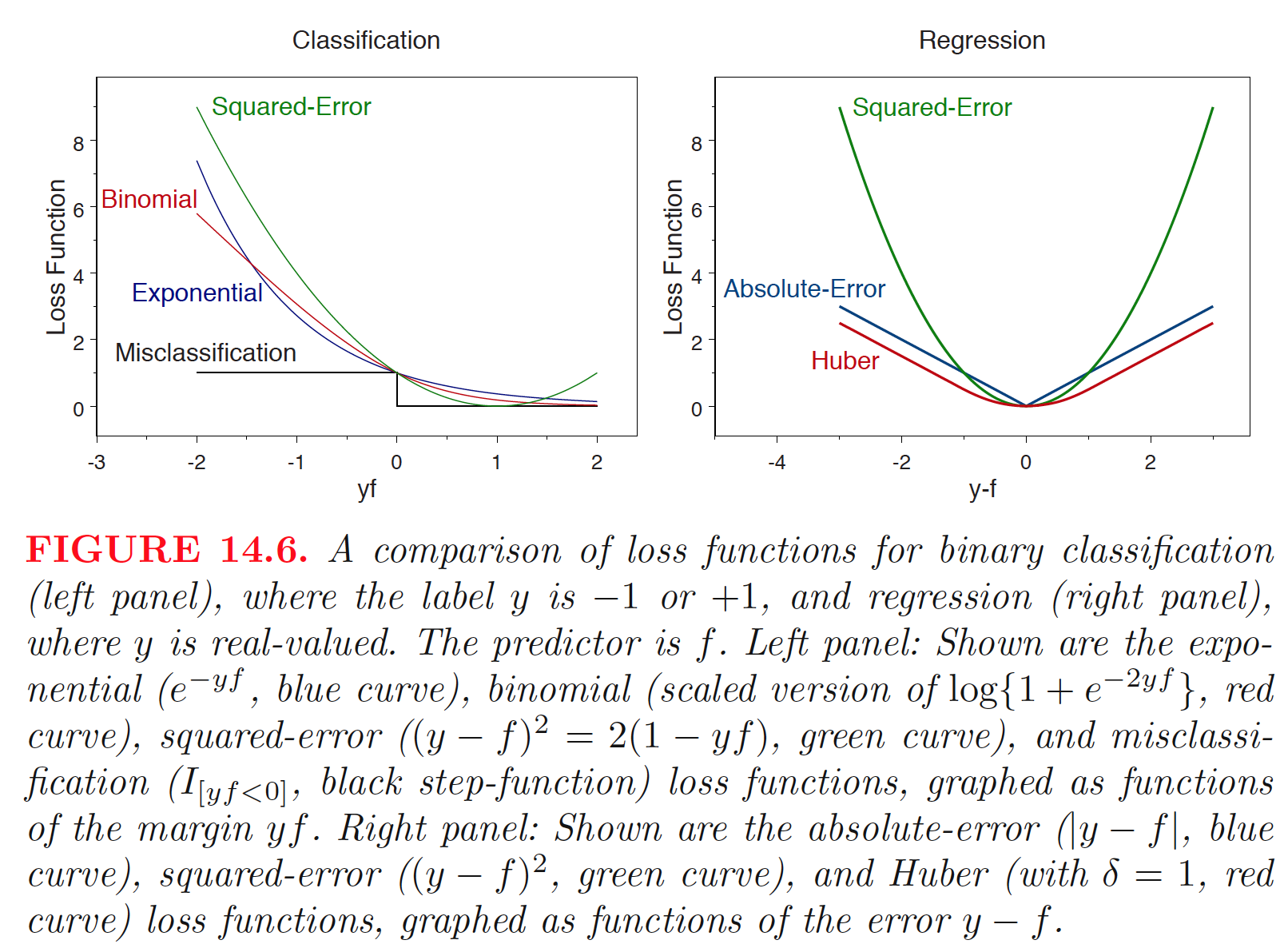
Existen diferentes opciones para funciones de pérdida:
- Exponencial:
\[ L(y,f(\mathbf{x})) = e^{-yf(\mathbf{x})}, y \in \{-1,+1\}. \]
- Logística:
\[ L(y,f_t(\mathbf{x})) = \text{log}\{1+ e^{-2yf_t(\mathbf{x})}\},y \in \{-1,+1\}. \]
- Error cuadrático:
\[ L(y,f_t(\mathbf{x})) = \frac{1}{2}(y-f_t(\mathbf{x}))^2, y \in \mathcal{R}. \]
- Error absoluto:
\[ L(y,f_t(\mathbf{x})) = |y-f_t(\mathbf{x})|, y \in \mathcal{R}. \]
- Huber
Hay dos tipos de funciones de penalidad:
- \(L_2\): esta función de penalidad restringe la suma de cuadrados de los coeficientes,
\[ p_2(\boldsymbol{\alpha})=\sum_{j = 1}^{M} \alpha_j^2. \] Cuando \(L\) combinado es una combinación convexa y usamos la pérdida de error cuadrático, el predictor de regresión penalizado óptimo es el estimador de regresión ridge.
- \(L_1\): Los coeficientes se restringen tal que su suma de valores absolutos,
\[ p_1(\boldsymbol{\alpha})=\sum_{j = 1}^{M} |\alpha_j|. \] sea menor que un valor dado. La evidencia empírica sugiere que la penalización \(L_1\) (lasso) funciona mejor cuando hay un número pequeño o mediano de coeficientes verdaderos de tamaño moderado.
6.2.1 Regresión Ridge
En mínimos cuadrados ordinarios, las estimaciones de \(\beta_0,\beta_1,\ldots,\beta_p\) se obtienen minimizando
\[ \text{RSS} = \sum_{i = 1}^n\left(y_i-\beta_0-\sum_{j=1}^p \beta_jx_{ij}\right)^2. \]
La regresión ridge es muy similar al enfoque de mínimos cuadrados, pero los coeficientes de la regresión ridge \(\hat{\beta}^R\) son los valores que minimizan
\[ \sum_{i = 1}^n\left(y_i-\beta_0-\sum_{j=1}^p \beta_jx_{ij}\right)^2+\lambda\sum_{j = 1}^{p} \beta_j^2 = \text{RSS}+\lambda\sum_{j = 1}^{p} \beta_j^2, \]
donde \(\lambda\) es un parámetro ajustable que se determina de manera separada. La influencia de la regularización se controla con \(\lambda\). Valores altos de \(\lambda\) significa más regularización y modelos más simples. Sin embargo, la regresión ridge siempre generará un modelo que incluya todos los predictores. Incrementar el valor de \(\lambda\) tenderá a reducir las magnitudes de los coeficientes, pero no resultará en la exclusión de ninguna de las variables. Notemos que la penalidad no se aplica a \(\beta_0\).
6.2.2 Regresión Lasso
\[ \sum_{i = 1}^n\left(y_i-\beta_0-\sum_{j=1}^p \beta_jx_{ij}\right)^2+\lambda\sum_{j = 1}^{p} |\beta_j| = \text{RSS}+\lambda\sum_{j = 1}^{p} |\beta_j|, \]
La penalización \(L_1\) tiene el efecto de forzar algunas de las estimaciones de coeficientes a ser exactamente iguales a cero cuando el parámetro \(\lambda\) de ajuste es suficientemente grande. Por lo tanto, lasso realiza selección de variables. Como resultado, los modelos generados a partir de lasso son generalmente mucho más fáciles de interpretar que los producidos por regresión ridge. Decimos que lasso produce modelos dispersos (sparse), es decir, modelos que involucran solo un subconjunto de variables predictoras.
6.2.2.1 Ejemplo: datos de crimen
El conjunto de datos es obtenido de (https://archive.ics.uci.edu/ml/datasets/Communities+and+Crime+Unnormalized) y se trata de comunidades en EE.UU. Son datos combinados de datos socioeconómicos del censo de 1990, datos de aplicación de la ley de la encuesta de 1990 sobre gestión de la aplicación de la ley y estadísticas administrativas y datos sobre delitos de la UCR del FBI de 1995.
A continuación se importan y limpian los datos:
# Limpieza de datos
uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/CommViolPredUnnormalizedData.txt"
crime = rio::import(uu, na.strings='?')
names(crime) <- c('communityname', 'state', 'countyCode', 'communityCode', 'fold', 'population', 'householdsize', 'racepctblack', 'racePctWhite', 'racePctAsian', 'racePctHisp', 'agePct12t21', 'agePct12t29', 'agePct16t24', 'agePct65up', 'numbUrban', 'pctUrban', 'medIncome', 'pctWWage', 'pctWFarmSelf', 'pctWInvInc', 'pctWSocSec', 'pctWPubAsst', 'pctWRetire', 'medFamInc', 'perCapInc', 'whitePerCap', 'blackPerCap', 'indianPerCap', 'AsianPerCap', 'OtherPerCap', 'HispPerCap', 'NumUnderPov', 'PctPopUnderPov', 'PctLess9thGrade', 'PctNotHSGrad', 'PctBSorMore', 'PctUnemployed', 'PctEmploy', 'PctEmplManu', 'PctEmplProfServ', 'PctOccupManu', 'PctOccupMgmtProf', 'MalePctDivorce', 'MalePctNevMarr', 'FemalePctDiv', 'TotalPctDiv', 'PersPerFam', 'PctFam2Par', 'PctKids2Par', 'PctYoungKids2Par', 'PctTeen2Par', 'PctWorkMomYoungKids', 'PctWorkMom', 'NumKidsBornNeverMar', 'PctKidsBornNeverMar', 'NumImmig', 'PctImmigRecent', 'PctImmigRec5', 'PctImmigRec8', 'PctImmigRec10', 'PctRecentImmig', 'PctRecImmig5', 'PctRecImmig8', 'PctRecImmig10', 'PctSpeakEnglOnly', 'PctNotSpeakEnglWell', 'PctLargHouseFam', 'PctLargHouseOccup', 'PersPerOccupHous', 'PersPerOwnOccHous', 'PersPerRentOccHous', 'PctPersOwnOccup', 'PctPersDenseHous', 'PctHousLess3BR', 'MedNumBR', 'HousVacant', 'PctHousOccup', 'PctHousOwnOcc', 'PctVacantBoarded', 'PctVacMore6Mos', 'MedYrHousBuilt', 'PctHousNoPhone', 'PctWOFullPlumb', 'OwnOccLowQuart', 'OwnOccMedVal', 'OwnOccHiQuart', 'OwnOccQrange', 'RentLowQ', 'RentMedian', 'RentHighQ', 'RentQrange', 'MedRent', 'MedRentPctHousInc', 'MedOwnCostPctInc', 'MedOwnCostPctIncNoMtg', 'NumInShelters', 'NumStreet', 'PctForeignBorn', 'PctBornSameState', 'PctSameHouse85', 'PctSameCity85', 'PctSameState85', 'LemasSwornFT', 'LemasSwFTPerPop', 'LemasSwFTFieldOps', 'LemasSwFTFieldPerPop', 'LemasTotalReq', 'LemasTotReqPerPop', 'PolicReqPerOffic', 'PolicPerPop', 'RacialMatchCommPol', 'PctPolicWhite', 'PctPolicBlack', 'PctPolicHisp', 'PctPolicAsian', 'PctPolicMinor', 'OfficAssgnDrugUnits', 'NumKindsDrugsSeiz', 'PolicAveOTWorked', 'LandArea', 'PopDens', 'PctUsePubTrans', 'PolicCars', 'PolicOperBudg', 'LemasPctPolicOnPatr', 'LemasGangUnitDeploy', 'LemasPctOfficDrugUn', 'PolicBudgPerPop', 'murders', 'murdPerPop', 'rapes', 'rapesPerPop', 'robberies', 'robbbPerPop', 'assaults', 'assaultPerPop', 'burglaries', 'burglPerPop', 'larcenies', 'larcPerPop', 'autoTheft', 'autoTheftPerPop', 'arsons', 'arsonsPerPop', 'ViolentCrimesPerPop', 'nonViolPerPop')
# quitamos variables con pocos datos o poca relevancia
columns_to_keep <- c(5, 6, 11:26,32:103,145)+1
crime = na.omit(crime[,columns_to_keep])Ahora escalamos los datos y los separamos en entrenamiento y prueba:
Escalamos los datos con el comando preProcess de la librería caret:
Separamos los datos en entrenamiento y prueba, 75% y 25% respectivamente con el comando createDataPartition (el parámetro list indica si se desea una lista como resultado):
set.seed(8519)
index <- createDataPartition(y, p=0.75, list=FALSE)
X_train <- X[ index, ]
X_test <- X[-index, ]
y_train <- y[index]
y_test <- y[-index]La librearía glmnet contiene la función del mismo nombre con la que se ajustan modelos GLM con regularización. El parámetro alpha indica el tipo de regularización. Si alpha = 1 es regularización lasso, si alpha = 0 es ridge.
lasso <- caret::train(y= y_train,
x = X_train,
method = 'glmnet',
tuneGrid = expand.grid(alpha = 1, lambda = 1)
)
ridge <- caret::train(y = y_train,
x = X_train,
method = 'glmnet',
tuneGrid = expand.grid(alpha = 0, lambda = 1)
) Realizamos las predicciones usando los modelos estimados:
predictions_lasso <- lasso %>% predict(X_test)
predictions_ridge <- ridge %>% predict(X_test)
# Se imprimen los R2:
data.frame(
Ridge_R2 = R2(predictions_ridge, y_test),
Lasso_R2 = R2(predictions_lasso, y_test)
)## Ridge_R2 Lasso_R2
## 1 0.6797983 0.5988638Revisamos los errores:
# Se imprime los RMSE
data.frame(
Ridge_RMSE = RMSE(predictions_ridge, y_test) ,
Lasso_RMSE = RMSE(predictions_lasso, y_test)
)## Ridge_RMSE Lasso_RMSE
## 1 376.9781 432.2993Veamos los coeficientes obtenidos:
data.frame(
as.data.frame.matrix(coef(lasso$finalModel, lasso$bestTune$lambda)),
as.data.frame.matrix(coef(ridge$finalModel, ridge$bestTune$lambda))
) %>%
rename(Lasso_coef = s0, Ridge_coef = s0.1)## Lasso_coef Ridge_coef
## (Intercept) 1.130420e+03 1132.6080108
## population 0.000000e+00 -20.1633173
## householdsize 5.666758e+02 63.9252079
## agePct12t21 -1.176333e+02 13.3219464
## agePct12t29 -1.313944e+02 -64.1113641
## agePct16t24 0.000000e+00 3.8574424
## agePct65up 0.000000e+00 -2.2223517
## numbUrban 0.000000e+00 -18.9127556
## pctUrban 9.330450e+00 18.0719286
## medIncome -4.036756e+02 -40.1100835
## pctWWage -3.058135e+02 -39.5405590
## pctWFarmSelf -9.881609e+01 -60.7961486
## pctWInvInc -4.248567e+01 -116.9446940
## pctWSocSec -3.671205e+02 -52.0449366
## pctWPubAsst 3.389220e+01 53.6143467
## pctWRetire 8.119208e+01 16.3133640
## medFamInc 0.000000e+00 -28.1067377
## perCapInc -1.123051e+02 -33.5958631
## whitePerCap 1.251772e+02 109.9367670
## NumUnderPov -6.926150e+02 -52.9742410
## PctPopUnderPov -7.922162e+00 -24.7666068
## PctLess9thGrade -6.074581e+01 -55.7898435
## PctNotHSGrad -1.443651e+02 -36.5525729
## PctBSorMore 2.130984e+02 53.7561098
## PctUnemployed 4.605313e+01 45.0329162
## PctEmploy 1.847667e+01 -34.3921946
## PctEmplManu -1.972805e+02 -98.7474609
## PctEmplProfServ 0.000000e+00 21.6229637
## PctOccupManu 4.413362e+02 104.6704919
## PctOccupMgmtProf 1.561198e+02 39.3165819
## MalePctDivorce 0.000000e+00 60.3490606
## MalePctNevMarr 4.990046e+00 29.3530136
## FemalePctDiv -3.961422e+01 -16.0748567
## TotalPctDiv 0.000000e+00 13.7176081
## PersPerFam -2.291248e+02 -3.2830146
## PctFam2Par 0.000000e+00 -83.9731317
## PctKids2Par -6.569872e+02 -150.1979018
## PctYoungKids2Par 6.963574e+01 -23.3918684
## PctTeen2Par 1.088942e+02 -5.9783711
## PctWorkMomYoungKids -1.005379e+02 0.9467168
## PctWorkMom 9.220252e+01 32.3961499
## NumKidsBornNeverMar 1.990928e+02 -13.7559394
## PctKidsBornNeverMar 5.287453e-04 150.8676448
## NumImmig 2.252002e+02 61.0197149
## PctImmigRecent 4.719160e+01 -16.7025432
## PctImmigRec5 -1.030924e+02 -60.9153121
## PctImmigRec8 -1.485752e+02 -8.1538351
## PctImmigRec10 2.976061e+02 104.4518321
## PctRecentImmig -1.202809e+02 -37.2421608
## PctRecImmig5 0.000000e+00 -3.0547671
## PctRecImmig8 0.000000e+00 2.1847088
## PctRecImmig10 -2.604227e+02 30.9523183
## PctSpeakEnglOnly 0.000000e+00 46.8223834
## PctNotSpeakEnglWell 2.643543e+00 25.5978791
## PctLargHouseFam 5.067664e+02 -7.7171054
## PctLargHouseOccup -8.214177e+02 -60.9426156
## PersPerOccupHous 0.000000e+00 -0.2984062
## PersPerOwnOccHous 1.854213e+02 63.0225693
## PersPerRentOccHous -2.851028e+02 -45.3390185
## PctPersOwnOccup 0.000000e+00 24.9957897
## PctPersDenseHous 4.046975e+02 77.2752138
## PctHousLess3BR 3.997264e+01 49.3260040
## MedNumBR -4.049265e+01 -13.3199287
## HousVacant 3.060022e+02 75.2517723
## PctHousOccup 1.590144e+01 -7.5891021
## PctHousOwnOcc 4.838100e+01 14.5887569
## PctVacantBoarded 3.827256e+01 55.2052686
## PctVacMore6Mos 2.473944e+01 19.6278759
## MedYrHousBuilt 1.522281e+02 93.1131168
## PctHousNoPhone 2.271944e+01 26.8616927
## PctWOFullPlumb -1.001378e+02 -30.6673892
## OwnOccLowQuart 0.000000e+00 -31.6475492
## OwnOccMedVal 0.000000e+00 -7.0279234
## OwnOccHiQuart -1.142313e+02 -31.6718068
## OwnOccQrange -2.594090e+01 -23.6864496
## RentLowQ -4.709927e+02 -58.4116395
## RentMedian 2.964951e+01 36.0966448
## RentHighQ -7.345267e+01 -14.2412512
## RentQrange -3.348517e-01 67.1453388
## MedRent 8.418653e+02 75.6144996
## MedRentPctHousInc -4.415355e+01 -12.4628225
## MedOwnCostPctInc -3.418865e+01 35.6726206
## MedOwnCostPctIncNoMtg -5.692937e+01 -80.2774801
## NumInShelters -2.558319e+01 25.6507248
## NumStreet 7.019079e+01 25.6110485
## PctForeignBorn 3.040272e+02 72.1198686
## PctBornSameState -1.064257e+01 -23.3078839
## PctSameHouse85 5.027221e+01 44.9946815
## PctSameCity85 1.737350e+01 2.5094687
## PctSameState85 4.649409e+01 17.7969544
## LemasSwornFT -1.195124e+01 -31.4780697Ahora, elegimos el parámetro de regularización con la ayuda de tuneGrid. Los modelos con la puntuación \(R^2\) cuadrado más alta nos darán los mejores parámetros.
parameters <- c(seq(0.1, 2, by =0.1) , seq(2, 5, 0.5) , seq(5, 500, 5))
lasso <- caret::train(y = y_train,
x = X_train,
method = 'glmnet',
tuneGrid = expand.grid(alpha = 1, lambda = parameters) ,
metric = "Rsquared"
)
ridge <- caret::train(y = y_train,
x = X_train,
method = 'glmnet',
tuneGrid = expand.grid(alpha = 0, lambda = parameters),
metric = "Rsquared"
)
linear <- caret::train(y = y_train,
x = X_train,
method = 'lm',
metric = "Rsquared"
)
print(paste0('Lasso (mejores parámetros): ' , lasso$finalModel$lambdaOpt))## [1] "Lasso (mejores parámetros): 230"## [1] "Ridge (mejores parámetros): 500"Revisamos el \(R^2\) y el \(\text{RMSE}\):
predictions_lasso <- lasso %>% predict(X_test)
predictions_ridge <- ridge %>% predict(X_test)
predictions_lin <- linear %>% predict(X_test)
data.frame(
Ridge_R2 = R2(predictions_ridge, y_test),
Lasso_R2 = R2(predictions_lasso, y_test),
Linear_R2 = R2(predictions_lin, y_test)
)## Ridge_R2 Lasso_R2 Linear_R2
## 1 0.6737963 0.6189773 0.4857502data.frame(
Ridge_RMSE = RMSE(predictions_ridge, y_test) ,
Lasso_RMSE = RMSE(predictions_lasso, y_test) ,
Linear_RMSE = RMSE(predictions_lin, y_test)
)## Ridge_RMSE Lasso_RMSE Linear_RMSE
## 1 375.0716 431.1954 508.1641Veamos los coeficientes estimados:
## [1] "Los mejores coeficientes estimados"data.frame(
lasso = as.data.frame.matrix(coef(lasso$finalModel, lasso$finalModel$lambdaOpt)),
ridge = as.data.frame.matrix(coef(ridge$finalModel, ridge$finalModel$lambdaOpt)),
linear = (linear$finalModel$coefficients)
) %>% rename(lasso = s0, ridge = s0.1)## lasso ridge linear
## (Intercept) 1147.6506 1134.9431646 1122.658115
## population 0.0000 0.3606813 -10871.577689
## householdsize 0.0000 14.8157146 840.365581
## agePct12t21 0.0000 3.3151221 -194.637075
## agePct12t29 0.0000 -27.4810827 -177.592993
## agePct16t24 0.0000 -11.2192172 -60.593345
## agePct65up 0.0000 -2.5271129 -25.036687
## numbUrban 0.0000 0.5120029 11053.501418
## pctUrban 0.0000 22.0555885 -33.934401
## medIncome 0.0000 -7.9746127 -1248.079959
## pctWWage 0.0000 -8.4534822 -474.962612
## pctWFarmSelf 0.0000 -40.9593232 -132.054694
## pctWInvInc 0.0000 -51.7442717 -2.825268
## pctWSocSec 0.0000 -13.1436408 -612.355509
## pctWPubAsst 0.0000 29.1270431 150.967869
## pctWRetire 0.0000 -7.2210071 61.432506
## medFamInc 0.0000 -8.2261429 652.356848
## perCapInc 0.0000 -1.3994315 -148.710400
## whitePerCap 0.0000 42.6074709 104.460205
## NumUnderPov 0.0000 -3.5031683 -1345.830586
## PctPopUnderPov 0.0000 11.0609017 -116.646514
## PctLess9thGrade 0.0000 -21.3138453 -214.436395
## PctNotHSGrad 0.0000 -0.3011144 -144.805596
## PctBSorMore 0.0000 5.7726396 151.457508
## PctUnemployed 0.0000 28.2245967 -10.779315
## PctEmploy 0.0000 -22.1852667 68.897050
## PctEmplManu 0.0000 -55.7591311 -159.479930
## PctEmplProfServ 0.0000 15.6349282 -49.320027
## PctOccupManu 0.0000 5.7162408 489.784243
## PctOccupMgmtProf 0.0000 5.6746190 405.405934
## MalePctDivorce 0.0000 41.3376924 162.111945
## MalePctNevMarr 0.0000 21.0935986 61.978109
## FemalePctDiv 0.0000 29.5533304 313.512501
## TotalPctDiv 0.0000 35.7865206 -539.740385
## PersPerFam 0.0000 12.8434139 -892.724350
## PctFam2Par 0.0000 -63.3791097 155.309904
## PctKids2Par -274.6816 -77.2658142 -1076.322008
## PctYoungKids2Par 0.0000 -48.7372012 63.766829
## PctTeen2Par 0.0000 -52.3234082 228.107231
## PctWorkMomYoungKids 0.0000 15.4966945 -139.933827
## PctWorkMom 0.0000 15.5887797 148.001458
## NumKidsBornNeverMar 0.0000 7.3792925 823.136293
## PctKidsBornNeverMar 111.9105 90.1571272 -275.716625
## NumImmig 0.0000 8.8744033 246.463966
## PctImmigRecent 0.0000 -14.4238048 386.938247
## PctImmigRec5 0.0000 -9.2828834 -488.396949
## PctImmigRec8 0.0000 7.8179446 -283.578005
## PctImmigRec10 0.0000 32.7165884 553.681794
## PctRecentImmig 0.0000 -5.4882242 -1499.140927
## PctRecImmig5 0.0000 3.5802580 2495.947793
## PctRecImmig8 0.0000 7.7343690 218.683864
## PctRecImmig10 0.0000 15.4764031 -2393.680669
## PctSpeakEnglOnly 0.0000 20.7302810 -120.364986
## PctNotSpeakEnglWell 0.0000 -3.5952710 28.471431
## PctLargHouseFam 0.0000 15.1526969 1734.747671
## PctLargHouseOccup 0.0000 2.2432740 -2074.484590
## PersPerOccupHous 0.0000 5.8992397 213.898997
## PersPerOwnOccHous 0.0000 21.7596068 595.806448
## PersPerRentOccHous 0.0000 -2.9449743 -661.765417
## PctPersOwnOccup 0.0000 1.5507281 -1620.311758
## PctPersDenseHous 0.0000 30.0871764 867.027964
## PctHousLess3BR 0.0000 21.8513253 66.384520
## MedNumBR 0.0000 -2.4237333 -47.465555
## HousVacant 0.0000 23.5587002 460.698398
## PctHousOccup 0.0000 -22.2653743 35.298779
## PctHousOwnOcc 0.0000 -0.1461844 1686.420107
## PctVacantBoarded 0.0000 53.7638070 40.344261
## PctVacMore6Mos 0.0000 13.4318226 62.599055
## MedYrHousBuilt 0.0000 34.6951265 158.543121
## PctHousNoPhone 0.0000 19.3481570 53.051654
## PctWOFullPlumb 0.0000 0.8501767 -148.569984
## OwnOccLowQuart 0.0000 -10.5489552 -360.390700
## OwnOccMedVal 0.0000 -6.2428537 417.935802
## OwnOccHiQuart 0.0000 -4.8448381 -391.086418
## OwnOccQrange 0.0000 4.7102975 NA
## RentLowQ 0.0000 -14.9873332 -718.093140
## RentMedian 0.0000 2.9430115 260.558601
## RentHighQ 0.0000 -0.9732736 -339.982879
## RentQrange 0.0000 23.5623906 NA
## MedRent 0.0000 10.6792040 1195.115997
## MedRentPctHousInc 0.0000 12.5207380 -39.531086
## MedOwnCostPctInc 0.0000 22.1233026 -94.471559
## MedOwnCostPctIncNoMtg 0.0000 -31.7979290 6.990649
## NumInShelters 0.0000 13.5471871 -39.885696
## NumStreet 0.0000 5.7852204 26.024385
## PctForeignBorn 0.0000 17.5176905 935.263522
## PctBornSameState 0.0000 -24.2491275 124.249332
## PctSameHouse85 0.0000 19.7928596 144.115665
## PctSameCity85 0.0000 3.2963396 -30.985328
## PctSameState85 0.0000 6.1610943 -37.785119
## LemasSwornFT 0.0000 0.6214069 -271.999351Nuestro puntaje subió un poco (lasso). Construyamos gráficos de coeficientes para ver cómo el valor de lambda influye en los coeficientes de ambos modelos.
Usaremos la función glmnet para entrenar los modelos y luego usaremos la función plot() que produce un diagrama de perfil de coeficientes de las rutas de los coeficientes para un objeto glmnet ajustado.
El parámetro xvar de plot() define lo que está en el eje X, y hay 3 valores posibles que puede tomar: norm, lambda o dev, donde norm es la norma \(L_1\) de los coeficientes. , lambda para la secuencia log-lambda y dev es el porcentaje de desviación explicado. Lo configuraremos en lambda.
Para entrenar glment, necesitamos convertir nuestro objeto X_train en una matriz.
# Fijamos los valores de los coeficientes
paramLasso <- seq(0, 500, 5)
paramRidge <- seq(0, 500, 5)
# Convertimos en matriz para glmnet
X_train_m <- as.matrix(X_train)
# Construimos los modelos para los valores de lambda values of lambda
rridge <- glmnet(
x = X_train_m,
y = y_train,
alpha = 0, #Ridge
lambda = paramRidge
)
llaso <- glmnet(
x = X_train_m,
y = y_train,
alpha = 1, #Lasso
lambda = paramLasso
)
plot(rridge,xvar = c("lambda"),label = TRUE)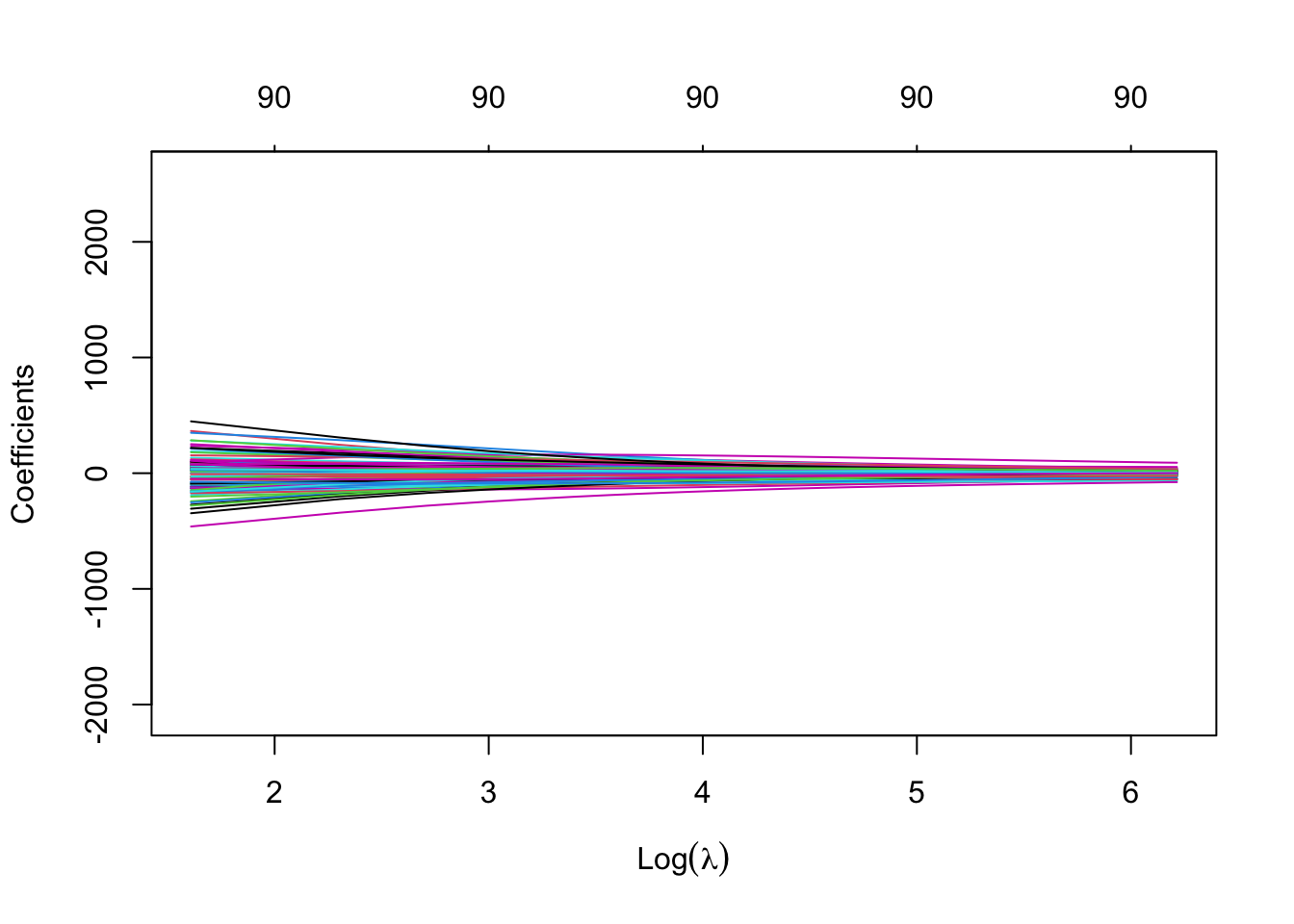
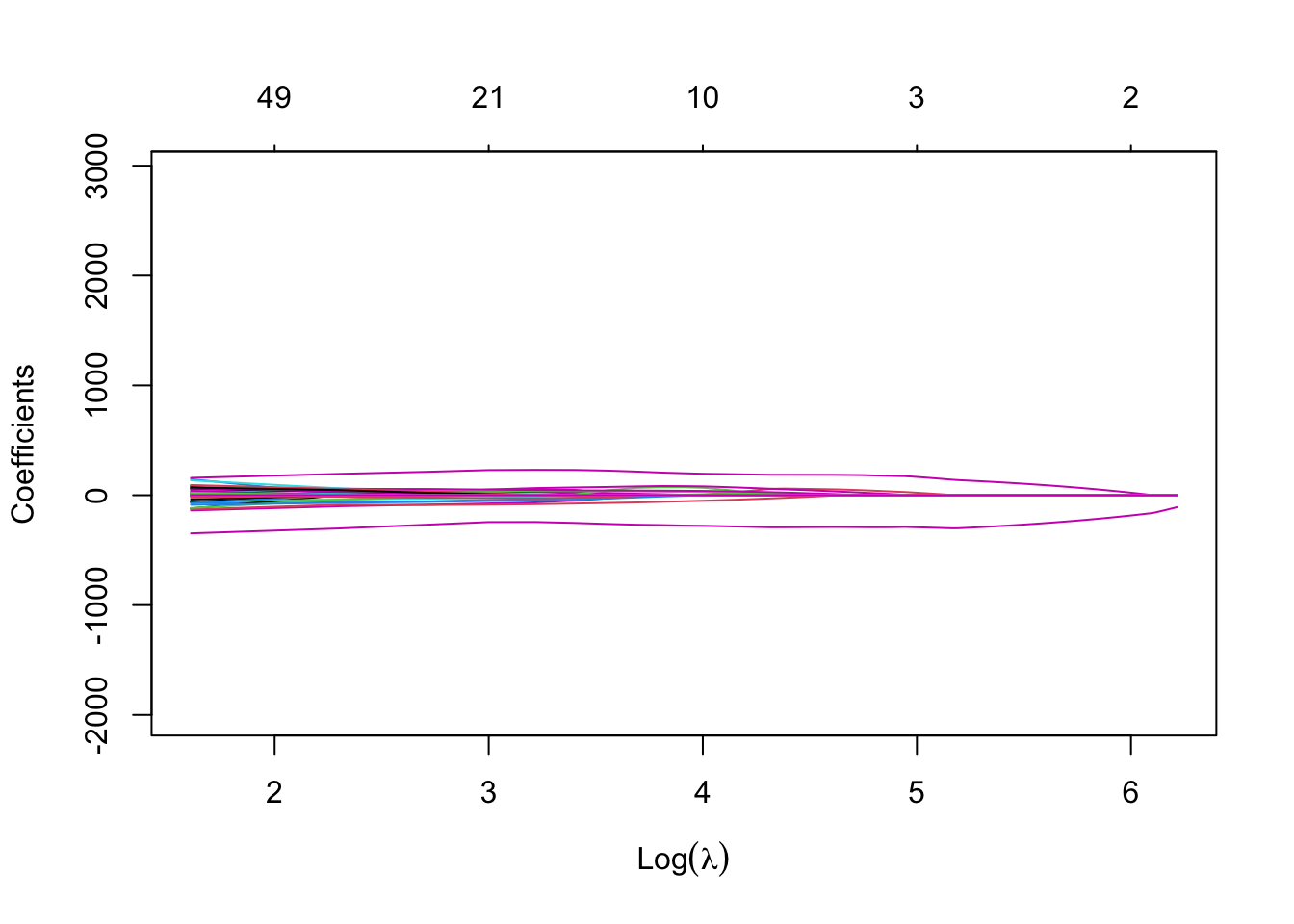
Usamos CV para visualizar la ganancia en MSE:
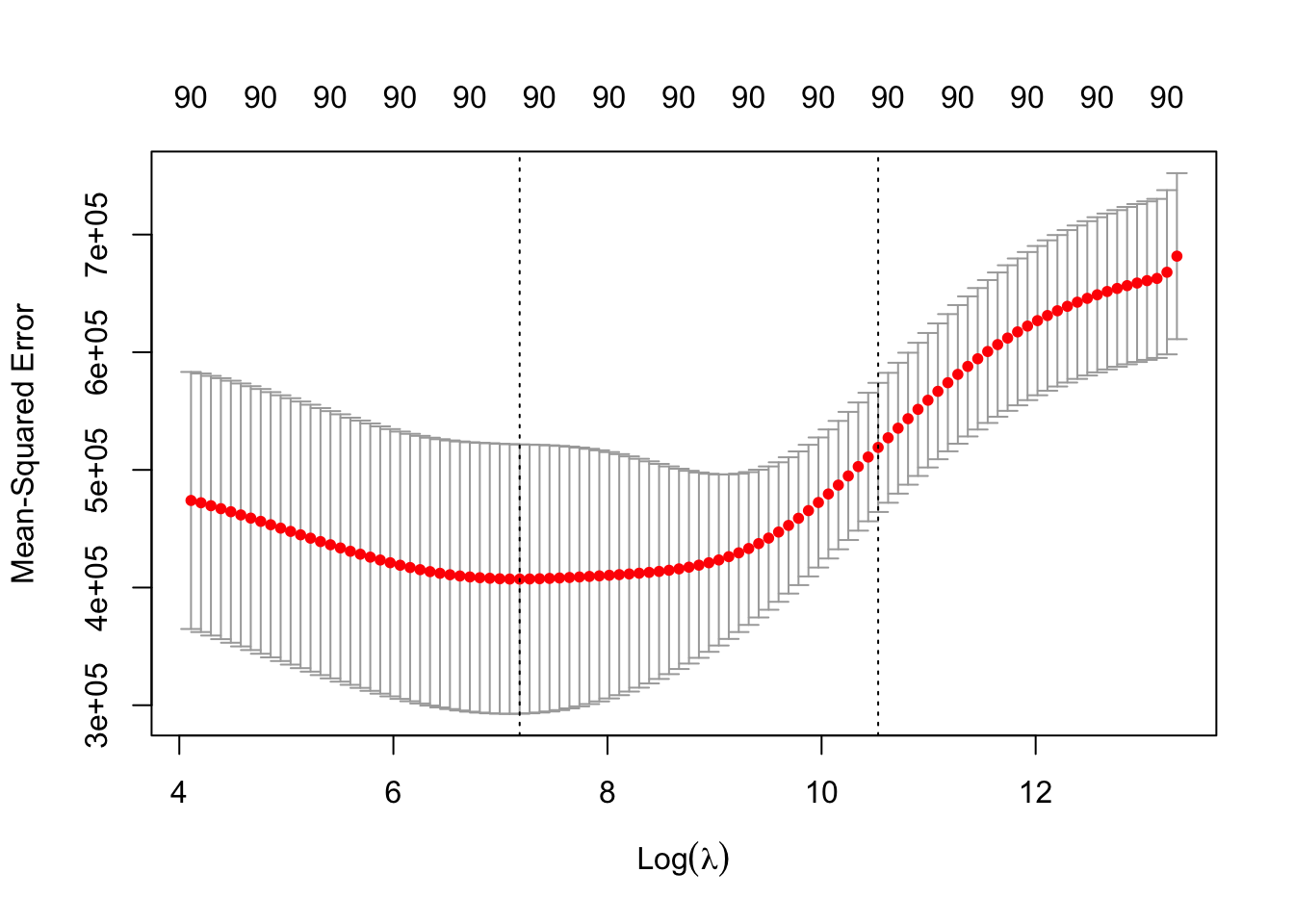
## [1] 1312.253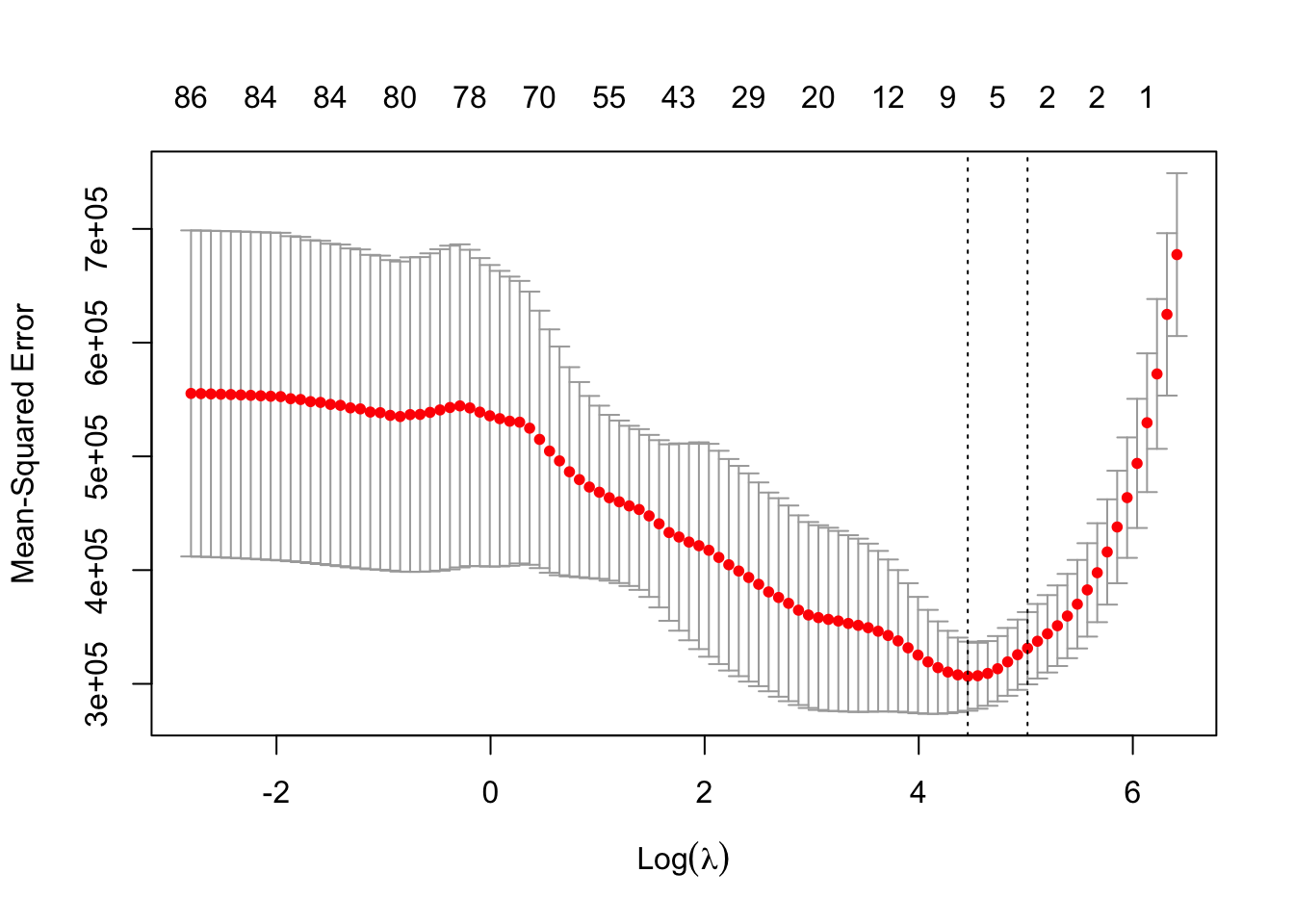
## [1] 86.33751Revisamos el \(R^2\) y el \(\text{RMSE}\):
# Convertimos en matriz para glmnet
X_test_m <- as.matrix(X_test)
predictions_cv_ridge <- cv.out_ridge %>% predict(X_test_m,s =bestlam_ridge)
predictions_cv_lasso <- cv.out_lasso %>% predict(X_test_m,s =bestlam_lasso)
data.frame(
Ridge_R2 = R2(predictions_ridge, y_test),
Lasso_R2 = R2(predictions_lasso, y_test),
Linear_R2 = R2(predictions_lin, y_test),
CV_ridge_R2 = R2(predictions_cv_ridge, y_test),
CV_lasso_R2 = R2(predictions_cv_lasso, y_test)
)## Ridge_R2 Lasso_R2 Linear_R2 s0 s0.1
## 1 0.6737963 0.6189773 0.4857502 0.671287 0.6630695data.frame(
Ridge_RMSE = RMSE(predictions_ridge, y_test) ,
Lasso_RMSE = RMSE(predictions_lasso, y_test) ,
Linear_RMSE = RMSE(predictions_lin, y_test),
RMSE_ridge_R2 = RMSE(predictions_cv_ridge, y_test),
RMSE_lasso_R2 = RMSE(predictions_cv_lasso, y_test)
)## Ridge_RMSE Lasso_RMSE Linear_RMSE RMSE_ridge_R2 RMSE_lasso_R2
## 1 375.0716 431.1954 508.1641 372.903 384.7345