8  Linear Transformations

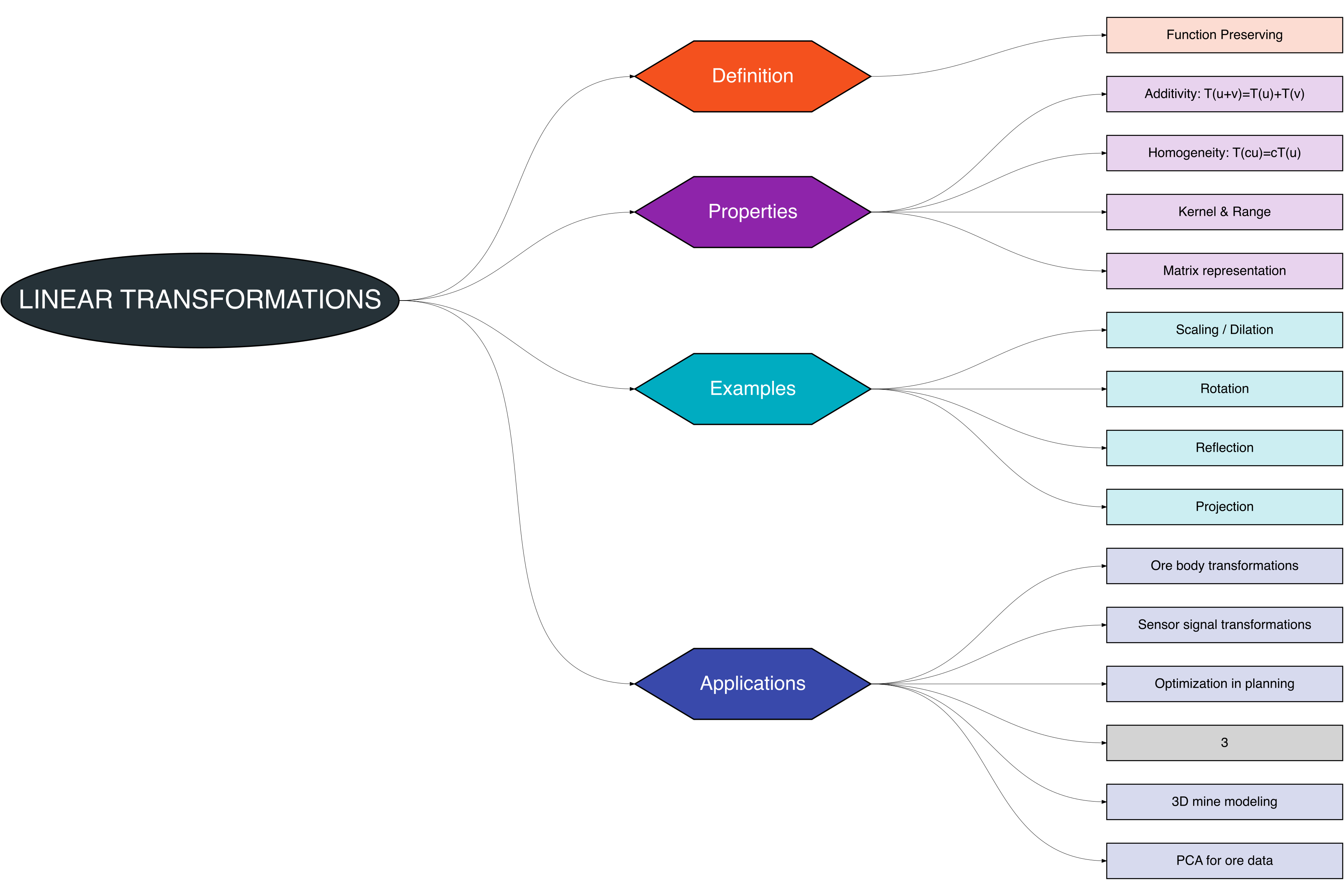
In this chapter, we explore the concept of linear transformations in vector and inner product spaces, along with their fundamental properties. A mind map provides a structured overview of the key topics discussed:

Figure 8.1: Mind Map of Linear Transformations

Linear transformations are functions between vector spaces that preserve vector addition and scalar multiplication. They provide a framework to map vectors from one space to another while maintaining the structure of the space.

In the context of mining engineering:

• Ore Body Mapping & Alignment: Linear transformations can represent rotations, scaling, and translations of ore bodies to align geological survey data from multiple sources, ensuring consistency in 3D models chiles2012?.
  
• Geotechnical Sensor Data Processing: Measurements from strain gauges, accelerometers, or seismic sensors can be linearly transformed to extract independent components, filter noise, and improve signal interpretation [1].
  
• Production & Resource Planning: Extraction schedules, equipment deployment, and workforce assignments can be modeled as linear transformations to optimize operations under given constraints meyer2000?.
  
• 3D Mine Design & Modeling: Tunnel layouts, boreholes, and ore body geometries can be transformed in \(\mathbb{R}^3\) to enable visualization, simulation, and coordinate system adjustments for mine planning rubinstein2016?.
  
• Dimensionality Reduction of Ore Grade Data: Linear transformations such as Principal Component Analysis (PCA) identify orthogonal directions that maximize variance, helping to simplify datasets, reduce computational complexity, and enhance geostatistical modeling [1].

8.1 Definition

A transformation \(T: V \to W\) between vector spaces \(V\) and \(W\) is linear if, for all \(u, v \in V\) and scalars \(c \in \mathbb{R}\):

\[ T(u + v) = T(u) + T(v), \quad T(cu) = c \, T(u) \]

Key concepts:

• Kernel (Null Space):
  \[ \text{ker}(T) = \{ v \in V : T(v) = 0 \} \]

• Range (Image):
  \[ \text{range}(T) = \{ T(v) : v \in V \} \]

• Matrix Representation:
  Every linear transformation can be represented by a matrix relative to chosen bases, enabling computation and composition.

8.2 Properties

• Additivity:
  \[ T(u+v) = T(u) + T(v) \]

• Homogeneity (Scalar Multiplication):
  \[ T(c u) = c \, T(u) \]

• Kernel & Range: Describe the null space and image of \(T\).

• Matrix Representation: Enables computation, composition, and application of transformations.

8.3 Examples

1. Scaling / Dilation:
   \[ T(x) = k x \]
   Stretches or shrinks vectors by a factor \(k\).

2. Rotation:
   Rotates vectors around an origin in \(\mathbb{R}^2\) or \(\mathbb{R}^3\).

3. Reflection:
   Reflects vectors across a line, plane, or hyperplane.

4. Projection:
   Projects vectors onto a subspace.

8.4 Applications

• Ore Body Transformations:
  Linear transformations can adjust survey data for modeling and alignment of ore bodies chiles2012?.

• Sensor Signal Analysis:
  Transform signals from monitoring equipment for feature extraction or filtering, enabling better interpretation of geotechnical or seismic data [1].

• Optimization of Resources:
  Apply linear mappings to planning constraints and allocation strategies for workforce, equipment, and materials meyer2000?.

• 3D Mine Modeling:
  Transform mine coordinates for visualization, simulation, and planning in \(\mathbb{R}^3\) rubinstein2016?.

• PCA Transformations:
  Reduce dimensionality of ore grade datasets while preserving key variance, aiding geostatistical modeling and predictive analytics [1].

References

[1]

Golub, G. H. and Loan, C. F. V., Matrix computations, Johns Hopkins University Press, Baltimore, MD, 2013