10 Case Studies
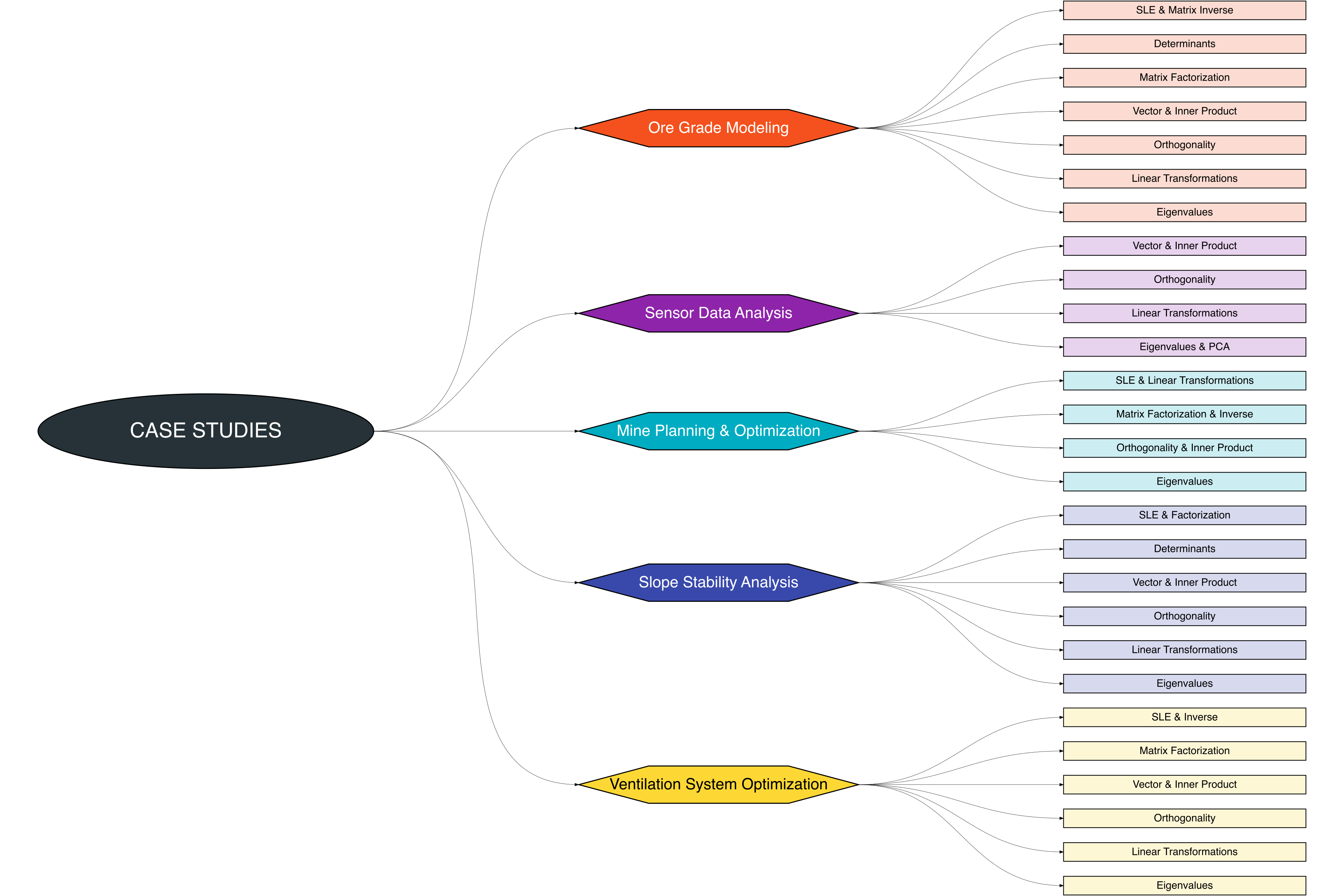
In this chapter, we present case studies applying all the concepts covered in the previous chapters, from systems of linear equations to eigenvalues, within the context of mining engineering. A mind map provides a structured overview of how the topics interrelate:

10.1 Ore Grade Modeling
- SLE & Matrix Inverse: Solve for unknown ore grade distributions from sample measurements using linear systems.
- Determinants: Check solvability and dependency of ore sampling equations.
- Matrix Factorization (LU/Cholesky): Efficiently solve large sparse systems representing ore grade correlations.
- Vector & Inner Product Spaces: Represent ore grades as vectors and measure similarity between samples.
- Orthogonality: Decompose ore grade vectors into independent components.
- Linear Transformations: Rotate or scale ore body data for alignment of surveys.
- Eigenvalues: Determine principal directions of ore grade variability for PCA and risk assessment.
10.2 Sensor Data Analysis
- Vector Spaces & Inner Products: Model sensor readings as vectors to measure correlations.
- Orthogonality: Separate independent signal components for anomaly detection.
- Linear Transformations: Filter and transform signals for feature extraction.
- Eigenvalues & PCA: Reduce dimensionality while preserving important variance in geotechnical sensor datasets.
10.3 Mine Planning and Optimization
- SLE & Linear Transformations: Model resource allocation, scheduling, and material flows.
- Matrix Factorization & Inverse: Solve optimization problems efficiently using linear algebra.
- Orthogonality & Inner Product: Project tasks onto independent directions to minimize interference.
- Eigenvalues: Analyze stiffness matrices, stress tensors, and vibration modes to ensure tunnel stability and equipment safety.
10.4 Slope Stability Analysis
- SLE & Matrix Factorization: Solve equilibrium equations for slopes under various load conditions.
- Determinants: Check dependency of stress and force equations to ensure solvability.
- Vector & Inner Product Spaces: Represent force vectors and displacement vectors in slope models.
- Orthogonality: Decompose stress and displacement vectors into independent components.
- Linear Transformations: Transform slope models under different coordinate systems for simulation.
- Eigenvalues: Determine critical directions of stress and potential failure planes.
10.5 Ventilation System Optimization
- SLE & Matrix Inverse: Solve airflow distribution and pressure balance equations in underground tunnels.
- Matrix Factorization (LU/Cholesky): Efficiently solve large systems representing complex ventilation networks.
- Vector & Inner Product Spaces: Model airflow vectors and velocity correlations.
- Orthogonality: Separate independent airflow components for identifying bottlenecks.
- Linear Transformations: Simulate airflow changes due to opening/closing of shafts or fans.
- Eigenvalues: Identify dominant modes in airflow or pressure fluctuations for system stability and optimization.
