13.4 Instrumental variables (IV)
In many real-world situations, we face biases such as those described in the previous paragraph, arising from measurement errors, omission of relevant variables, and similar issues. Even in these cases, it is still possible to identify the causal effect. One common strategy is to use a set of instrumental variables (\(\mathbf{Z}\)) that satisfy two key conditions:
Relevance, meaning the instruments are correlated with the treatment: \[ \mathbf{Z}_i \not\perp D_i. \]
Exogeneity, which in the linear model requires: \[\begin{equation*} \mathbb{E}[\mu_i \mid \mathbf{Z}_i] = 0 \end{equation*}\]
and, in terms of potential outcomes, entails:
- Exclusion restriction: instruments affect the outcome only through the treatment: \[ Y_i(D_i = d, \mathbf{Z}_i = \mathbf{z}) = Y_i(D_i = d, \mathbf{Z}_i = \mathbf{z}') = Y_i(D_i = d), \quad d \in \{0,1\}, \]
- Marginal exchangeability: instruments are independent of the potential outcomes: \[ \mathbf{Z}_i \perp \{ Y_i(1), Y_i(0) \}. \]
Relevance is testable, typically by checking whether instruments significantly predict the endogenous variable (Staiger and Stock 1997; Cragg and Donald 1993; Kleibergen and Paap 2006; Stock and Yogo 2005). However, weak instruments—those that exhibit only a weak association with the treatment—can lead to serious consequences, including a high level of uncertainty and the potential amplification of even small biases when estimating the causal effect.
Exogeneity is fundamentally untestable (Guido W. Imbens and Angrist 1994). However, when the number of instruments exceeds the number of endogenous variables, the Sargan test (or its robust version, the Hansen \(J\)-test) can be used to assess the validity of overidentifying restrictions. This test should not be misinterpreted as a direct test of the exclusion restriction. Instead, it evaluates whether the overidentifying restrictions implied by the IV model hold. Specifically, the null hypothesis states that all instruments are jointly uncorrelated with the structural error term, \(\mathbb{E}[\mathbf{Z}^\top \mu] = \mathbf{0}\) (Sargan 1958; Hansen 1982).
If the test rejects, it indicates that at least one instrument is invalid, but it does not reveal whether the violation arises from a failure of the exclusion restriction, correlation with unobserved confounders, or model misspecification. Conversely, if the test fails to reject, it only suggests that the sample moment conditions do not provide evidence against instrument validity under the maintained model. This outcome does not prove that the exclusion restrictions hold: the test may have low power, a mix of valid and invalid instruments could pass if violations “cancel out”, and if the model is misspecified, a “passing” test is uninformative.
In general, the exclusion restriction concerns unobservables (no correlation with the error term). Since the error term is not observed, the exclusion restriction can never be proven from the data; we can only look for evidence against it. Therefore, while the Sargan test is informative about overall instrument validity, it is not a separate or definitive test of the exclusion restriction (Jeffrey M. Wooldridge 2010; Hayashi 2000).
The following figure illustrates a situation where pre-treatment variables that influence both the treatment and the outcome are partially observed or measured with error. In such cases, an instrument can help identify the causal effect of the treatment on the outcome.
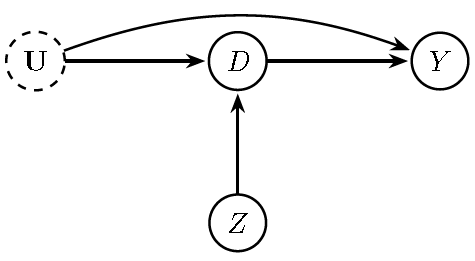
Figure 13.7: Directed Acyclic Graph (DAG) showing an instrumental variable \(Z\) used to identify the causal effect of \(D\) on \(Y\) when some confounders \(U\) (dashed) are unobserved or measured with error.
However, the two conditions for instruments (relevance and exogeneity) only imply partial identification of the Local Average Treatment Effect (LATE; see below, and Manski (1989); Manski (1990); Manski (1995); Manski (2003) for detailed treatments of partial identification). Thus, it is necessary to impose a third condition to achieve point identification of a particular treatment effect using IV. This condition is monotonicity, which asserts that the instrument moves all units’ treatment decisions in the same direction, that is,
\[
D_i(1)\geq D_i(0), \quad i=1,2,\dots,N,
\]
assuming a binary instrument \(Z_i \in \{0,1\}\).
Note that monotonicity is also fundamentally untestable (Guido W. Imbens and Angrist 1994), as it refers to unobserved potential outcomes. However, its validity can be argued in the context of each application. We can examine whether the instrument shifts treatment in the expected direction. Moreover, if rich covariates are available, we can stratify by them and verify that, within each subgroup, the instrument increases (or at least does not decrease) the probability of treatment. For instance, we can analyze the cumulative distribution functions of the outcome when the binary instrumental variable takes values of 0 and 1; if the functions do not cross, this would suggest plausibility of the monotonicity assumption (Ramı́rez-Hassan et al. 2023).
In the case where \(Z_i\) denotes the assignment to treatment and \(D_i\) the actual treatment status, there are four potential groups: always-takers (\(D = 1 \mid Z = 1\) and \(D = 1 \mid Z = 0\)), never-takers (\(D = 0 \mid Z = 1\) and \(D = 0 \mid Z = 0\)), compliers (\(D = 1 \mid Z = 1\) and \(D = 0 \mid Z = 0\)), and defiers (\(D = 0 \mid Z = 1\) and \(D = 1 \mid Z = 0\)). Note that these groups are not identified; for instance, we do not know whether an individual with \(Z_i = 1\) and \(D_i = 1\) is a complier or an always-taker. The monotonicity assumption rules out defiers, meaning that the instrument (assignment to treatment) either does not change treatment status or only increases it.
The table displays the distribution of unit types when defiers are ruled out by the monotonicity assumption.
| Instrument | \(D_i = 0\) | \(D_i = 1\) |
|---|---|---|
| \(Z_i = 0\) | Compliers, Never-takers | Always-takers |
| \(Z_i = 1\) | Never-takers | Compliers, Always-takers |
From this table we can identify the proportions of compliance types (\(C\)) as follows. The probability of always-takers (a) is
\[
P(C_i = a) = P(D_i=1 \mid Z_i=0),
\]
and the probability of never-takers (n) is
\[
P(C_i = n) = P(D_i=0 \mid Z_i=1).
\]
For compliers (c), note that
\[
P(D_i=1 \mid Z_i=1) = P(C_i=c) + P(C_i=a),
\]
so that
\[
P(C_i = c) = P(D_i=1 \mid Z_i=1) - P(D_i=1 \mid Z_i=0).
\]
Equivalently, using \(D_i=0\),
\[
P(D_i=0 \mid Z_i=0) = P(C_i=n) + P(C_i=c),
\]
so that
\[
P(C_i = c) = P(D_i=0 \mid Z_i=0) - P(D_i=0 \mid Z_i=1).
\]
Therefore, under relevance, exogeneity, monotonicity, and SUTVA, IV methods allow identification of the causal effect for the subgroup of compliers, that is, individuals who take the treatment when encouraged by the instrument and do not take it otherwise (Guido W. Imbens and Angrist 1994; Angrist, Imbens, and Rubin 1996). This estimand is known as the Local Average Treatment Effect (LATE) because it applies to a specific subpopulation rather than the entire population (Hernán and Robins 2020): \[ \tau_{LATE} = \mathbb{E}[Y_i(1)-Y_i(0)\mid D_i(1)=1, D_i(0)=0]. \]
We define \(Y_i(z_i,D_i(z))\) to be the outcome for unit \(i\) if exposed to treatment \(D_i(z)\) after being assigned to treatment \(z\). Therefore, the Intention-to-Treat (ITT) causal effect of \(Z_i\) on \(Y_i\) is \(\mathbb{E}[Y_i(1,D_i(1))-Y_i(0,D_i(0))]\), and can be expressed as:\[ \begin{aligned} \underbrace{\mathbb{E}[Y_i(1,D_i(1))-Y_i(0,D_i(0))\mid D_i(1)=1,D_i(0)=1]\times P(D_i(1)=1,D_i(0)=1)}_{\text{always-takers}} \\ +\underbrace{\mathbb{E}[Y_i(1,D_i(1))-Y_i(0,D_i(0))\mid D_i(1)=0,D_i(0)=0]\times P(D_i(1)=0,D_i(0)=0)}_{\text{never-takers}} \\ +\underbrace{\mathbb{E}[Y_i(1,D_i(1))-Y_i(0,D_i(0))\mid D_i(1)=1,D_i(0)=0]\times P(D_i(1)=1,D_i(0)=0)}_{\text{compliers}} \\ +\underbrace{\mathbb{E}[Y_i(1,D_i(1))-Y_i(0,D_i(0))\mid D_i(1)=0,D_i(0)=1]\times P(D_i(1)=0,D_i(0)=1)}_{\text{defiers}}. \end{aligned} \]
That is, ITT is a mixture over the four potential groups.
We know that the ITT effect of \(Z_i\) on \(Y_i\) is zero for always-takers and never-takers due to the exclusion restriction, i.e., \(Z_i\) affects \(Y_i\) only through \(D_i\), and \(D_i\) does not vary with \(Z_i\) for always-takers and never-takers. Moreover, the monotonicity assumption rules out the existence of defiers. Hence, only compliers contribute to the effect of \(Z_i\) on \(Y_i\), then \(\mathbb{E}[Y_i(1,D_i(1))-Y_i(0,D_i(0))]\) is
\[ \begin{aligned} \mathbb{E}[Y_i(1,D_i(1)) - Y_i(0,D_i(0)) \mid D_i(1)=1, D_i(0)=0]\cdot P(D_i(1)=1, D_i(0)=0) \end{aligned} \]
For compliers, \(D_i = Z_i\), so we can simplify \(Y_i(1,D_i(1)) = Y_i(1,1) = Y_i(1)\) and \(Y_i(0,D_i(0)) = Y_i(0,0) = Y_i(0)\). Thus, \[ \mathbb{E}[Y_i(1) - Y_i(0)] = \mathbb{E}[Y_i(1) - Y_i(0) \mid D_i(1) = 1, D_i(0) = 0] \cdot P(D_i(1) = 1, D_i(0) = 0), \] which implies that \[ \tau_{LATE} = \mathbb{E}[Y_i(1) - Y_i(0) \mid D_i(1) = 1, D_i(0) = 0] = \frac{\mathbb{E}[Y_i(1) - Y_i(0)]}{P(D_i(1) = 1, D_i(0) = 0)}. \]
Under the assumption that the instrument \(Z_i\) is independent of the potential outcomes (i.e., marginal exchangeability), we have \[ \tau_{LATE} = \mathbb{E}[Y_i(1) - Y_i(0) \mid D_i(1) = 1, D_i(0) = 0] = \frac{\mathbb{E}[Y_i \mid Z_i = 1] - \mathbb{E}[Y_i \mid Z_i = 0]}{P(D_i(1) = 1, D_i(0) = 0)}. \]
We know that \[ P(D_i(1) = 1, D_i(0) = 0) = P(D_i = 1 \mid Z_i = 1) - P(D_i = 1 \mid Z_i = 0), \] and taking into account that \(\mathbb{E}[D_i \mid Z_i] = P(D_i = 1 \mid Z_i)\), we obtain \[ \tau_{LATE} = \frac{\mathbb{E}[Y_i \mid Z_i = 1] - \mathbb{E}[Y_i \mid Z_i = 0]}{\mathbb{E}[D_i \mid Z_i = 1] - \mathbb{E}[D_i \mid Z_i = 0]}. \]
This is the standard instrumental variables (IV) estimand, often referred to as the Wald estimator. Note that the relevance condition is required to ensure identification, i.e., \[ \mathbb{E}[D_i \mid Z_i = 1] - \mathbb{E}[D_i \mid Z_i = 0] \neq 0, \] that is, the instrument is strong enough that some units actually comply, there is a proportion of compliers in the population.
The IV estimand represents the ratio of the intention-to-treat effect on the outcome to the intention-to-treat effect on the treatment (i.e., the proportion of compliers). The instrument induces random variation in treatment: the numerator captures how outcomes respond to the instrument, and the denominator captures how treatment responds to the instrument. Dividing the two isolates the causal effect for compliers.
Note that the LATE is not the global average causal effect, and has been subject to several criticisms. First, the proportion of compliers in the population may be small, raising concerns about the policy relevance of this estimand. Observe that while we cannot identify all four principal strata (compliers, never-takers, always-takers, and defiers), the proportion of compliers is identifiable. Second, the monotonicity assumption is not always plausible, particularly in observational studies where instruments may induce heterogeneous behavioral responses. Third, partitioning the population into four strata can become ill-defined in settings where instruments arise from different mechanisms or individual-specific criteria (Deaton 2010; Hernán and Robins 2020). For arguments in defense of LATE against these critiques, see Angrist and Pischke (2010).
Example: A simple setting for point- and set-identified LATE
Assume we observe the following table.
| Type | \(Z_{obs}\) | \(D_{obs}\) | \(Y_{obs}\) | Units |
|---|---|---|---|---|
| Compliers, Never-takers | 0 | 0 | 3 | 50 |
| Never-takers | 1 | 0 | 4 | 20 |
| Compliers, Always-takers | 1 | 1 | 7 | 100 |
| Always-takers | 0 | 1 | 5 | 30 |
Let’s calculate the LATE assuming exclusion restrictions, and without assuming exclusion restrictions.
We first estimate the first stage and reduced form: \[ \mathbb{E}[D\mid Z=0]=\tfrac{30}{80}=0.37,\qquad \mathbb{E}[D\mid Z=1]=\tfrac{100}{120}\approx0.83, \] \[ \Delta_D=\mathbb{E}[D\mid Z=1]-\mathbb{E}[D\mid Z=0]\approx0.46. \]
\[ \mathbb{E}[Y\mid Z=0]=\tfrac{3\cdot 50+5\cdot 30}{80}=3.75,\qquad \mathbb{E}[Y\mid Z=1]=\tfrac{4\cdot 20+7\cdot 100}{120}=6.50, \] \[ \Delta_Y=\mathbb{E}[Y\mid Z=1]-\mathbb{E}[Y\mid Z=0]=2.75. \]
Compliance shares: \[ \eta_a=P(D=1\mid Z=0)=\tfrac{3}{8}=0.37,\quad \eta_c=\Delta_D=\tfrac{11}{24}\approx0.46,\quad \eta_n=1-\eta_a-\eta_c=\tfrac{1}{6}\approx0.17. \]
Then, we can point-identified the LATE under exclusion restriction, the Wald estimand gives \[ \text{LATE}=\frac{\Delta_Y}{\Delta_D}=\frac{2.75}{0.458}=6. \]
We achieved point identification by imposing the exclusion restriction, which requires that treatment assignment is unrelated to potential outcomes for never-takers and always-takers.75 This is, \[ \mathbb{E}[Y \mid Z=1, C=n] = \mathbb{E}[Y \mid Z=0, C=n], \] and \[ \mathbb{E}[Y \mid Z=1, C=a] = \mathbb{E}[Y \mid Z=0, C=a]. \]
Without exclusion restrictions, we should take into account that \[ \delta_n = \mathbb{E}[Y \mid Z=1, C=n] - \mathbb{E}[Y \mid Z=0, C=n] \neq 0, \] \[ \delta_a = \mathbb{E}[Y \mid Z=1, C=a] - \mathbb{E}[Y \mid Z=0, C=a] \neq 0. \]
Then \[ \Delta_Y = \eta_c \cdot \text{LATE} + \eta_n \delta_n + \eta_a \delta_a, \] so that \[ \text{LATE} = \frac{\Delta_Y - \eta_n \delta_n - \eta_a \delta_a}{\eta_c}. \]
From the table we know \[ \mathbb{E}[Y \mid Z=1, C=n] = 4, \quad \mathbb{E}[Y \mid Z=0, C=a] = 5. \]
We assume that the bounding outcomes come from the observed support \(Y \in [3,7]\). Then, \[ \delta_n \in [-3,1], \quad \delta_a \in [-2,2]. \]
Therefore, \[ \text{LATE}_{\min} = \frac{\Delta_Y - \eta_n \cdot 1 - \eta_a \cdot 2}{\eta_c} = 4, \]
\[ \text{LATE}_{\max} = \frac{\Delta_Y - \eta_n (-3) - \eta_a (-2)}{\eta_c} \approx 8.73. \]
Then, without exclusion restrictions the LATE is set identified, \(\text{LATE} \in [4, 8.73]\), and with exclusion restrictions, the LATE is point identified, \(\text{LATE} = 6\).
Example: Effects of vitamin A supplements on children’s survival
This example is taken from Guido W. Imbens and Rubin (1997). The authors perform Bayesian inference for causal effects in a completely randomized experiment with no covariates and partial compliance. The experiment was conducted in Indonesia, where children were randomly assigned to receive vitamin A supplements. No individual assigned to the control group (\(Z_i = 0\)) actually took the vitamin, meaning that \(D_i(0) = 1\) was never observed. This rules out always-takers and defiers. However, some individuals assigned to the treatment group (\(Z_i = 1\)) did not take the vitamin, so \(D_i(1) = 0\) occurred for some units. Consequently, \(D_i(1) \geq D_i(0)\) holds for all individuals (there are not defiers), satisfying the monotonicity assumption. Under this setting, the population consists only of compliers and never-takers.
| Type | Assignment \(Z_{\text{obs},i}\) | Treatment \(D_{\text{obs},i}\) | Survival \(Y_{\text{obs},i}\) | Units |
|---|---|---|---|---|
| Complier or never-taker | 0 | 0 | 0 | 74 |
| Complier or never-taker | 0 | 0 | 1 | 11,514 |
| Never-taker | 1 | 0 | 0 | 34 |
| Never-taker | 1 | 0 | 1 | 2,385 |
| Complier | 1 | 1 | 0 | 12 |
| Complier | 1 | 1 | 1 | 9,663 |
This table summarizes the data. Using this table, we can illustrate key concepts in the identification of causal effects with noncompliance. Let \(C_i\) denote the compliance type of individual \(i\), which in this case can be either a complier (\(c\)) or a never-taker (\(n\)). The probability of being a complier, \(\omega := P(C_i = c)\), is given by
\[ P(C_i = c) = \underbrace{P(D_i = 1 \mid Z_i = 1)}_{P(\text{compliers}) + P(\text{always-takers})} - \underbrace{P(D_i = 1 \mid Z_i = 0)}_{P(\text{always-takers}) = 0} = \frac{P(D_i = 1, Z_i = 1)}{P(Z_i = 1)}. \]
Thus, the ML estimate is
\[ \hat{\omega} = \frac{12 + 9{,}663}{12 + 9{,}663 + 34 + 2{,}385}= 0.8. \]
Note that \(P(C_i = n) = 1 - P(C_i = c)\) in this example; thus, the ML estimate is \(1-\hat{\omega} = 0.2\).
The probability of survival for compliers assigned to treatment, \(\eta_{c1} := P(Y_i = 1 \mid C_i = c, Z_i = 1)\), is
\[ P(Y_i = 1 \mid C_i = c, Z_i = 1) = \frac{P(Y_i = 1, C_i = c \mid Z_i = 1) \times P(Z_i = 1)}{P(C_i = c \mid Z_i = 1) \times P(Z_i = 1)}. \]
Thus, the ML estimate is \(\hat{\eta}_{c1}= \tfrac{9{,}663}{9{,}663 + 12}= 0.999.\)
Similarly, the probability of survival for never-takers assigned to treatment, \(\eta_{n1} := P(Y_i = 1 \mid C_i = n, Z_i = 1)\), is
\[ P(Y_i = 1 \mid C_i = n, Z_i = 1) = \frac{P(Y_i = 1, C_i = n \mid Z_i = 1) \times P(Z_i = 1)}{P(C_i = n \mid Z_i = 1) \times P(Z_i = 1)}. \]
Consequently, the ML estimate is \(\hat{\eta}_{n1} = \tfrac{2{,}385}{2{,}385 + 34} = 0.986.\)
Note that \(\eta_{c0} = P(Y_i = 1 \mid C_i = c, Z_i = 0)\) and \(\eta_{n0} = P(Y_i = 1 \mid C_i = n, Z_i = 0)\) cannot be point-identified. However, we can obtain set identification because
\[\begin{align*} \eta_0:=P(Y_i = 1 \mid Z_i = 0) &= P(Y_i = 1 \mid Z_i = 0, C_i = c) \times P(C_i = c) \\ &\quad + P(Y_i = 1 \mid Z_i = 0, C_i = n) \times P(C_i = n) \\ &= \frac{P(Y_i = 1, Z_i = 0)}{P(Z_i = 0)}, \end{align*}\]
where the ML estimate is \(\hat{\eta}_0= \tfrac{11{,}514}{11{,}514 + 74}= 0.9936.\)
The first equality holds because the probability of survival given no treatment assignment is expressed as a mixture by the law of total probability, and the second equality follows from Bayes’ rule.
This implies that
\[ 0.9936 = \hat{\omega} \hat{\eta}_{c0} + (1-\hat{\omega})\hat{\eta}_{n0}, \]
which leads to
\[ \hat{\eta}_{n0} = 4.968 - 4\hat{\eta}_{c0}. \]
Given that probabilities must lie in the unit interval, such that \(0 \leq 4.968 - 4\hat{\eta}_{c0} \leq 1\), we obtain:
(i) \(\hat{\eta}_{c0} \leq 1 \leq 1.242\) (automatically satisfied), and
(ii) \(4\hat{\eta}_{c0} \geq 4.968 - 1 = 3.968\), which implies \(\hat{\eta}_{c0} \geq 0.992\).
Consequently, the ML estimates are \(\hat{\eta}_{c0} \in [0.992, 1]\) and \(\hat{\eta}_{n0} \in [0.968, 1]\).
These results imply that the complier average causal effect (CACE) is
\[\begin{align*}
\tau_{CACE} &= \mathbb{E}[Y_i(1)-Y_i(0)\mid D_i(1)=1,D_i(0)=0] \\
&= P[Y_i = 1 \mid C_i = c, Z_i = 1] - P[Y_i = 1 \mid C_i = c, Z_i = 0] \\
&= \eta_{c1} - \eta_{c0},
\end{align*}\]
where the first line is the formal definition, the second equality uses random assignment to express the estimand in terms of observed probabilities, and the third relies on the model parameterization.
The CACE is only set-identified, yielding the interval
\[ \hat{\tau}_{CACE} \in [-0.001, 0.007], \]
meaning that the survival rate among compliers can vary between -1 and 7 per 1,000 children due to vitamin A supplementation.
Remember that point identification can be achieved by imposing the exclusion restriction, which requires that treatment assignment is unrelated to potential outcomes for never-takers and always-takers. Under this assumption,
\[ P(Y_i = y \mid C_i = n, Z_i = z) = P(Y_i = y \mid C_i = n), \]
so that \(\hat{\eta}_{n1} = \hat{\eta}_{n0} = \hat{\eta}_n = 0.986\). Substituting into the mixture equation yields \(\hat{\eta}_{c0} = 0.9955\), and consequently,
\[ \hat{\tau}_{CACE} = 0.0035, \]
indicating that survival increases by approximately 3.5 per 1,000 children due to vitamin A supplementation.76
We use conjugate families to perform Bayesian inference in this example. Specifically, we adopt the Bernoulli-Beta model (see Section 3.2) with independent non-informative Beta priors, each having parameters equal to 1. This corresponds to a uniform distribution on the interval \((0,1)\).
An advantage of the Bayesian formulation is that, after applying data augmentation with the compliance type \(C_i\), all the conditional posterior distributions are Beta (see Guido W. Imbens and Rubin (1997) for details in derivations). In particular:
\[ \omega \mid \mathbf{C}, \mathbf{Z}_{\text{obs}}, \mathbf{D}_{\text{obs}}, \mathbf{Y}_{\text{obs}} \sim \text{Beta}(1 + N_c,\, 1 + N_n), \]
where \(N_c\) and \(N_n\) denote the number of compliers and never-takers, respectively.
\[ \eta_{c1} \mid \mathbf{C}, \mathbf{Z}_{\text{obs}}, \mathbf{D}_{\text{obs}}, \mathbf{Y}_{\text{obs}} \sim \text{Beta}(1 + 9{,}663,\, 1 + 12), \]
\[ \eta_{n1} \mid \mathbf{C}, \mathbf{Z}_{\text{obs}}, \mathbf{D}_{\text{obs}}, \mathbf{Y}_{\text{obs}} \sim \text{Beta}(1 + 2{,}385,\, 1 + 34), \]
\[ \eta_{c0} \mid \mathbf{C}, \mathbf{Z}_{\text{obs}}, \mathbf{D}_{\text{obs}}, \mathbf{Y}_{\text{obs}} \sim \text{Beta}(1 + N_{c01},\, 1 + N_{c00}), \]
where \(N_{c01}\) and \(N_{c00}\) are the numbers of compliers in the control group who survived and did not survive, respectively.
\[ \eta_{n0} \mid \mathbf{C}, \mathbf{Z}_{\text{obs}}, \mathbf{D}_{\text{obs}}, \mathbf{Y}_{\text{obs}} \sim \text{Beta}(1 + N_{n01},\, 1 + N_{n00}), \]
where \(N_{n01}\) and \(N_{n00}\) are the numbers of never-takers in the control group who survived and did not survive, respectively.
In addition, the conditional probability of being a complier is given by:
\[ P(C_i = c \mid Z_{\text{obs},i}, D_{\text{obs},i}, Y_{\text{obs},i}) = \begin{cases} 0, & i \in \{Z_i = 1, D_i = 0\},\\ 1, & i \in \{Z_i = 1, D_i = 1\},\\ \dfrac{\omega g_{c0,i}}{\omega g_{c0,i} + (1-\omega) g_{n0,i}}, & i \in \{Z_i = 0\}, \end{cases} \]
where \(g_{c0,i} = \eta_{c0}^{Y_{\text{obs},i}} (1 - \eta_{c0})^{1 - Y_{\text{obs},i}}\) and \(g_{n0,i} = \eta_{n0}^{Y_{\text{obs},i}} (1 - \eta_{n0})^{1 - Y_{\text{obs},i}}\). Note that \(Y_{\text{obs},i} = 1\) implies \(g_{c0,i} = \eta_{c0}\) and \(g_{n0,i} = \eta_{n0}\), while \(Y_{\text{obs},i} = 0\) implies \(g_{c0,i} = (1 - \eta_{c0})\) and \(g_{n0,i} = (1 - \eta_{n0})\).
The following code shows the implementation, and the corresponding figure displays the posterior distribution of the CACE. The mean is 0.0024, and the 95% credible interval is (-0.0012, 0.0071).
We can perform inference by imposing the exclusion restriction, setting \(\eta_{n} = \eta_{n0} = \eta_{n1}\), so that the posterior distribution is
\[ \eta_{n} \mid \mathbf{C}, \mathbf{Z}_{\text{obs}}, \mathbf{D}_{\text{obs}}, \mathbf{Y}_{\text{obs}} \sim \text{Beta}(1 + N_{n1},\, 1 + N_{n0}), \]
where \(N_{n1}\) and \(N_{n0}\) denote the numbers of never-takers who survived and did not survive, respectively. This is the only modification to the Gibbs sampler.
The second part of the code shows the implementation, and the second figure displays the posterior distribution of the CACE (which equals the LATE under the exclusion restriction). The posterior mean is 0.0030, and the 95% credible interval is (0.0008, 0.0054). Therefore, imposing the exclusion restriction leaves the posterior mean approximately unchanged but increases the precision and informativeness of the posterior distribution. Without the restriction, the posterior was relatively flat within the 95% credible interval, whereas under the exclusion restriction, the posterior distribution is approximately normal, resulting in a narrower 95% credible interval.
rm(list = ls()); set.seed(10101)
library(dplyr)
# Simulate data
Nc111 <- 9663
c111 <- cbind(rep(1, Nc111), rep(1, Nc111), rep(1, Nc111))
Nc110 <- 12
c110 <- cbind(rep(1, Nc110), rep(1, Nc110), rep(0, Nc110))
Nn101 <- 2385
n101 <- cbind(rep(1, Nn101), rep(0, Nn101), rep(1, Nn101))
Nn100 <- 34
n100 <- cbind(rep(1, Nn100), rep(0, Nn100), rep(0, Nn100))
Ncn001 <- 11514
cn001 <- cbind(rep(0, Ncn001), rep(0, Ncn001), rep(1, Ncn001))
Ncn000 <- 74
cn000 <- cbind(rep(0, Ncn000), rep(0, Ncn000), rep(0, Ncn000))
mydata <- rbind(c111, c110, n101, n100, cn001, cn000)
mydata <- data.frame(Z = mydata[,1], D = mydata[,2], Y = mydata[,3])
N <- dim(mydata)[1]
attach(mydata)
# Sampling function C (type)
SampleType <- function(z, d, y, wc, nc0, nn0){
if(z == 1 & d == 0){
pc <- 0
}else{
if(z == 1 & d == 1){
pc <- 1
}else{
if(y == 1){
pc <- (wc * nc0) / (wc * nc0 + (1 - wc) * nn0)
}else{
pc <- (wc * (1 - nc0)) / (wc * (1 - nc0) + (1 - wc) * (1 - nn0))
}
}
}
rbinom(1, 1, prob = pc) # 1: Complier/ 0: Never taker
}
z = 0; d = 0; y = 0; wc = 0.8; nc0 = 0.9; nn0 = 0.05
SampleType(z = z, d = d, y = y, wc = wc, nc0 = nc0, nn0 = nn0)## [1] 0Clat <- sapply(1:N, function(i){SampleType(z = Z[i], d = D[i], y = Y[i], wc = wc, nc0 = nc0, nn0 = nn0)})
# Gibbs sampler
a0 <- 1; b0 <- 1 # Hyperparameters beta priors
burnin <- 500; S <- 2000; tot <- S + burnin
PosteriorDraws <- matrix(NA, tot, 5)
pb <- txtProgressBar(min = 0, max = tot, style = 3)## | | | 0%for(s in 1:tot){
dataLat <- cbind(mydata, Clat)
Nc011 <- sum(dataLat$Z == 0 & dataLat$Clat == 1 & dataLat$Y == 1)
Nc010 <- sum(dataLat$Z == 0 & dataLat$Clat == 1 & dataLat$Y == 0)
Nn001 <- sum(dataLat$Z == 0 & dataLat$Clat == 0 & dataLat$Y == 1)
Nn000 <- sum(dataLat$Z == 0 & dataLat$Clat == 0 & dataLat$Y == 0)
Nc <- sum(Clat == 1)
Nn <- sum(Clat == 0)
wc <- rbeta(1, 1 + Nc, 1 + Nn)
nc1 <- rbeta(1, 1 + Nc111, 1 + Nc110)
nn1 <- rbeta(1, 1 + Nn101, 1 + Nn100)
nc0 <- rbeta(1, 1 + Nc011, 1 + Nc010)
nn0 <- rbeta(1, 1 + Nn001, 1 + Nn000)
Clat <- sapply(1:N, function(i){SampleType(z = Z[i], d = D[i], y = Y[i], wc = wc, nc0 = nc0, nn0 = nn0)})
PosteriorDraws[s, ] <- c(wc, nc1, nc0, nn1, nn0)
setTxtProgressBar(pb, s)
}## | | | 1% | |= | 1% | |= | 2% | |== | 2% | |== | 3% | |== | 4% | |=== | 4% | |=== | 5% | |==== | 5% | |==== | 6% | |===== | 6% | |===== | 7% | |===== | 8% | |====== | 8% | |====== | 9% | |======= | 9% | |======= | 10% | |======= | 11% | |======== | 11% | |======== | 12% | |========= | 12% | |========= | 13% | |========= | 14% | |========== | 14% | |========== | 15% | |=========== | 15% | |=========== | 16% | |============ | 16% | |============ | 17% | |============ | 18% | |============= | 18% | |============= | 19% | |============== | 19% | |============== | 20% | |============== | 21% | |=============== | 21% | |=============== | 22% | |================ | 22% | |================ | 23% | |================ | 24% | |================= | 24% | |================= | 25% | |================== | 25% | |================== | 26% | |=================== | 26% | |=================== | 27% | |=================== | 28% | |==================== | 28% | |==================== | 29% | |===================== | 29% | |===================== | 30% | |===================== | 31% | |====================== | 31% | |====================== | 32% | |======================= | 32% | |======================= | 33% | |======================= | 34% | |======================== | 34% | |======================== | 35% | |========================= | 35% | |========================= | 36% | |========================== | 36% | |========================== | 37% | |========================== | 38% | |=========================== | 38% | |=========================== | 39% | |============================ | 39% | |============================ | 40% | |============================ | 41% | |============================= | 41% | |============================= | 42% | |============================== | 42% | |============================== | 43% | |============================== | 44% | |=============================== | 44% | |=============================== | 45% | |================================ | 45% | |================================ | 46% | |================================= | 46% | |================================= | 47% | |================================= | 48% | |================================== | 48% | |================================== | 49% | |=================================== | 49% | |=================================== | 50% | |=================================== | 51% | |==================================== | 51% | |==================================== | 52% | |===================================== | 52% | |===================================== | 53% | |===================================== | 54% | |====================================== | 54% | |====================================== | 55% | |======================================= | 55% | |======================================= | 56% | |======================================== | 56% | |======================================== | 57% | |======================================== | 58% | |========================================= | 58% | |========================================= | 59% | |========================================== | 59% | |========================================== | 60% | |========================================== | 61% | |=========================================== | 61% | |=========================================== | 62% | |============================================ | 62% | |============================================ | 63% | |============================================ | 64% | |============================================= | 64% | |============================================= | 65% | |============================================== | 65% | |============================================== | 66% | |=============================================== | 66% | |=============================================== | 67% | |=============================================== | 68% | |================================================ | 68% | |================================================ | 69% | |================================================= | 69% | |================================================= | 70% | |================================================= | 71% | |================================================== | 71% | |================================================== | 72% | |=================================================== | 72% | |=================================================== | 73% | |=================================================== | 74% | |==================================================== | 74% | |==================================================== | 75% | |===================================================== | 75% | |===================================================== | 76% | |====================================================== | 76% | |====================================================== | 77% | |====================================================== | 78% | |======================================================= | 78% | |======================================================= | 79% | |======================================================== | 79% | |======================================================== | 80% | |======================================================== | 81% | |========================================================= | 81% | |========================================================= | 82% | |========================================================== | 82% | |========================================================== | 83% | |========================================================== | 84% | |=========================================================== | 84% | |=========================================================== | 85% | |============================================================ | 85% | |============================================================ | 86% | |============================================================= | 86% | |============================================================= | 87% | |============================================================= | 88% | |============================================================== | 88% | |============================================================== | 89% | |=============================================================== | 89% | |=============================================================== | 90% | |=============================================================== | 91% | |================================================================ | 91% | |================================================================ | 92% | |================================================================= | 92% | |================================================================= | 93% | |================================================================= | 94% | |================================================================== | 94% | |================================================================== | 95% | |=================================================================== | 95% | |=================================================================== | 96% | |==================================================================== | 96% | |==================================================================== | 97% | |==================================================================== | 98% | |===================================================================== | 98% | |===================================================================== | 99% | |======================================================================| 99% | |======================================================================| 100%keep <- seq((burnin+1), tot)
LATE <- PosteriorDraws[keep, 2] - PosteriorDraws[keep, 3]
LATEmean <- mean(LATE)
LATEci <- quantile(LATE, c(0.025, 0.975))
# Plot posterior distribution of CATE
hist(LATE, breaks = 40, freq = FALSE,
main = "Posterior Distribution of CACE",
xlab = "CACE", col = "lightblue", border = "white")
abline(v = LATEmean, col = "red", lwd = 2)
abline(v = LATEci, col = "darkgreen", lty = 2, lwd = 2)
legend("topright", legend = c("Posterior Mean", "95% Credible Interval"),
col = c("red", "darkgreen"), lwd = 2, lty = c(1, 2),
bty = "n", cex = 0.8) # Smaller legend using cex######## Imposing exclusion restrictions #########
PosteriorDrawsER <- matrix(NA, tot, 4)
pb <- txtProgressBar(min = 0, max = tot, style = 3)## | | | 0%for(s in 1:tot){
dataLat <- cbind(mydata, Clat)
Nc011 <- sum(dataLat$Z == 0 & dataLat$Clat == 1 & dataLat$Y == 1)
Nc010 <- sum(dataLat$Z == 0 & dataLat$Clat == 1 & dataLat$Y == 0)
Nn01 <- sum(dataLat$Clat == 0 & dataLat$Y == 1)
Nn00 <- sum(dataLat$Clat == 0 & dataLat$Y == 0)
Nc <- sum(Clat == 1)
Nn <- sum(Clat == 0)
wc <- rbeta(1, 1 + Nc, 1 + Nn)
nc1 <- rbeta(1, 1 + Nc111, 1 + Nc110)
nn <- rbeta(1, 1 + Nn01, 1 + Nn00)
nc0 <- rbeta(1, 1 + Nc011, 1 + Nc010)
Clat <- sapply(1:N, function(i){SampleType(z = Z[i], d = D[i], y = Y[i], wc = wc, nc0 = nc0, nn0 = nn)})
PosteriorDrawsER[s, ] <- c(wc, nc1, nc0, nn)
setTxtProgressBar(pb, s)
}## | | | 1% | |= | 1% | |= | 2% | |== | 2% | |== | 3% | |== | 4% | |=== | 4% | |=== | 5% | |==== | 5% | |==== | 6% | |===== | 6% | |===== | 7% | |===== | 8% | |====== | 8% | |====== | 9% | |======= | 9% | |======= | 10% | |======= | 11% | |======== | 11% | |======== | 12% | |========= | 12% | |========= | 13% | |========= | 14% | |========== | 14% | |========== | 15% | |=========== | 15% | |=========== | 16% | |============ | 16% | |============ | 17% | |============ | 18% | |============= | 18% | |============= | 19% | |============== | 19% | |============== | 20% | |============== | 21% | |=============== | 21% | |=============== | 22% | |================ | 22% | |================ | 23% | |================ | 24% | |================= | 24% | |================= | 25% | |================== | 25% | |================== | 26% | |=================== | 26% | |=================== | 27% | |=================== | 28% | |==================== | 28% | |==================== | 29% | |===================== | 29% | |===================== | 30% | |===================== | 31% | |====================== | 31% | |====================== | 32% | |======================= | 32% | |======================= | 33% | |======================= | 34% | |======================== | 34% | |======================== | 35% | |========================= | 35% | |========================= | 36% | |========================== | 36% | |========================== | 37% | |========================== | 38% | |=========================== | 38% | |=========================== | 39% | |============================ | 39% | |============================ | 40% | |============================ | 41% | |============================= | 41% | |============================= | 42% | |============================== | 42% | |============================== | 43% | |============================== | 44% | |=============================== | 44% | |=============================== | 45% | |================================ | 45% | |================================ | 46% | |================================= | 46% | |================================= | 47% | |================================= | 48% | |================================== | 48% | |================================== | 49% | |=================================== | 49% | |=================================== | 50% | |=================================== | 51% | |==================================== | 51% | |==================================== | 52% | |===================================== | 52% | |===================================== | 53% | |===================================== | 54% | |====================================== | 54% | |====================================== | 55% | |======================================= | 55% | |======================================= | 56% | |======================================== | 56% | |======================================== | 57% | |======================================== | 58% | |========================================= | 58% | |========================================= | 59% | |========================================== | 59% | |========================================== | 60% | |========================================== | 61% | |=========================================== | 61% | |=========================================== | 62% | |============================================ | 62% | |============================================ | 63% | |============================================ | 64% | |============================================= | 64% | |============================================= | 65% | |============================================== | 65% | |============================================== | 66% | |=============================================== | 66% | |=============================================== | 67% | |=============================================== | 68% | |================================================ | 68% | |================================================ | 69% | |================================================= | 69% | |================================================= | 70% | |================================================= | 71% | |================================================== | 71% | |================================================== | 72% | |=================================================== | 72% | |=================================================== | 73% | |=================================================== | 74% | |==================================================== | 74% | |==================================================== | 75% | |===================================================== | 75% | |===================================================== | 76% | |====================================================== | 76% | |====================================================== | 77% | |====================================================== | 78% | |======================================================= | 78% | |======================================================= | 79% | |======================================================== | 79% | |======================================================== | 80% | |======================================================== | 81% | |========================================================= | 81% | |========================================================= | 82% | |========================================================== | 82% | |========================================================== | 83% | |========================================================== | 84% | |=========================================================== | 84% | |=========================================================== | 85% | |============================================================ | 85% | |============================================================ | 86% | |============================================================= | 86% | |============================================================= | 87% | |============================================================= | 88% | |============================================================== | 88% | |============================================================== | 89% | |=============================================================== | 89% | |=============================================================== | 90% | |=============================================================== | 91% | |================================================================ | 91% | |================================================================ | 92% | |================================================================= | 92% | |================================================================= | 93% | |================================================================= | 94% | |================================================================== | 94% | |================================================================== | 95% | |=================================================================== | 95% | |=================================================================== | 96% | |==================================================================== | 96% | |==================================================================== | 97% | |==================================================================== | 98% | |===================================================================== | 98% | |===================================================================== | 99% | |======================================================================| 99% | |======================================================================| 100%keep <- seq((burnin+1), tot)
LATEER <- PosteriorDrawsER[keep, 2] - PosteriorDrawsER[keep, 3]
LATEERmean <- mean(LATEER)
LATEERci <- quantile(LATEER, c(0.025, 0.975))
# Plot posterior distribution of LATE
hist(LATEER, breaks = 40, freq = FALSE, main = "Posterior Distribution of LATE: Exclusion restrictions", xlab = "LATE", col = "lightblue", border = "white")
abline(v = LATEERmean, col = "red", lwd = 2)
abline(v = LATEERci, col = "darkgreen", lty = 2, lwd = 2)
legend("topright", legend = c("Posterior Mean", "95% Credible Interval"), col = c("red", "darkgreen"), lwd = 2, lty = c(1, 2), bty = "n", cex = 0.8)This example illustrates how the Bayesian framework provides a way to quantify uncertainty and conduct sensitivity analysis regarding the exclusion restriction. See Hirano et al. (2000) for an extension controlling for covariates.
In addition, it is worth mentioning that in partially identified models, the asymptotic equivalence between Bayesian and Frequentist inference breaks down. In particular, credible sets for partially identified parameters tend to be smaller than confidence sets asymptotically (Moon and Schorfheide 2012). This occurs because the posterior remains asymptotically sensitive to the prior, and Bayesian credible sets lie strictly inside the true identified set. To address this disagreement, Giacomini and Kitagawa (2021) propose a multi-prior robust Bayesian approach that helps reconcile Bayesian and Frequentist inference in set-identified models, which are a special case of partially identified models.
Example: Treatment effect of 401(k) participation on net financial assets
In the example of the effect of eligibility on 401(k) on net financial assets, we calculate the ITT effect. Now, following Victor Chernozhukov and Hansen (2004), we use eligibility as an instrument for participation and perform inference on the (local) average treatment effect. We adopt the framework described in Section 7.3 for this example. The following code illustrates the procedure, and the figure displays the posterior distribution of the (local) average treatment effect of participation. The 95% credible interval is (USD 5,102, USD 12,010), and the posterior mean is USD 8,520, which is higher than the intention-to-treat effect associated with eligibility (USD 5,903).
Exercise 6 asks how to recover the ITT from the LATE and the effect of eligibility on participation. See T. Conley, Hansen, and Rossi (2012) for practical methods to conduct sensitivity analysis of posterior results when relaxing the exclusion restriction in IV settings. In addition, T. G. Conley et al. (2008) present a Bayesian inferential framework using a semi-parametric approach in which stochastic errors are modeled using a Dirichlet process (see Exercise 7), and Ramı́rez–Hassan and López-Vera (2024) extend this approach to systems of equations.
rm(list = ls()); set.seed(10101)
library(coda); library(ggplot2)
mydata <- read.csv("https://raw.githubusercontent.com/BEsmarter-consultancy/BSTApp/refs/heads/master/DataApp/401k.csv", sep = ",", header = TRUE, quote = "")
# Attach variables
attach(mydata)## The following objects are masked from mydata (pos = 4):
##
## a1, a2, a3, a4, a401, a5, age, col, db, dum91, e401, ecat, educ,
## fsize, hequity, hmort, hown, hs, hval, i1, i2, i3, i4, i5, i6, i7,
## icat, inc, ira, male, marr, net_n401, net_nifa, net_tfa, nifa,
## nohs, p401, pira, smcol, tfa, tfa_he, tw, twoearn, X, zhat## The following object is masked from DataIntRate (pos = 30):
##
## i3## The following object is masked from DataIntRate (pos = 32):
##
## i3y <- net_tfa/1000 # Outcome: net financial assets
x <- as.vector(p401) # Endogenous regressor: participation
w <- as.matrix(cbind(1, age, inc, fsize, educ, marr, twoearn, db, pira, hown)) # Exogenous regressors with intercept
z <- as.matrix(e401) # Instrument: eligibility (NO intercept here)
X <- cbind(x, w); Z <- cbind(z, w)
# Dimensions
k <- ncol(X); kz <- ncol(Z)
# Priors
b0 <- rep(0, k); B0i <- diag(1e-5, k)
g0 <- rep(0, kz); G0i <- diag(1e-5, kz)
nu <- 3; Psi0 <- nu * 1000 * diag(2); Psi0i <- solve(Psi0)
# MCMC parameters
mcmc <- 5000; burnin <- 1000
tot <- mcmc + burnin; thin <- 1
# Auxiliary elements
XtX <- t(X)%*%X; ZtZ <- t(Z)%*%Z; nun <- nu + length(y)
# Gibbs sampling
PostBeta <- function(Sigma, Gamma){
w1 <- Sigma[1,1] - Sigma[1,2]^2/Sigma[2,2]
Bn <- solve(w1^(-1)*XtX + B0i)
yaux <- y - (Sigma[1,2]/Sigma[2,2])*(x - Z%*%Gamma)
bn <- Bn%*%(B0i%*%b0 + w1^(-1)*t(X)%*%yaux)
Beta <- MASS::mvrnorm(1, bn, Bn)
return(Beta)
}
PostGamma <- function(Sigma, Beta){
w2 <- Sigma[2,2] - Sigma[1,2]^2/Sigma[1,1]
Gn <- solve(w2^(-1)*ZtZ + G0i)
xaux <- x - (Sigma[1,2]/Sigma[1,1])*(y - X%*%Beta)
gn <- Gn%*%(G0i%*%g0 + w2^(-1)*t(Z)%*%xaux)
Gamma <- MASS::mvrnorm(1, gn, Gn)
return(Gamma)
}
PostSigma <- function(Beta, Gamma){
Uy <- y - X%*%Beta; Ux <- x - Z%*%Gamma
U <- cbind(Uy, Ux)
Psin <- solve(Psi0i + t(U)%*%U)
Sigmai <- rWishart::rWishart(1, df = nun, Sigma = Psin)
Sigma <- solve(Sigmai[,,1])
return(Sigma)
}
PostBetas <- matrix(0, tot, k)
PostGammas <- matrix(0, tot, kz)
PostSigmas <- matrix(0, tot, 2*(2+1)/2)
Beta <- rep(0, k); Gamma <- rep(0, kz)
pb <- txtProgressBar(min = 0, max = tot, style = 3)## | | | 0%for(s in 1:tot){
Sigma <- PostSigma(Beta = Beta, Gamma = Gamma)
Beta <- PostBeta(Sigma = Sigma, Gamma = Gamma)
Gamma <- PostGamma(Sigma = Sigma, Beta = Beta)
PostBetas[s,] <- Beta
PostGammas[s,] <- Gamma
PostSigmas[s,] <- matrixcalc::vech(Sigma)
setTxtProgressBar(pb, s)
}## | | | 1% | |= | 1% | |= | 2% | |== | 2% | |== | 3% | |== | 4% | |=== | 4% | |=== | 5% | |==== | 5% | |==== | 6% | |===== | 6% | |===== | 7% | |===== | 8% | |====== | 8% | |====== | 9% | |======= | 9% | |======= | 10% | |======= | 11% | |======== | 11% | |======== | 12% | |========= | 12% | |========= | 13% | |========= | 14% | |========== | 14% | |========== | 15% | |=========== | 15% | |=========== | 16% | |============ | 16% | |============ | 17% | |============ | 18% | |============= | 18% | |============= | 19% | |============== | 19% | |============== | 20% | |============== | 21% | |=============== | 21% | |=============== | 22% | |================ | 22% | |================ | 23% | |================ | 24% | |================= | 24% | |================= | 25% | |================== | 25% | |================== | 26% | |=================== | 26% | |=================== | 27% | |=================== | 28% | |==================== | 28% | |==================== | 29% | |===================== | 29% | |===================== | 30% | |===================== | 31% | |====================== | 31% | |====================== | 32% | |======================= | 32% | |======================= | 33% | |======================= | 34% | |======================== | 34% | |======================== | 35% | |========================= | 35% | |========================= | 36% | |========================== | 36% | |========================== | 37% | |========================== | 38% | |=========================== | 38% | |=========================== | 39% | |============================ | 39% | |============================ | 40% | |============================ | 41% | |============================= | 41% | |============================= | 42% | |============================== | 42% | |============================== | 43% | |============================== | 44% | |=============================== | 44% | |=============================== | 45% | |================================ | 45% | |================================ | 46% | |================================= | 46% | |================================= | 47% | |================================= | 48% | |================================== | 48% | |================================== | 49% | |=================================== | 49% | |=================================== | 50% | |=================================== | 51% | |==================================== | 51% | |==================================== | 52% | |===================================== | 52% | |===================================== | 53% | |===================================== | 54% | |====================================== | 54% | |====================================== | 55% | |======================================= | 55% | |======================================= | 56% | |======================================== | 56% | |======================================== | 57% | |======================================== | 58% | |========================================= | 58% | |========================================= | 59% | |========================================== | 59% | |========================================== | 60% | |========================================== | 61% | |=========================================== | 61% | |=========================================== | 62% | |============================================ | 62% | |============================================ | 63% | |============================================ | 64% | |============================================= | 64% | |============================================= | 65% | |============================================== | 65% | |============================================== | 66% | |=============================================== | 66% | |=============================================== | 67% | |=============================================== | 68% | |================================================ | 68% | |================================================ | 69% | |================================================= | 69% | |================================================= | 70% | |================================================= | 71% | |================================================== | 71% | |================================================== | 72% | |=================================================== | 72% | |=================================================== | 73% | |=================================================== | 74% | |==================================================== | 74% | |==================================================== | 75% | |===================================================== | 75% | |===================================================== | 76% | |====================================================== | 76% | |====================================================== | 77% | |====================================================== | 78% | |======================================================= | 78% | |======================================================= | 79% | |======================================================== | 79% | |======================================================== | 80% | |======================================================== | 81% | |========================================================= | 81% | |========================================================= | 82% | |========================================================== | 82% | |========================================================== | 83% | |========================================================== | 84% | |=========================================================== | 84% | |=========================================================== | 85% | |============================================================ | 85% | |============================================================ | 86% | |============================================================= | 86% | |============================================================= | 87% | |============================================================= | 88% | |============================================================== | 88% | |============================================================== | 89% | |=============================================================== | 89% | |=============================================================== | 90% | |=============================================================== | 91% | |================================================================ | 91% | |================================================================ | 92% | |================================================================= | 92% | |================================================================= | 93% | |================================================================= | 94% | |================================================================== | 94% | |================================================================== | 95% | |=================================================================== | 95% | |=================================================================== | 96% | |==================================================================== | 96% | |==================================================================== | 97% | |==================================================================== | 98% | |===================================================================== | 98% | |===================================================================== | 99% | |======================================================================| 99% | |======================================================================| 100%keep <- seq((burnin+1), tot, thin)
Bs <- PostBetas[keep,]
Gs <- PostGammas[keep,]
Sigmas <- PostSigmas[keep,]
summary(coda::mcmc(Bs))##
## Iterations = 1:5000
## Thinning interval = 1
## Number of chains = 1
## Sample size per chain = 5000
##
## 1. Empirical mean and standard deviation for each variable,
## plus standard error of the mean:
##
## Mean SD Naive SE Time-series SE
## [1,] 8.538e+00 1.7723708 2.507e-02 4.067e-02
## [2,] -3.325e+01 4.2945590 6.073e-02 6.073e-02
## [3,] 6.312e-01 0.0590983 8.358e-04 8.358e-04
## [4,] 9.267e-04 0.0000306 4.327e-07 4.327e-07
## [5,] -1.007e+00 0.4519552 6.392e-03 6.392e-03
## [6,] -6.140e-01 0.2286958 3.234e-03 3.234e-03
## [7,] 8.638e-01 1.7825719 2.521e-02 2.598e-02
## [8,] -1.930e+01 1.5737223 2.226e-02 2.456e-02
## [9,] -4.559e+00 1.3403824 1.896e-02 1.896e-02
## [10,] 2.913e+01 1.4713375 2.081e-02 2.081e-02
## [11,] 1.086e+00 1.3292147 1.880e-02 1.880e-02
##
## 2. Quantiles for each variable:
##
## 2.5% 25% 50% 75% 97.5%
## var1 5.104e+00 7.341e+00 8.530e+00 9.703e+00 1.210e+01
## var2 -4.165e+01 -3.624e+01 -3.325e+01 -3.031e+01 -2.490e+01
## var3 5.164e-01 5.913e-01 6.316e-01 6.713e-01 7.485e-01
## var4 8.665e-04 9.056e-04 9.268e-04 9.474e-04 9.867e-04
## var5 -1.898e+00 -1.310e+00 -1.001e+00 -7.042e-01 -1.286e-01
## var6 -1.066e+00 -7.741e-01 -6.120e-01 -4.576e-01 -1.754e-01
## var7 -2.640e+00 -3.422e-01 9.001e-01 2.050e+00 4.297e+00
## var8 -2.236e+01 -2.038e+01 -1.929e+01 -1.823e+01 -1.626e+01
## var9 -7.138e+00 -5.451e+00 -4.571e+00 -3.664e+00 -1.905e+00
## var10 2.623e+01 2.812e+01 2.913e+01 3.017e+01 3.190e+01
## var11 -1.545e+00 1.855e-01 1.082e+00 1.982e+00 3.701e+00##
## Iterations = 1:5000
## Thinning interval = 1
## Number of chains = 1
## Sample size per chain = 5000
##
## 1. Empirical mean and standard deviation for each variable,
## plus standard error of the mean:
##
## Mean SD Naive SE Time-series SE
## [1,] 6.934e-01 6.156e-03 8.707e-05 8.707e-05
## [2,] 2.892e-02 2.138e-02 3.023e-04 3.023e-04
## [3,] -6.962e-04 2.929e-04 4.143e-06 4.143e-06
## [4,] 1.073e-06 1.494e-07 2.113e-09 2.113e-09
## [5,] -4.529e-04 2.209e-03 3.124e-05 3.124e-05
## [6,] -2.613e-03 1.144e-03 1.617e-05 1.617e-05
## [7,] -1.775e-02 8.858e-03 1.253e-04 1.253e-04
## [8,] 6.188e-03 7.727e-03 1.093e-04 1.093e-04
## [9,] -4.132e-02 6.694e-03 9.467e-05 9.467e-05
## [10,] 4.922e-02 7.298e-03 1.032e-04 1.032e-04
## [11,] 1.163e-02 6.475e-03 9.157e-05 9.157e-05
##
## 2. Quantiles for each variable:
##
## 2.5% 25% 50% 75% 97.5%
## var1 6.812e-01 6.892e-01 6.934e-01 6.974e-01 7.054e-01
## var2 -1.279e-02 1.477e-02 2.887e-02 4.322e-02 7.058e-02
## var3 -1.275e-03 -8.914e-04 -6.974e-04 -4.970e-04 -1.210e-04
## var4 7.809e-07 9.729e-07 1.073e-06 1.173e-06 1.363e-06
## var5 -4.697e-03 -1.931e-03 -4.722e-04 1.036e-03 3.945e-03
## var6 -4.820e-03 -3.391e-03 -2.623e-03 -1.837e-03 -3.586e-04
## var7 -3.528e-02 -2.371e-02 -1.759e-02 -1.175e-02 -8.148e-04
## var8 -8.922e-03 9.215e-04 6.250e-03 1.140e-02 2.139e-02
## var9 -5.465e-02 -4.573e-02 -4.134e-02 -3.675e-02 -2.823e-02
## var10 3.473e-02 4.435e-02 4.926e-02 5.423e-02 6.340e-02
## var11 -9.920e-04 7.370e-03 1.167e-02 1.596e-02 2.421e-02##
## Iterations = 1:5000
## Thinning interval = 1
## Number of chains = 1
## Sample size per chain = 5000
##
## 1. Empirical mean and standard deviation for each variable,
## plus standard error of the mean:
##
## Mean SD Naive SE Time-series SE
## [1,] 3.091e+03 44.19352 6.250e-01 6.250e-01
## [2,] 5.307e-01 0.20303 2.871e-03 4.983e-03
## [3,] 7.588e-02 0.00108 1.527e-05 1.527e-05
##
## 2. Quantiles for each variable:
##
## 2.5% 25% 50% 75% 97.5%
## var1 3.006e+03 3.061e+03 3.090e+03 3120.5334 3.179e+03
## var2 1.215e-01 3.978e-01 5.271e-01 0.6687 9.293e-01
## var3 7.382e-02 7.516e-02 7.588e-02 0.0766 7.804e-02# Extract posterior draws for the treatment effect (participation = p401)
beta_draws <- Bs[,1]
# Plot posterior distribution of treatment effect
df_beta <- data.frame(effect = as.vector(beta_draws))
ggplot(df_beta, aes(x = effect)) + geom_density(fill = "steelblue", alpha = 0.6) +
geom_vline(xintercept = mean(beta_draws), color = "red", linetype = "dashed", linewidth = 1) + labs( title = "Posterior Distribution of 401(k) Participation Effect", x = expression(beta["p401"]), y = "Density") + theme_minimal(base_size = 14)References
Note that under monotonicity, defiers are ruled out, whereas for compliers, the exclusion restriction is not a separate assumption: by construction, their potential outcomes are indexed only by treatment status, since the instrument deterministically shifts them between \(D_i=0\) and \(D_i=1\). Thus, the exclusion restriction applies only to never-takers and always-takers, whose treatment status does not vary with the instrument.↩︎
CACE and LATE refer to the same estimand —the average causal effect for compliers— under monotonicity and the exclusion restriction. If the exclusion restriction fails, they differ because LATE (as identified by IV) no longer equals the complier-specific causal effect (CACE).↩︎