9.2 Missing data mechanism
Missing data mechanisms are typically classified as one of the following (Rubin 1976):
- MCAR: Missing completely at random,
- MAR: Missing at random, or
- MNAR: Missing not at random.
Missing data are MCAR if the probability of missingness is independent of the data. In other words, the data are MCAR if the reason for missing values in the outcome or predictors has nothing to do with the data values themselves, whether observed or missing. Missing data are MAR if the probability of missingness is independent of the missing values given the observed data. In other words, under MAR how likely a value is to be missing can be estimated based on the non-missing data. Missing data are MNAR if, even given all the observed information, the probability of missingness depends on the unobserved missing values themselves.
To illustrate the difference between these three missing data mechanisms, consider a dataset with the following three variables: disease status, level of exposure, and age. Suppose, for some individuals, exposure is missing (they do have an exposure value, but we do not know what it is). What do each of the three missing data mechanisms imply in this setting?
- MCAR: Any two individuals, regardless of their values of disease status, level of exposure, and age, have the same probability of having a missing value for exposure.
- MAR: Any two individuals with the same disease status and age have the same chance of having a missing exposure value, regardless of how large or small their actual level of exposure.
- MNAR: Even among individuals with the same disease status and age, the chance of having a missing exposure value depends on the level of exposure.
MCAR is generally unrealistic. Individuals who skip a question or refuse to be measured may be very different than those who comply, and they may have systematically different outcome and/or predictor values. MAR is at least somewhat plausible – it allows for systematic differences, as long as those differences are predictable based on observed information. Under MAR (and another condition called ignorability that is beyond the scope of this text), MI leads to consistent estimates with correct standard errors.
MNAR is often plausible, as well, but is more complicated to handle since the distinction between MAR and MNAR depends on unknown information. As a result, a common approach is to assume the data are MAR and use MI to handle the missing data. The plausibility of MAR is improved by including in the imputation model any variable that could be related to the chance of missingness. Evaluating the potential impact of a violation of the MAR assumption (in other words, MNAR) involves using advanced methods to posit a missing data model that depends on the unknown information. This model, by necessity, requires strong assumptions, so MNAR analyses typically include a sensitivity analysis in which the assumptions are varied, resulting in a range of possible conclusions (van Buuren 2018; Vink and van Buuren 2022).
When the data are MCAR, a complete case analysis will yield unbiased estimates, although MI will be more efficient in that the effective sample size will increase since no cases need to be discarded. Under MAR and MNAR, however, a complete case analysis will typically yield biased estimates. MI, however, can provide consistent estimates under MAR (assuming the imputation model does not leave out important variables and is correctly specified), but not under MNAR. These differences are illustrated in Figure 9.1, which is explained in the following.
In Chapter 6, our 2019 NSDUH teaching dataset was used to estimate the adjusted odds ratio (AOR) assessing the association between age of first alcohol use and lifetime marijuana use, adjusted for age, sex, and income. Figure 9.1 displays the results of the following simulation steps:
- Create a “no missing data” dataset: Remove all individuals with a missing age of first alcohol use. These individuals never used alcohol, so we do not want to impute ages for them. There were no other missing values in the dataset for the variables of interest.
- Create a MCAR dataset: Randomly set about 5% of each variable’s values to missing, independent of any of the data values.
- Create a MAR dataset: Randomly set each variable’s values to missing with a probability of missingness that depends on the values of all the other variables, but not that variable.
- Create a MNAR dataset: Randomly set each variable’s values to missing with a probability of missingness that depends on the values of all the variables, including that variable.
- For each of the three datasets that have missing values, estimate the regression coefficient for each term in the model using a complete case analysis and using MI. Within each of these six analyses, average over 25 runs of the simulation, and then exponentiate the average to obtain the estimated AOR for each term.
- Plot the AORs for each missing data analysis vs. the AORs from the “no missing data” dataset analysis.
The top left panel in Figure 9.1 illustrates that if the missing data are MCAR a complete case analysis results in unbiased estimates (this is a simulation with 25 iterations, so the points have some variation about the 45-degree line of equivalence just due to random noise). MI is consistent under MCAR, as shown in the top right panel, with the benefit of improved precision (not shown). The middle row illustrates that under MAR a complete case analysis yields biased estimates (the points are not on the line), but MI yields consistent estimates. The bottom row illustrates that, under MNAR, while MI reduces the bias found in a complete case analysis, it does not eliminate it.
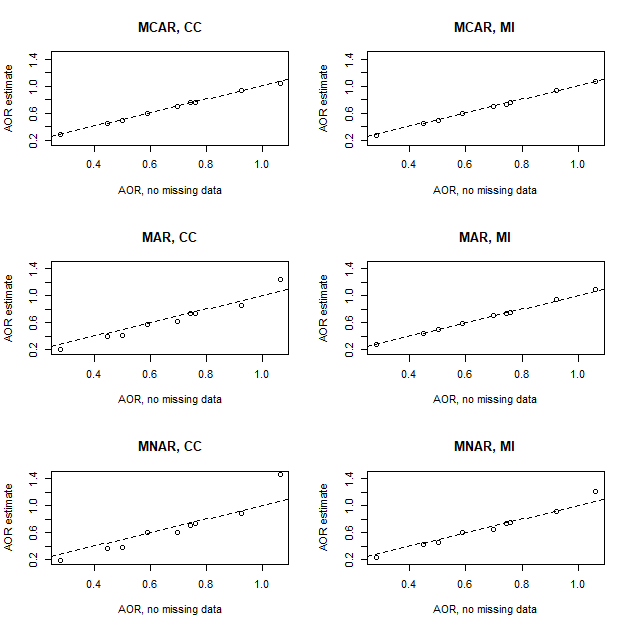
Figure 9.1: Bias in adjusted odds ratios (AORs) estimated using complete case analysis (CC) and multiple imputation (MI) under MCAR, MAR, and MNAR missing data mechanisms