7.2 Censoring
An event time \(T\) is censored if it is not known exactly but is known to be in some range. Three kinds of censored times are:
- Right-censored: \(T > t\). The event has not yet occurred as of time \(t\) and may never occur.
- Left-censored: \(T < t\). The event occurred before time \(t\).
- Interval-censored: \(t_1 < T < t_2\). The event occurred between times \(t_1\) and \(t_2\).
In this text, we will only consider right-censored event times.
Example 7.1: Figure 7.1 illustrates censoring for 6 of 2000 individuals from the 2019 US Natality data teaching dataset. As described in Appendix A.3, gestational ages >37 weeks were censored at 37 weeks (as in Michalowicz et al. (2006)) and a random subset of gestational ages were censored at times <37 weeks. Preterm birth times are denoted by solid circles, and censored times are denoted by open circles. Thirty-seven weeks is denoted by the vertical dashed line. Individuals 1, 3, and 5 experienced a preterm birth. Individual 2 was lost to follow-up at gestational age 20 weeks, so their event time is censored at 20 – all we know is that if this pregnancy ended in a preterm birth, it did so after 20 weeks. Individuals 4 and 6 had not yet given birth as of 37 weeks, so they, too, have censored event times (at 37 weeks).
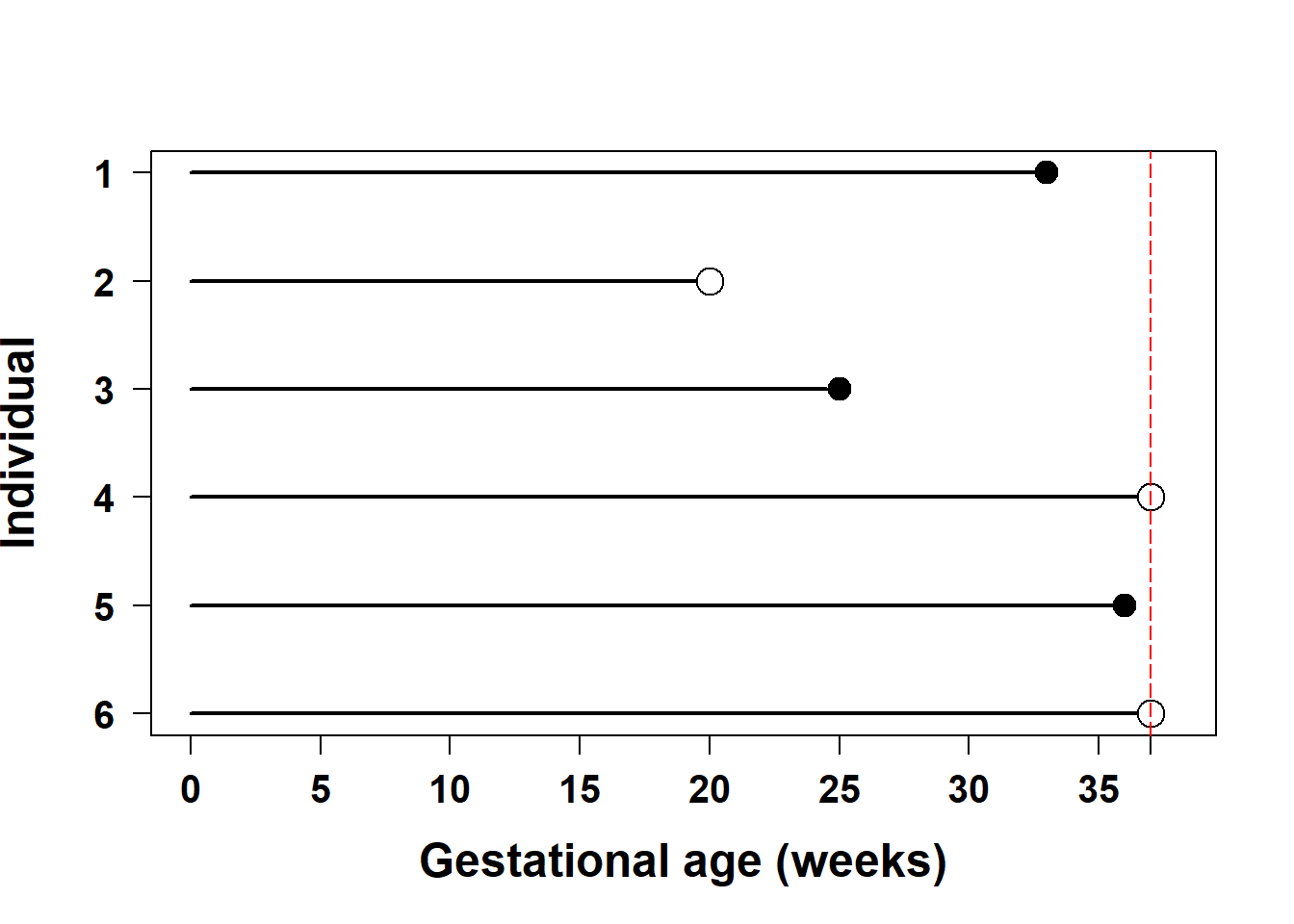
Figure 7.1: Censored and non-censored event times
There are multiple mechanisms that generate censored data:
- Type I censoring: The end of study time is pre-specified, making the censoring time(s) known before any data are collected.
- Type II censoring: The number of events is pre-specified. Thus, the end of study time and censoring time(s) are not known until after the data have been collected.
- Random censoring: The censoring times are not under the researcher’s control.
In the studies listed above, all of which have right-censored event times, the censoring is a mix of Type I and random. Each had a specific end time (e.g., 37 weeks for the preterm birth study; 36-month interview for the transition to heroin study), but some times were censored for other, random, reasons (e.g., loss to follow-up).
NOTE: Even with a known end of study time resulting in Type I censoring, the end-of-study censoring time may vary between individuals. For example, in the transition to heroin study, once the first interview was completed, everyone’s time from origin to end of study was known but, since not everyone began using pain pills at the same time, those times varied between participants.
7.2.1 Non-informative censoring assumption
The methods we will discuss assume that censoring is non-informative. Consider two individuals with the same risk factors, neither of whom have experienced the event of interest as of time \(t\). One is lost to follow-up at that time (and so their event time is right-censored at \(t\)) and the other continues in the study. Assuming non-informative censoring means that we assume these two individuals have the same subsequent risk of experiencing the event – knowing that one of them has a censored time does not add any information.
For example, consider a study of an intervention (vs. control) intended to increase survival after cancer surgery. The study runs for 1 year, and patients who survive to the end of the study have a survival time that is right-censored at 1 year. The fact that these times are censored does not give you any information about these patients’ subsequent likelihood of survival – the censoring had nothing to do with their condition other than the fact they survived to 1 year. Therefore, the censoring is non-informative. Suppose, instead, that an individual drops out of the study earlier than 1 year because they are not doing well. This individual may be less likely to survive than an individual who continued in the study beyond that time. Therefore, their censoring is informative. In this case, assuming non-informative censoring would lead to a biased assessment of the intervention. Censoring of individuals who drop out of the study early because they moved to another city where follow-up was not possible, however, would be non-informative (assuming the move had nothing to do with how well they were doing).