7.4 Hazard function

The cumulative risk of an event is the probability that the event occurs within a specified time period. The instantaneous risk of an event is known as the hazard of the event. In survival analysis, we are interested in how the hazard changes over time, how it differs between groups, and how it depends on risk factors. The hazard function \(h()\) at time \(t\) is defined mathematically as follows.

\[\begin{equation} h(t) = \lim_{\Delta t \to 0} \frac{P \left( t \leq T < t + \Delta t \vert T \geq t \right)}{\Delta t} \tag{7.1} \end{equation}\]

Equation (7.1) describes the following process: given that a person has not yet experienced the event prior to time \(t\) (the \(\vert T \geq t\) part of the numerator), compute the probability of the event occurring in a subsequent time window starting at \(t\) (the \(t \leq T < t + \Delta t\) part of the numerator) per unit time (the \(\Delta t\) in the denominator) and then shrink the length of the time window to zero (\(\lim_{\Delta t \to 0}\)). Thus, the hazard function at time \(t\) is the instantaneous risk of experiencing the event among those who are still at risk. The hazard function is sometimes referred to as the hazard rate.

Example 7.1 (continued): The hazard is related to the rate of change in survival. For the Natality teaching dataset, the hazard function (solid line) for preterm birth and the corresponding survival function (dashed line) are shown in Figure 7.3. The hazard function is near 0 at times when the survival function is relatively flat (few events) and is greater when the survival function is steeper (events occurring more frequently). In this teaching dataset, the hazard of preterm birth is near 0 through around gestational age 21 weeks and there is a marked increase in hazard after around 28 weeks.

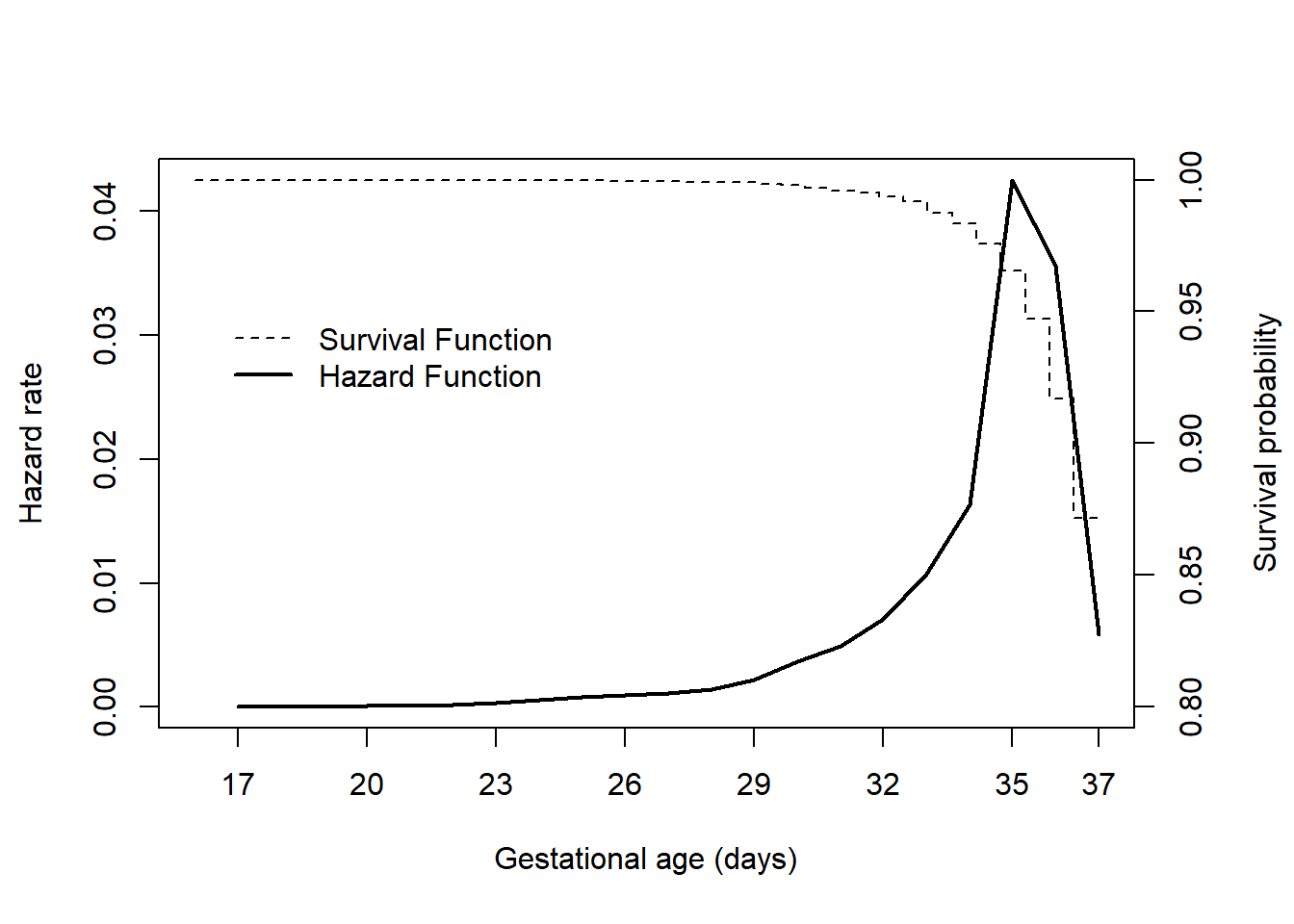
Figure 7.3: Hazard function for time to preterm birth data